2773

считаем, что эта масса сосредоточена в центре масс прямоугольника (совпадает с его центром) с координатами

111

5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

Если функция f(x) непрерывна на отрезке a, b и

известна еѐ первообразная F(х), то определѐнный интеграл можно вычислить по формуле Ньютона-Лейбница:

a

Однако во многих случаях первообразная функция F(x) не выражается через элементарные или находится слишком сложно. Поэтому возникает задача о приближѐнном вычислении интеграла.

Численные методы приближѐнного вычисления интеграла основаны на приближѐнном представлении определѐнного интеграла интегральной суммой I n или

величиной, близкой к I n : b

f (x)dx I n .

a

5.I. Формулы прямоугольников b

Пусть надо вычислить f (x)dx . Разобьѐм отрезок a, b

x0 a, x1, x2 ,... xn b . Вычислим значения функции f(x) в этих точках:

y0 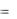f (a); y1 f ( x1 );... yk f ( xk );... yn 1 f ( xn 1 ); yn f (b)

.

Составим две суммы:

112

даѐт значение интеграла с недостатком, а (3) – с избытком.

более точных способах вместо интегральных сумм рассматривают суммы другого вида.

5.2. Формула трапеций

заменим соответствующей хордой, в результате чего криволинейная трапеция заменяется суммой площадей элементарных прямоугольных трапеций. Геометрически очевидно, что такие трапеции более точно выражает искомую площадь, чем прямоугольники. Площадь каждой элементарной трапеции равна:

114

5.3. Формула парабол (формула Симпсона)

Ещѐ большая точность получается, если элементарные криволинейные трапеции заменить параболическими трапециями.

Разобьѐм отрезок [a,b] на чѐтное число n 2m равных

точки, не лежащие на одной прямой, можно провести единственную параболу второй степени:

Через выделенные тройки точек проведѐм параболы с осями, параллельными оси Оу. Площадь элементарной криволинейной трапеции заменится площадью элементарной параболической трапеции. Вычислим площадь такой трапеции.

Лемма: Площадь параболической трапеции с основанием

Доказательство.

Положение начала координат на оси Ох не влияет на величину площади, поэтому выберем начало координат в середине отрезка. Тогда

116

Рис. 53.

A( h, y0 ); A1 (0, y1 ); A2 (h1 , y2 ) .

Учитывая (5), имеем:

Исключим коэффициенты а и с. Так как A0 , A1 и A2 лежат на

параболе, то их координаты удовлетворяют уравнению параболы:

y0 ah2 bh c

h

Следовательно, S 3 ( y0 4 y1 y2 ) ч.т.д.

Запишем эту формулу для каждой элементарной параболической трапеции:

117

Это число принимают за приближѐнной значение интеграла:

погрешность формулы Симпсона оценивается следующим

Все рассмотренные формулы тем точнее, чем больше n:

R0 при n 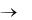. При одном и том же n формула Симпсона

–наиболее точная из них.

Пример. Вычислить приближенно

118

БИБЛИОГРАФИЧЕСКИЙ CПИСОК

1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1985. Т.1. 432 с.

2.Толстов Г.П. Элементы математического анализа. М.:

Наука, 1974. Т.1. 520 с.

3.Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: Наука, 1975. 624 с.

4.Слободская В.А. Краткий курс высшей математики.

М.: Высшая школа, 1969.

5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Учеб. пособие для студентов втузов. М.: Высшая школа, 1996. Ч. 1.

120