Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2773

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.27 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

		n	1	n	1
lim	0		f ( k ) xk		g( k ) xk
max xk	0	k	0	k	0
		k	0	k	0
b		b
f (x)dx			g(x)dx.
a		a

Замечание: Свойство справедливо для любого конечного числа слагаемых.

Следствие:

Af (x) Bg(x) dx A f (x)dx B g(x)dx

(свойство линейности операции интегрирования).

3. Если отрезок a, b разбит точкой С на части, то

интеграл по всему промежутку равен сумме интегралов по его частям (при любом расположении точек a, b, и с).

b	c	b
f (x)dx	f (x)dx	f (x)dx
a	a	c

(свойство аддитивности).

Доказательство:

а) Пусть a<c<b. Величина определѐнного интеграла не зависит от способа деления отрезка a, b на частичные. Будем разбивать отрезок a, bна части так, чтобы точка с оказалась одной из точек деления в каждой из интегральных сумм.

Рис. 11.

f (x)dx

lim

f ( k )

max

lim

f (

k )

f ( k ) xk

max

lim

f (

k )

lim

f (

k ) xk

max

(a,c)

max xk

(c,b)

f (x)dx

f (x)dx.

Геометрически: SaABb

SaACc

ScCBb .

b) Если a<b<c, то по доказанному:

c	c	b	b	c	c	b	c	b
								.
a	a	c	a	a	b	a	a	c

II. Свойства, выражаемые неравенствами

1. Если функция		f (x)		0 интегрируема на отрезке a, b
b
(a<b), то	f (x)dx	0 .
a
Доказательство:
b			n 1
f (x)dx	lim	0		f ( k ) xk .
a	max xk	0	k	0
a			k	0

Каждое слагаемое интегральной суммы In неотрицательно,

поэтому I n 0 .	Предел неотрицательной величины не может
быть отрицательным.
2. Если f(x) и g(x) интегрируемы на отрезке a, b					(a<b) и
удовлетворяют на нѐм равенству f (x)			g(x) , то
b	b
f (x)dx	g(x)dx (неравенства можно интегрировать,
a	a
когда a<b).
Доказательство:
Так как g(x) f (x) 0		x a,b , то по свойству 1:
b		b	b
g(x) f (x) dx 0		g(x)dx	f (x)dx 0
a		a	a
b	b
и f (x)dx	g(x)dx .
a	a
Неравенство обращается в равенство, если				f (x)	g(x) на
a, b .
3. Если f(x) интегрируема на отрезке a, b				и a<b, то

	b		b
								(6)
		f (x)dx		f (x)	dx			(6)
	a		a
Доказательство:
	n	1		n	1
	n	1		n	1
		f (xk ) xk				f (xk )	xk (правило	треугольника).
		f (xk ) xk				f (xk )	xk (правило	треугольника).
	k	0		k	0
Переходя в			обеих частях неравенства к					пределу при
max xk		0 получим формулу (6).
4.		Если	функция f(x) интегрируема на					a, b (a<b) и
существуют числа m и М такие,							что во всех точках отрезка

a, b выполняется неравенство m f (x)

M , то

m(b a)

f (x)dx M (b a) .

Рис. 12.

Геометрический смысл:

SaCDb SaABb SaC1D1b (рис. 12).

Доказательство:

По свойству 2 проинтегрируем неравенство:

f (x)

M по отрезку a, b .

mdx

f (x)dx

Mdx

или

f (x)dx

dx,

m(b a)

f (x)dx M (b a).

Пример. Оценить интеграл:

1 sin2 x

Так как

a,b ,

sin2

то

1,12 .

2 2

5. Теорема о среднем для определѐнного интеграла.

Теорема. Если функция f(x) непрерывна на отрезке a, b , то внутри отрезка найдется хотя бы одна точка с c a, bтакая, что имеет место равенство:

y
	B
M	B	b
M		b

						f(c)	f (x)dx	f (c)(b a)	(7)
						f(c)
m	A						a
m
0


		a		c	b	x
		a		c	b	x

			Рис. 13.
	Геометрический смысл. Если							обе части	равенства

рассматривать как площади фигур, то криволинейная трапеция aABa равновелика прямоугольнику с длиной основания (b-a) и

высотой f(c).
	Доказательство:
	А)	Пусть a<b. По теореме Вейерштрасса,					непрерывная
на	отрезке		a, b	функция f(x) достигает		на	нѐм своего
наибольшего			М	и	наименьшего	m	значений:
m	f (x)	M	x	a,b .	Интегрируем это	неравенство в

пределах от а до b; по свойству 4 получим: b

m(b a) f (x)dx M (b a) .

								a
Делим на (b-a)>0:
		1				b
m		1						f (x)dx M .

			b		a
			b		a
						a
					1		b
Обозначим	h				1			f (x)dx . Тогда	m	h M . Так как

				b	a
				b	a
							a
функция f(x)		непрерывна на отрезке a, b ,								то она принимает
								66

любое промежуточное значение, заключѐнное между m и М.

Поэтому h – одно из значений функции f(x) на a,b :							f (C) h ,
					1		b
где	C	a,b ,	т.е.	f (c)	1		f (x)dx


					b	a
							a
(8)
		b
	или	f (x)dx	f (c)(b a)
		a
	в) Пусть a>b. Тогда
	b	a
	f (x)dx	f (x)dx	(a b) f (c)	(b a) f (c)
	a	b

получим интеграл, где нижний предел меньше верхнего. Число f(c), получаемое по формуле (8), называется средним значением функции на отрезке a, b .

Пример.

Сила переменного

тока равна i

I0 sin

2 t

Найти среднее значение i 2 (t)

за период Т:

i (t)

i (t) 0. i 2 (t)

i 2 (t)dt

I 0

2 T

2 2 t

I 0 2

sin

t t

2 (t)

Рис. 14.

эф

3.4. Определѐнный интеграл с переменными верхним пределом. Связь между определѐнным и неопределѐнным интегралом

Пусть функция f(x) интегрируема на отрезке	a, b . Тогда
b
f (x)dx есть число, не зависящее от	переменной

интегрирования. Поэтому в определѐнном интеграле переменную интегрирования можно обозначить любой буквой:

b	b	b
f (x)dx	f (t)dt	f (z)dz	S	(если	f (x)	0 ).
a	a	a
Рассмотрим отрезок		a, x , где	a	x b .	Раз функция
интегрируема на a, b ,		то она интегрируема на				a, x , но на

этом отрезке верхний предел интегрирования будет переменным:

f (x)dx

f (t)dt .

y=f(x)

f(c)

x+ x

Рис. 15.

При

этом

каждому

значению

a,b соответствует

единственное значение определѐнного интеграла. Таким образом интеграл с переменным верхним пределом есть функция верхнего предела:

	x
Φ(x)	f (t)dt a	x b .	(9)
	a
(При f (x) 0	Φ(x) можно	рассматривать как	площадь

заштрихованной криволинейной трапеции).

Теорема. Если функция f(x) непрерывна на отрезке a, b , то функция Φ(x) дифференцируема на a, b , причѐм

Φ (x) 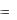f (x) .

Т.е. Φ(x) есть первообразная для f(x) на a, b . Производная

от определѐнного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой

аргумент t заменяется на х:

f (t)

t x

f (x) .

Доказательство.

Фиксируем х

a,b

и найдѐм приращение

функции Φ(x) :

Φ(x)

f (t)dt

Применяем теорему о среднем к отрезку

x, x

x :

Φ(x) f (c) x ,

c x, x

x .

(10)

Так как при x

x ,

то и

0 .

Φ(x)

Разделим обе части (10) на x : f (c) . По условию x

f(x) непрерывна на		a, b ,	поэтому	lim		f (c)	f ( x) .
				c	x
				x	0
Значит, существует предел левой части (10) при						x	0 :
lim	Φ(x)	f (x) , т.е.	Φ (x)	f (x) .

	x
x 0	x

Таким образом, функция Φ(x) является первообразной для f(x), непрерывной на a, b . Поэтому можно записать:

		x
f (x)dx	Φ(x) C или, так как Φ(x)	f (t)dt , то
		a
	x
f (x)dx	f (t)dt C	(11)
	a

Формула (11) устанавливает связь между неопределѐнным и определенным интегралами.

3.5. Формула Ньютона-Лейбница. Вычисление определѐнного интеграла

Установленная связь между определѐнным и неопределѐнным интегралами (11) позволяет получить очень важную формулу для вычисления определѐнного интеграла.

Теорема. Если функция f(x) непрерывна на отрезке a, b и F(x) есть какая-то из первообразных для f(x) на a, b , то имеет место формула:

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.24 Mб02761.pdf
#
15.11.20222.24 Mб02763.pdf
#
15.11.20222.24 Mб22764.pdf
#
15.11.20222.24 Mб22765.pdf
#
15.11.20222.25 Mб02768.pdf
#
15.11.20222.27 Mб02773.pdf
#
15.11.20222.28 Mб22777.pdf
#
15.11.20222.28 Mб02780.pdf
#
15.11.20222.29 Mб02784.pdf
#
15.11.20222.29 Mб12787.pdf
#
15.11.20222.3 Mб02788.pdf