
2160
.pdf
А2 |
|
А2 |
i2 |
По окружности |
|
|
|
|
x |
i1 |
По прямой |
|
||
|
|
А1


 А1
А1
Рис. 35. Вращение точки вокруг неподвижной оси
Истинные размеры фигуры общего положения не могут быть определены вращением ее вокруг одной оси: 1) вращением вокруг проецирующей прямой фигуру приводят в положение проецирующей плоскости ( ), а затем 2) вращением вокруг второй проецирующей прямой – в положение (//) параллельное плоскости проекций.
Плоскость фигуры перпендикулярна фронтальной плос-
кости проекций, если горизонталь этой фигуры |
фронталь- |
|
ной плоскости проекций h2 |
2 . |
|
Чтобы произвольно расположенную плоскость перезадать во фронтально-проецирующую, за ось вращения следует принять горизонтально-проецирующую прямую.
Чтобы произвольно расположенную плоскость перезадать в горизонтально-проецирующую, за ось вращения следует принять фронтально-проецирующую прямую.
Способ замены плоскостей проекций
Для упрощения решения задач можно использовать второй путь: фигуру оставить на месте и ввести новые плоскости проекций.
40
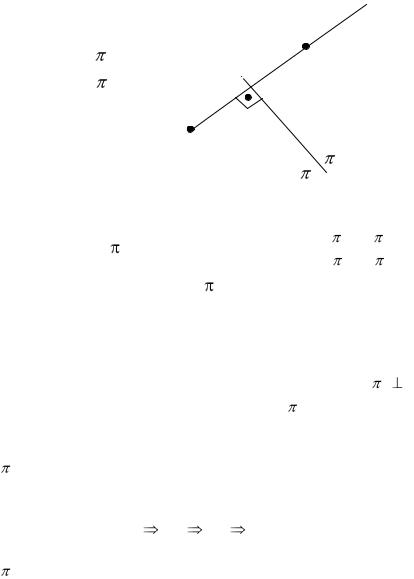
На эпюре Монжа это выглядит следующим образом
(рис. 36).
А2 
// |
А3 |
2 |
// |
|
|
1 |
|
А1 |
|
3
1
Рис. 36. Преобразование комплексного чертежа точки методом замены плоскостей
Плоскость |
1 |
является общей для двух систем |
2 |
и |
3 |
. |
|
|
|||||
|
1 |
|
1 |
|
||
|
|
|
|
|||
Расстояние от т. A2 до 1 одинаковое в обеих системах. Пример 8. Определить натуральную величину треуголь-
ника общего положения. |
|
|
|
|
Решение |
|
|
|
|
1.Проведем горизонталь (рис. 37). |
|
|
|
|
Введем дополнительную плоскость проекций |
3 |
го- |
||
|
|
|
|
|
ризонтали. Проекция треугольника на |
3 |
превращаются в |
||
|
|
|
|
|
прямую линию. |
|
|
|
|
2. Вводим дополнительную |
плоскость |
проекций |
||
4// A3C3 .
3.Определим проекции произвольной точки K на натуральном изображении треугольника:
K 4 |
K3 K1 K 2 . |
4. Вводим |
дополнительную плоскость проекций |
4 // A3C3 . |
|
41

5. Определим проекции произвольной точки K на натуральном изображении треугольника:
K 4 K3 K1 K 2 .
Рис. 37. Решение примера 8
Метод плоско-параллельного перемещения
При параллельном перемещении (переносе) справедливо утверждение, которое может быть выражено следующей теоремой: при параллельном переносе геометрической фигуры относительно плоскости проекций проекция фигуры на эту
42
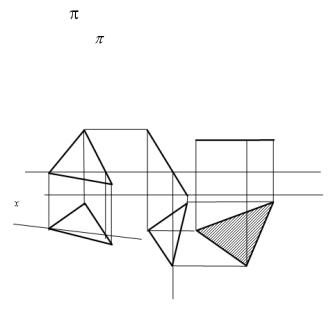
плоскость хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.
Пример 9. Определить натуральную величину треугольника общего положения методом плоско-параллельного перемещения.
Решение
1.Вводим горизонталь (рис. 38).
2.Переносим треугольник в параллельной плоскости так, чтобы горизонталь стала перпендикулярно оси x . 3.Разворачиваем полученную проекцию параллельно
плоскости 1 .
На плоскости 1 получили натуральную величину за-
данного треугольника.
Данный метод отличается от метода вращения тем, что 1) не надо показывать ось вращения; 2) более компактное расположение на поле чертежа.
Рис. 38. Решение примера 9
2.13. Многогранники
Задачу по определению сечения многогранника сводят к задаче пересечения прямой с плоскостью (способ граней) или к задаче пересечения прямых (способ ребер).
43
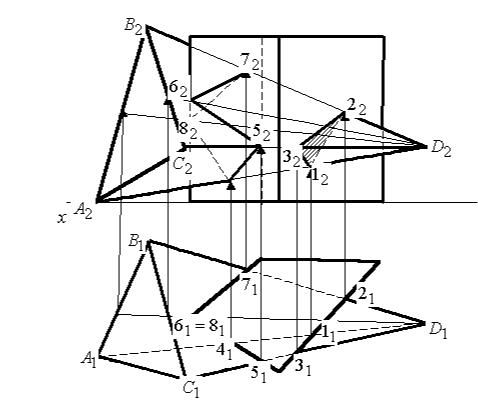
Пример 10. Построить пересечение прямой призмы и наклонной пирамиды.
Решение
Точки 1, 2, 3 находим как пересечение ребер с гранью призы. Получим сечение 123 (рис.39).
7
Рис. 39. Решение примера 10
44
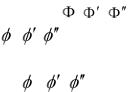
2.14. Пересечение тел вращения
Способ секущих сфер
При построении линии пересечения двух поверхностей способом вспомогательных секущих плоскостей секущие плоскости могут быть как общего, так и частного положения. Наиболее широкое применение находят плоскости частного положения.
Решение задачи построения линии пересечения двух поверхностей этим способом рассмотрим на пример пересечения цилиндра с полусферой.
Пример 11.
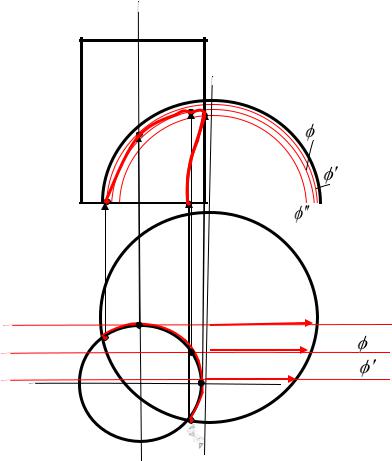
Построить пересечение поверхности цилиндра с полусферой (рис.40).
Решение
Сначала на проекциях отметим очевидные общие точки (1, 2). Затем вводим вспомогательные плоскости частного по-
ложения – фронтальные , , . Они пересекают |
фигуры |
|
по параллелям |
1, 1, 1 . На фронтальной проекции |
вспомо- |
гательные плоскости пересекают сферу в виде концентрических окружностей 2 , 2 , 2 . На пересечении этих окружно-
стей и восстановленных из точек горизонтальной проекции цилиндра находятся точки пересечения поверхностей (3, 4, 5). Полученные точки соединяем плавной кривой.
45
51
52 |
42 |
2 |
|
|
2
x |
12 |
1 |
32 |
|
21 |
|
|
2 |
2 |
1 |
|
|
||
|
1 |
|
|
|
|
|
31 |
|
1 |
|
|
|
|
|
|
|
41 |
|
1 |
|
|
|
|
|
Рис. 40. Решение примера 11
46
Способ концентрических сфер
Для пересечения поверхностей вращения, особенно соосных, в качестве вспомогательных поверхностей используют сферы, соосные данным поверхностям.
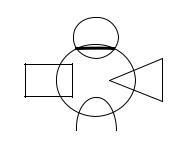
Если тела вращения пересекают сферу и их оси симметрии проходят через центр сферы, то проекции линий пересечения (окружности) проецируются в прямые линии (рис.41).
Рис. 41. Пересечение сферы различными телами вращения
Для того, чтобы применить этот метод, необходимо убедиться в том, что оси поверхностей – пересекающиеся прямые – параллельны одной из плоскостей проекций, т.е. имеется общая ось симметрии и способ секущих плоскостей не применим, т.к. они не дают графически простых линий на поверхности.
Решение задачи построения линии пересечения двух поверхностей этим способом рассмотрим на примере пересечения усеченного конуса с конусом.
Пример 12.
Построить пересечение поверхности усеченного конуса с конусом (рис. 42).
Решение
Центр вписанных концентрических сфер O лежит на
47

|
11 |
2 |
31 |
|
|
|
41 |
|
12 |
x |
|
|
O1 |
|
21 |
O2 |
42 |
32 |
|
Рис. 42. Метод сфер |
|
пересечении осей конусов. Сначала определяем точку 1 с rmin , затем т. 2 с rmax . Далее промежуточные точки 3 и 4, которые
лежат на пересечении окружностей вписанных промежуточных сфер. Соединив их плавной кривой, получим линию пересечения поверхностей.
48
3. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Рекомендации к решению задач
Перед тем приступить к решению задач необходимо ответить на теоретические вопросы, которые охватывают основные положения курса начертательной геометрии.
•Какими способами в пространстве задаются прямая, плоскость?
•Как разделить отрезок прямой в заданном отношении или на несколько равных частей с помощью чертежных инструментов не прибегая к вычислениям?
•Какие прямые называются параллельными, пересекающимися, скрещивающимися?
•Каковы отличительные признаки плоских фигур: треугольника, трапеции, параллелограмма, ромба, прямоугольника, квадрата, окружности?
•Какой треугольник называют равнобедренным, равносторонним, прямоугольным?
•Как построить в треугольнике высоту, медиану, биссектрису угла?
•Какими свойствами обладают высоты, медианы, биссектрисы углов в равнобедренном, равностороннем треугольниках?
•Какие построения выполняют для определения центра вписанной в треугольник или описанной вокруг него окружности?
•Какими свойствами обладают диагонали параллелограмма, ромба, высоты равнобедренной трапеции, проведенные из еѐ вершин к основаниям?
•Как построить плоский многоугольник, равный заданному?
•Как построить точку, принадлежащую какой-либо плоскости?
49
