Виброакустическая диагностика технических объектов

Следует отметить, что при суммировании хотя бы пяти-шести гармонических колебаний с взаимно независимыми частотами получается процесс, практически неотличимый от случайного, близкого к нормальному [4]. Следовательно, при достаточно большом числе гармоник почти периодический процесс приобретает все свойства случайного.

Еще одним примером непериодических установившихся колебаний являются почти гармонические, модулированные по амплитуде, частоте и (или) фазе непериодическими функциями времени. Такие колебания могут иметь не только непрерывный, но и дискретный спектр. К непериодическим колебаниям относятся также сравнительно короткие отрезки периодических колебаний, в частности, участок моногармонического процесса, и переходные (неустановившиеся) колебания, например, затухающие или нарастающие во времени процессы; импульсы или последовательность нескольких импульсов самой разнообразной формы: типа скачка, прямоугольной, колоколообразной и др. В последнем случае непрерывный спектр одиночного импульса и огибающая дискретного спектра периодической последовательности, полученной путем повторения этого импульса, совпадают по форме. С увеличением числа импульсов нагружения системы с определенной их последовательностью непрерывный спектр в сигнале все более расщепляется и в пределе принимает дискретную структуру.

Переходным называется детерминированный или случайный процесс, имеющий конечную длительность.

3.2.4. Классификация случайных процессов

Большинство колебательных процессов, с которыми приходится встречаться на практике, носят в той или иной степени случайный характер, при этом текущие значения процесса могут быть определены лишь с некоторой вероятностью. Случайный колебательный процесс может быть представлен совокупностью статистических характеристик, постоянных или переменных во времени.

Как указывалось ранее, процесс, описывающий случайное физическое явление, нельзя задать явной математической зависимостью, поскольку каждое наблюдение этого явления дает невоспроизводимый результат.

Другими словами, любое наблюдение дает только один вариант из множества возможных. Рассмотрим, например, напряжение на выходе генератора теплового шума как функцию времени. Фиксируя временные реализации сигнала в различные моменты времени, получим различные реализации зависимости напряжения от времени (рис. 3.7).

Конкретная реализация процесса, описывающего случайное явление, называется выборочной функцией (или реализацией, если речь идет о наблюдении конечной длительности). Совокупность всех возможных выборочных

61

функций, которые может дать случайное явление, называется случайным или стохастическим процессом. Таким образом, под реализацией случайного явления понимается один из возможных исходов случайного процесса.

Рис. 3.7. Выборочные функции на выходе генератора теплового шума:

а) Т + ∆t; б) 2Т + ∆t; в) 3Т + ∆t

Случайные процессы делятся на стационарные и нестационарные. В свою очередь стационарные случайные процессы – на эргодические и неэргодические (рис. 3.8).

Рис. 3.8. Классификация случайных процессов

Дальнейшая классификация нестационарных случайных процессов проводится по особенностям их не стационарностей.

62

3.2.4.1. Стационарные случайные процессы

Если физическое явление описывается случайным процессом, то свойство этого явления в принципе можно оценить в любой момент времени путем усреднения по совокупности выборочных функций, образующих случайный процесс. Рассмотрим, например, совокупность выборочных функций (называемую также ансамблем) (рис. 3.9), определяющую случайный процесс.

Рис. 3.9. Ансамбль реализаций, задающих случайный процесс

Среднее значение (первый момент) этого случайного процесса в момент времени t1 можно вычислить, взяв мгновенные значения всех выборочных функций ансамбля в момент времени t1, сложив эти значения и разделив на число выборочных функций.

Следовательно, среднее значение µx (t1) случайного процесса {x(t)}, где символ {} обозначает ансамбль выборочных функций, определяется формулой

в которой суммирование производится в предположении равновероятности всех выборочных функций.

В общем случае, когда µx(t1), определенное уравнением (3.12), зависит от момента времени t1, случайный процесс {x(t)} называется нестационарным. В том частном случае, когда µx(t1) не зависит от момента времени t1,

случайный процесс называется слабостационарным или стационарным в широком смысле. Среднее значение слабостационарного процесса постоянно, а ковариационная функция зависит только от сдвига времени t.

Свойство инвариантности статистических характеристик относительно произвольного момента времени используется для классификации случайных колебательных процессов. Все статистические характеристики случайного стационарного колебательного процесса инвариантны по отношению к моменту времени.

63

Таким образом, случайный стационарный процесс есть ансамбль реализаций, статистические свойства которого инвариантны по отношению к переносу начала отсчета времени. Случайные стационарные колебания служат удобной моделью реальных процессов, свойства которых достаточно медленно изменяются во времени.

Случайный процесс называется стационарным в широком смысле, если его среднее значение постоянно (не зависит от времени), а автокорреляция зависит только от временного сдвига. Обычно при определении среднего значения, корреляции и спектральной плотности мощности случайного процесса используют статистическое усреднение по ансамблю. Однако на практике обычно не удается получить ансамбль реализаций требуемого процесса, по которому можно было бы вычислить эти статистические характеристики. Желательно оценивать все статистические свойства по одной выборочной реализации x(t), заменяя усреднение по ансамблю усреднением по времени. Свойство, позволяющее такую замену осуществить, называют эргодичностью.

В общем случае для определения полного набора функций распределения, задающих структуру случайного процесса {x(t)}, нужно вычислить бесконечное число моментов и смешанных моментов высших порядков. В том случае, когда все моменты и смешанные моменты инвариантны во времени, случайный процесс {x(t)} называется строгостационарным или стационарным в узком смысле. Во многих приложениях проверка слабой стационарности позволяет обосновать строгую стационарность.

3.2.4.2. Эргодические случайные процессы

Определить характеристики случайного процесса можно путем усреднения по ансамблю в определенные моменты времени. Возьмем, например, k-ю выборочную функцию ансамбля (см. рис. 3.9). Среднее значение µx(k), вычисленное по k-й реализации, определяется выражением (3.12).

Если случайный процесс {x(t)} стационарен, а µx(k), вычисленное по различным реализациям согласно формуле (3.12), совпадают, то случайный процесс называется эргодическим. Для эргодических процессов средние значения, полученные усреднением по времени (как и другие характеристики, вычисленные усреднением по времени), равны аналогичным характеристикам, найденным усреднением по ансамблю, т.е. µx(k) = µx. Свойством эргодичности могут обладать только стационарные процессы.

Стационарный процесс будет эргодическим, если его статистические характеристики, полученные усреднением по ансамблю, с вероятностью, близкой к единице, равны тем же характеристикам, полученным усреднением по времени из любой достаточно длинной реализации случайного процесса. При нарушении этого условия колебательный процесс будет неэргодическим.

64

Другими словами, эргодическим называется случайный стационарный процесс, для которого результаты усреднения по времени в пределах отдельной реализации одинаковы для всех реализаций. Таким образом, усреднение по времени для любой отдельной реализации эквивалентно соответствующему усреднению по ансамблю реализаций.

Очевидно, что случайные эргодические процессы образуют очень важный класс случайных процессов, поскольку все свойства эргодических процессов можно определить по единственной выборочной функции. На практике случайные стационарные процессы обычно оказываются эргодическими. Именно по этой причине свойства случайных стационарных явлений часто можно определить по одной наблюдаемой реализации. Для любой реализации xk(t) случайного стационарного процесса {xk (t)}, где k = 1,2,3,... – номер реализации, средний квадрат определяется равенством

Для эргодического процесса результат выборки не должен зависеть от ее номера (k) и будет одним и тем же для всех реализаций. Соответствующее среднее по ансамблю значение определяется равенством

и в случае стационарного процесса не зависит от t. Для эргодического процесса оба усреднения дают одинаковый результат.

В общем случае результаты усреднения по любой отдельной реализации процесса не характеризуют свойство ни одной из его реализаций, поскольку информация о зависимости свойств процесса от времени в результате такого усреднения утрачивается.

Принято считать, что случайный процесс эргодичен, если с вероятностью, равной единице, все его статистические характеристики можно предсказать по одной реализации из ансамбля с помощью усреднения по времени. Иными словами, средние значения по времени почти всех возможных реализаций процесса с вероятностью единицы сходятся к одной и той же постоянной величине – среднему значению по ансамблю.

3.2.4.3. Нестационарные случайные процессы

Необходимо заметить, что в общем случае строго стационарных процессов в природе нет. Считать процесс стационарным или нестационарным, зависит в основном от выбора продолжительности времени наблюдения.

К нестационарным процессам относятся все случайные процессы, неудовлетворяющие условиям стационарности. Если не наложены дополнительные ограничения, то свойства случайных нестационарных процессов

65

обычно зависят от времени и могут быть установлены только путем усреднения в отдельные моменты времени по ансамблю выборочных функций, образующих процесс. На практике часто не удается получить достаточное для точной оценки свойств процесса число реализаций. Этим фактом объясняется отставание в развитии практических методов измерения и анализа случайных нестационарных процессов.

Во многих случаях случайные нестационарные процессы, отвечающие реальным физическим явлениям, имеют особенности, упрощающие их анализ и измерение. Так, большой класс случайных нестационарных колебательных процессов, у которых хотя бы одна статистическая характеристика зависит от времени, можно представить в виде суммы

где x(t) – случайный стационарный процесс; µ(t) и xс(t) – неслучайные функции времени, причем x(t) является математическим ожиданием x(t).

Случайные колебания со слагаемым хс(t) в виде детерминированной функции времени и при µ(t) = 1 относятся к нестационарным по математическому ожиданию колебательным процессам. Обычно детерминированная составляющая xс(t), называемая трендом, рассматривается как нежелательная компонента, искажающая наблюдения. Для исключения тренда используются специальные методы фильтрации и сглаживания [11]. Если xс (t) рассматривается как помеха, а x(t) – как полезный сигнал, то такие помехи

иногда называют аддитивными, т.е. суммируемыми с сигналом. Колебательный процесс, нестационарный по дисперсии, определяется формулой (3.15) при условии, что xс(t) = const, а µ(t) – детерминированная функция времени. Такие случайные процессы иногда называют мультипликативными. Процессы, нестационарные по спектральной плотности (корреляционной функции), изменяют свои частотные свойства во времени, а колебательные процессы, нестационарные по одномерной плотности распределения, изменяют во времени свои законы распределения. Кроме указанных, возможны колебательные процессы с более сложными видами нестационарности, а также комбинированные нестационарные процессы.

Нестационарным называется любой процесс, не обладающий свойством стационарности. Статистические характеристики такого процесса, определенные усреднением по ансамблю его реализаций, не являются инвариантными по отношению кпереносу начала отсчета навременной оси и зависят от времени.

Другими словами, данные представляются случайным нестационарным процессом, если все выборочные функции которого имеют общий детерминированный тренд. Если случайный нестационарный процесс имеет такой вид, то для описания его свойств не всегда требуется усреднение по ансамблю. Иногда многие важные свойства удается оценить по единственной выборочной функции, как и в случае эргодических стационарных процессов.

66

4. ОБРАБОТКА ВИБРОСИГНАЛА

4.1. Фильтрация

Традиционный метод определения частотного спектра электрического сигнала заключается в фильтрации последнего аналоговыми полосовыми фильтрами с различными средними частотами (или одним полосовым фильтром с перестраиваемой в определенном диапазоне средней частотой) и в измерении присущей отдельным частотным полосам пропущенной мощности. Хотя сказанное относится именно к анализу в полосах с постоянной абсолютной шириной, осуществляемый при помощи фильтров (в том числе цифровых фильтров) анализ имеет определенные преимущества, в частности при анализе в полосах с постоянной относительной шириной. Сигнал на выходе фильтра с фиксированной средней частотой полосы пропускания является результатом свертки поступающего на его вход сигнала и импульсной характеристики (передаточной функции) фильтра.

В частотной области этому соответствует перемножение соответствующих (комплексных) частотных функций. Следовательно, спектр амплитуды сигнала на выходе из фильтра равен произведению спектров амплитуды соответственно сигнала на входе и спектральной характеристики фильтра. Аналогичным образом, спектр мощности сигнала на выходе равен произведению соответствующих спектров мощности (рис. 4.1). Отметим, что процесс фильтрации обусловливает изменения фазовых соотношений составляющих сигнала. Однако фазовые изменения вообще не сказываются на пропускаемой фильтром мощности.

Рис. 4.1. Спектры амплитуды и мощности претерпевшего фильтрацию сигнала

67

На рис. 4.2 показана упрощенная блок-схема несложной анализирующей системы. Чтобы определить спектр анализируемого сигнала, надо знать, как изменяется средняя частота используемого фильтра в подлежащем анализу диапазоне частот сигнала. Скорость, с которой могут происходить изменения средней частоты полосы пропускания, зависит от временной задержки, обусловливаемой отдельными устройствами анализирующей системы, т.е. фильтром, детектором и отсчетным или регистрирующим устройством.

Рис. 4.2. Принципиальная блок-схема анализатора с полосовыми фильтрами

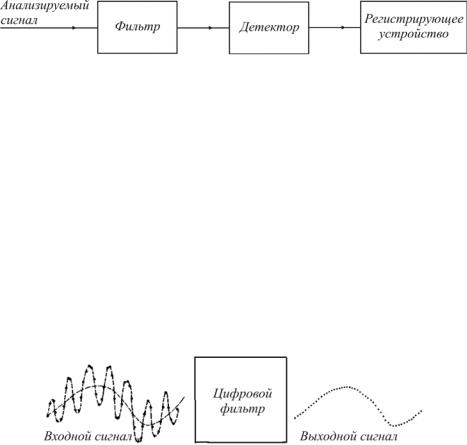
В классических анализирующих системах, нашедших широкое применение на практике, все упомянутые выше устройства были аналоговыми, но происшедший в последние годы технический прогресс привел к все более широкому использованию цифровых фильтров и детекторов. В аналогоцифровых преобразователях подлежащий анализу сигнал уже во входном блоке подвергается аналого-цифровому преобразованию, в результате которого получается числовой ряд дискретных значений в интервале времени измерения сигнала. Дискретные значения (численный ряд) анализируемого сигнала обрабатываются цифровым фильтром, изменяя его определенным образом и создавая новый численный ряд, который отображает данные профильтрованного определенным образом сигнала (рис. 4.3). По существу, при обсуждении цифровых фильтров будут рассматриваться лишь так называемые «рекурсивные цифровые фильтры».

Рис. 4.3. Дискретное представление сигналов на входе и выходе цифрового фильтра

В отличие от быстрого преобразования Фурье, при котором одновременно обрабатываются определенные блоки данных, рекурсивная цифровая фильтрация является непрерывным процессом, в котором отдельным входным данным придаются соответствующие выходные данные. В этом смысле рекурсивная цифровая фильтрация аналогична аналоговой фильтрации. По

68

существу, можно создать рекурсивные цифровые фильтры, параметры которых аналогичны параметрам любых практических фильтров или даже фильтров, которые нельзя реализовать в аналоговой форме.

Однако упомянутые последними цифровые фильтры обычно имеют неприемлемые свойства, и поэтому их более подробное рассмотрение не предусмотрено. Следовательно, основная часть излагаемого в данной главе материала будет относиться как каналоговым, таки цифровым методам фильтрации.

4.1.1. Фильтры

Основным параметром полосового фильтра является ширина его полосы пропускания и ее зависимость от частоты. Важное различие имеется между фильтрами с постоянной абсолютной и постоянной относительной (процентной) шириной полосы пропускания. Абсолютная ширина полосы пропускания фильтра с постоянной относительной (процентной) шириной является постоянной процентной долей средней частоты этой полосы. На рис. 4.4, иллюстрирующем это важное различие, графически сопоставлены полосы с постоянной абсолютной и постоянной относительной шириной, причем на горизонтальной оси отложена как линейная, таки логарифмическая шкала частоты.

Постоянная ширина полосы пропускания обеспечивает идентичное разрешение по частоте при применении линейной шкалы частоты. Это способствует, например, выделению гармонических составляющих и обнаружению гармонической структуры исследуемых сигналов (рис. 4.5). Однако линейная шкала частоты автоматически ограничивает ширину перекрываемого при практическом анализе диапазона частот. На практике этот диапазон обычно перекрывает одну или по крайней мере две декады (см. рис. 4.4).

С другой стороны, постоянная относительная (процентная) ширина полосы пропускания обеспечивает идентичное разрешение по частоте при применении логарифмической шкалы частоты и, следовательно, эффективна при анализе в широком, т.е. перекрывающем 3 или больше декад, диапазоне частот. Другое преимущество постоянной относительной ширины полосы пропускания заключается в ее соответствии постоянному значению добротности Q, т.е. постоянному значению коэффициента усиления в области резонансных пиков (рис. 4.6). Следовательно, при определении спектров, в которых доминирующими являются резонансы конструкции или системы, целесообразно и эффективно использовать логарифмическую шкалу частоты и фильтр с постоянной относительной шириной полосы пропускания. Разумеется, что ширина полосы пропускания используемого фильтра должна быть меньше ширины самого узкого резонансногопика анализируемого сигнала.

К другим поводам для применения логарифмической шкалы частоты (но не всегда фильтров с постоянной относительной шириной полос пропускания) относятся:

69

70