Виброакустическая диагностика технических объектов

Рис. 4.21. Временные задержки в процессе определения присущих максимумам и минимумам спектров значений при текущем линейном и экспоненциальном (RС) усреднении

Приведенные зависимости на рис. 4.20 позволяют оценить соответствующие значения временной задержки, которые необходимо учитывать при разработке конверторов, использующих линейное или экспоненциальное усреднение. По показанным на рис. 4.21 кривым можно оценить временную задержку, относящуюся к наклонным участкам получаемых в результате частотного анализа спектров. Отметим, что на рис. 4.21 также показан присущий усреднению с помощью простой RС-схемы асимптотический предел 8,7 дБ/2RС, который соответствует максимальной скорости спада уровня отдаваемого детектором сигнала и на практике часто ограничивает скорость развертки частоты при анализе.

4.3. Модуляция колебаний

Все сигналы во временной области были представлены суммами гармонических колебаний с фиксированными значениями амплитуды и частоты. По существу главная цель анализа Фурье заключается в выделении и определении этих фиксированных частот.

Модулированный сигнал часто наиболее удобно представить при помощи одного колебания с изменяющимися во времени амплитудой и «мгновенной частотой» [14]. Разумеется, что при представлении модулированного

91

сигнала также можно использовать пару комплексно сопряженных колебаний. Однако более удобно использовать одну частоту и его проекцию на действительную ось.

Общий модулированный сигнал можно описать выражением

в котором амплитуда A(t) и мгновенный фазовый угол ω(t) являются функ-

только составляющие с положительными значениями частоты, то речь идет об аналитическом сигнале.

Рассмотрим в качестве примера амплитудно-модулированный сигнал,

в котором частота f0 является фиксированной несущей частотой, а функция A(t) является модулирующей функцией, соответствующей огибающей модулированного сигнала (обычно с определенным смещением постоянного тока). На рис. 4.22 показана составляющая с несущей частотой gc(t) во временной области и ее спектр Gc(f) в частотной области, модулированный сигнал gm(t) с составляющей постоянного тока во временной области и соответствующий спектр Gm(f) в частотной области и модулированный сигнал gc(t) · Gm(t) во временной области и определенный на основе теоремы свертки спектр Gc(f) · Gm(f) последнего. Спектр амплитудно-модулированного сигнала имеет боковые полосы, расположенные на соответствующей частоте модулированного сигнала fm на расстоянии вокруг несущей частоты fc. Отметим, что показанные на рис. 4.22 сигналы являются косинусоидальными волнами, способствующими более наглядному графическому представлению. Однако в общем случае справедливо, что фазовые соотношения обеих боковых полос таковы, что их векторная сумма всегда совпадает с фазором составляющей с несущей частотой. На рис. 4.23 показан аналитический сигнал, соответствующий показанному на рис. 4.22 амплитудномодулированному сигналу.

Этот аналитический сигнал можно рассматривать как один вращающийся фазор, амплитуда которого изменяется по синусоидальному закону между двумя пределами. Путем анализа Фурье можно колебание с изменяющейся амплитудой разложитьнатри колебания сфиксированными амплитудами (см. рис. 4.23).

92

Рис. 4.22. Спектр амплитудно-модулированного сигнала

Рис. 4.23. Амплитуднаямодуляция, представленнаявекторнойсуммойтрехколебаний

93

Процесс разложения более сложен в случае фазовой или частотной модуляции. Однако представление при помощи аналитического сигнала относительно просто даже в этих случаях. Аналитический сигнал, показанный на рис. 4.23, представляет частотно-модулированный сигнал, созданный путем модуляции, имеющей неизменную амплитуду составляющей с несущей частотой модулирующим сигналом с единой частотой.

Математическое выражение, описывающее аналитический сигнал, имеет вид

Символом β обозначено максимальное отклонение фазы (в радианах) от линейно увеличивающегося фазового угла составляющей с несущей частотой f0. Фазовую модуляцию с единой модулирующей частотой можно также рассматривать как частотную модуляцию с единой модулирующей частотой. Мгновенный фазовый угол аналитического сигнала дается выражением

Выражение, определяющее мгновенную частоту, получается путем дифференцирования выражения (4.17), т.е.

Следовательно, максимальное отклонение частоты ∆f равно β, причем β = ∆f/fm называется «коэффициентом модуляции». Рис. 4.22 иллюстрирует как мгновенные фазу и частоту, так и β и ∆f.

Представление модулированного по фазе аналитического сигнала в виде суммы колебаний с фиксированной частотой относительно затруднительно ипредъявляет требования к применению функций Бесселя. На рис. 4.22 показаны примеры (односторонних) спектров амплитуды модулированных сигналов

сразличными значениями коэффициента модуляции β. Можно доказать, что относительные амплитуды составляющей с несущей частотой и боковых полос

n-го порядка равны соответственно J0(β) и Jn(β), причем символом Jn(β) обозначена бесселева функция 1-города синдексом пи аргументом f.

На рис. 4.24 видно, что в случае β < 1 почти вся важная информация сосредоточена в первых двух парах боковых полос, причем при β << 1 достаточна лишь одна пара боковых полос. Эти два случая целесообразно рассмотреть более подробно, так как на их основе можно понять взаимосвязь

самплитудной модуляцией.

Рис. 4.24 иллюстрирует показанный на рис. 4.23 процесс амплитудной модуляции в системе координат, вращающейся с частотой, соответствующей несущей частоте f0 (т.е. умноженной на e j 2πf0t или вычитаемой из частоты f0

94

частот всех составляющих спектра). Результат векторного сложения присущих верхней и нижней боковым полосам несущего сигнала совпадает с частотой модуляции, соответствующей несущей частоте.

Рис. 4.24. Примеры спектров амплитуды, модулированных по частоте сигналов с различными значениями коэффициента модуляции β

В случае, если фаза одной боковой полосы частоты модуляции опрокинута (рис. 4.25), то результатом векторного сложения является модуляция с изменяющейся по синусоидальному закону амплитудой, направленной перпендикулярно к частоте модуляции, составляющей с несущей частотой угол сдвига по фазе. Окончательный результат векторного сложения упомянутых элементов модуляции (гипотенуза) будет колебание с почти неизменной амплитудой, но с фазой, изменяющейся по синусоидальному закону относительно составляющей с несущей частотой. Такая модель фазовой модуляции с одной парой боковых полос приемлема только в случае малых отклонений фазы, т.е. при β << 1.

При увеличении значений β необходимо учесть боковые полосы более высокого порядка с тем, чтобы компенсировать изменения длины упомянутой вышегипотенузы (рис. 4.26). Дляграфического создания результирующей формы

95

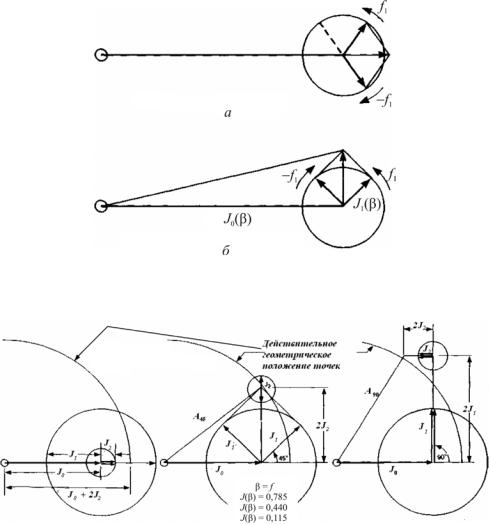
Рис. 4.25. Фазовые соотношения боковых полос при амплитудной (а) и фазовой (б) модуляции

Рис. 4.26. Схема влияния боковых полос второго порядка компенсации изменяющейся длины гипотенузы

колебаний с учетом боковых полос до второго порядка при β = 1 рад использовалисьдействительные значения бесселевых функций J0(β), J1 (β) и J2(β).

В интервале времени, соответствующем одной четвертой оборота боковых полос первого порядка (длина J1(β)), боковые полосы второго порядка (длина J2(β)) поворачиваются на половину оборота. A0° , A45° и A90° представ-

ляют длину результата (с учетом двух пар боковых полос) при равном соответственно 0°, 45° и 90° угловом смещении боковых полос первого порядка. Легко видеть, что длины A0° , A45° и A90° соответствуют длинам сегментов

96

окружности, получаемых на основе всех боковых полос с неизменной амплитудой. Рассмотренный выше пример, вероятно, дает представление о взаимодействии боковых полос при несложной амплитудной или фазовой модуляции в более общих случаях модуляции.

Несмотря на то, что характерным для этих простых видов модуляции является симметричное расположение боковых полос, фазовые соотношения снизу и сверху несущей частоты отличаются друг от друга и обусловливают усиление с одной стороны и ослабление (или даже аннулирование) с противоположной стороны последней. Очевидно, что применение аналитических сигналов при моделировании модулированных по амплитуде или фазе сигналов ограничено и практически допустимо лишь там, где обусловленные модуляцией боковые полосы не перекрывают равную нулю частоту. Модулированный сигнал может быть представлен односторонним или двусторонним спектром также в случае, если обусловленные модуляцией боковые стороны не перекрывают равную нулю частоту (рис. 4.27). Следовательно, в случае амплитудной модуляции несущая частота должна превышать самую высокую модулирующую частоту. В случае частотной модуляции несущая частота должна превышать как 4fm, так и 2∆f (см. рис. 4.18), где fm – самая высокая модулирующая частота и ∆f – максимальное отклонение частоты, соответствующее максимальной амплитуде модулирующего сигнала.

Рис. 4.27. Ограничение ширины боковых полос единой составляющей

снесущей частотой

Вслучае комбинированной амплитудной и частотной (или фазовой) модуляции боковая полоса с самой низкой частотой модулированной по фазе

составляющей ( e jω(1) ) должна превышать самую высокую частоту модулированного по амплитуде сигнала (A(t)).

К более сложным видам колебаний относятся модулированные колебательные процессы

97

у которых один либо несколько параметров изменяются во времени. В зависимости от того, какой из трех параметров периодически изменяется, различают амплитудно-модулированные (АМ), частотно-модулированные (ЧМ) и модулированные по фазе (ФМ) периодические колебания. В большинстве случаев эти параметры изменяются настолько медленно, что в пределах одного периода колебательный процесс можно считать гармоническим.

Во время работы в результате соударения деталей в механизме возбуждаются колебания на собственных частотах. Эти частоты являются константами механизма и не меняются при изменении его состояния. Поэтому само синусоидальное колебание на собственной частоте не несет диагностической информации. Выделение одной из собственных частот ω0, называемой несущей, позволяет оценить структуру колебания на этой частоте. Это колебание можно записать в следующем виде:

т.е. амплитуда и фаза этого гармонического колебания меняются со временем по определенному закону. Изменения амплитуды связаны с тем, что в момент удара в материал механизма передается определенная порция энергии и амплитуда упругих колебаний скачком увеличивается до значения A. Затем энергия колебаний постепенно рассеивается и их амплитуда уменьшается по экспоненциальному закону e−δT . К моменту очередного удара амплитуда колебаний уменьшается до A e−δT , после чего материал снова получает порцию энергии. Изменение амплитуды называют модуляцией, а разность между наибольшим и наименьшим значениями амплитуды, отнесенную к наибольшей амплитуде, называют глубиной модуляции и обозначают

Глубина модуляции зависит от периода следования ударов T и величины коэффициента затухания d. Функция A(t), соответствующая изменению амплитуды синусоидального колебания, называется огибающей сигнала. Ее параметры зависят от интенсивности соударения деталей, частоты следования и фазы импульсов. В момент соударения деталей меняется не только амплитуда, но и фаза колебаний. Согласно высказанным выше соображениям, изменение амплитуды носит пилообразный характер. Но прежде чем рассмотреть этот случай, положим, что амплитуда синусоиды sin(ω0t) меняется также по синусоидальному закону, носозначительно меньшей частотой, чем ω0. Итак,

причем ω0 >>Ω,\R\<1.

98

Раскрывая скобки, получим

Амплитудно-модулированный (АМ) сигнал (рис. 4.28, б) в отличие от весьма похожих по виду биений (рис. 4.28, а) состоит из трех гармонических составляющих, одна из которых имеет частоту несущей ω0, а две другие на-

зывают боковыми: (ω0 – Ω) и (ω0 + Ω).

Рис. 4.28. Биения (а) и амплитудная модуляция (б)

По виду временной реализации виброакустического сигнала часто трудно отличить биения от модуляции при условии, что частота модуляционного сигнала существенно выше (в несколько раз) несущего сигнала, и только спектральный анализ позволяет однозначно оценить характер сигнала. На рис. 4.29 в качестве примера приведен результат записи временного сигнала с экрана прибора при соотношении частоты несущего сигнала к частоте модуляционного ω0 / ωm = 16. Спектральная характеристика данного сигнала (с экрана прибора) приведена на рис. 4.30. Спектр модулированного колебания будет иметь спектральную линию на частоте несущей ω0 и симметрично расположенную по отношению к ней модулирующую частоту ωm.

Рис. 4.29. Временная реализация амплитудно-модулированного сигнала

99

Рис. 4.30. Амплитудно-модулированный вибросигнал

В более сложном случае, когда амплитуда меняется по произвольному закону A(t), эту функцию можно разложить на гармонические составляющие и рассмотреть модуляцию каждой составляющей в отдельности.

Примером частотно-модулированного (ЧМ) колебания является процесс вида

где ∆ω – величина частотного отклонения, называемая девиацией частоты или просто девиацией; Ω – частота гармонической модуляции.

Амплитуда такого процесса не меняется во времени, а частота изменяется по гармоническому закону относительно некоторой несущей частоты ω0. Спектр ЧМ колебания значительно сложнее, чем спектр АМ колебания. При очень малых девиациях (∆ω/Ω<<1) спектр содержит одну центральную и две боковые линии (ω0 – Ω), (ω0 + Ω), имеет ширину 2Ω. При возрастании девиации частот (∆ω/Ω = 0,5...1) приобретает некоторую значимость вторая пара боковых частот, поэтому ширина спектра возрастает до 4Ω.

При увеличении девиации спектр будет включать все новые значимые пары кратных частот. При (∆ω/Ω >>1) ширина спектра ЧМ колебания близка к удвоенной девиации частоты 2Dω, а число линий в спектре будет столь велико, что он может быть ошибочно принят за непрерывный спектр.

Модулированные по фазе колебания тесно связаны с частотно-

модулированными колебаниями, поскольку угловая частота есть не что иное, как скорость изменения фазы колебания ( ω(t) = ϕ(t) / dt ), то фаза колебаний

ϕ(t) = ∫t ω(t)dt + ϕ0 . (4.26)

0

100