Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теплопередача учебное пособие

..pdf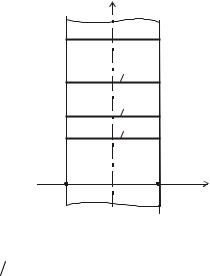

Скачиваний:

Добавлен:

15.11.2022

Размер:

4.77 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

значения числа Bi могут иметь место при малых размерах толщины пластины при больших λ и малых α . При малых Bi температура на поверхности пластины незначительно отличается от температуры на оси. Это указывает на то, что температура по толщине распределяется равномерно и кривая температур остается практически параллельной оси 0x для любого момента времени (рис. 1.20). На

рис. 1.19 и 1.20 Fo1 < Fo2		< Fo3 ... .
Когда число	Bi	находится
в пределах 0,1≤ Bi≤	100,	X0 =1 Bi

есть некоторая конечная величина

(см. рис. 1.18).

	Θ
Θ= 1	Fo= 0
	Fo1
	Fo2
	Fo3
−1	1	X
	0

Рис. 1.20. Распределение температуры в плоской стенке при ее охлаждении в условиях Bi → 0

1.5.2. Охлаждение (нагревание) бесконечного цилиндра

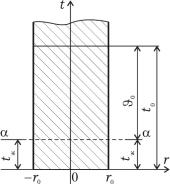
Цилиндр, радиус которого r0 намного меньше его длины, в начальный момент времени имеет по сечению одинаковую температуру t(x, 0) = t0 (рис. 1.21) [1]. Охлаждение цилиндра

происходит через его боковую поверхность при условии, что коэффициент теплоотдачи α во всех точках боковой поверхности одинаков и остается постоянным на протяжении всего периода охлаждения. Температура окружающей среды tж и тепло-

физические свойства цилиндра постоянны. При заданных условиях температурное поле внутри цилиндра будет симметричным относительно оси цилиндра и будет зависеть от текущего радиуса r и времени τ . Как и в подразд. 1.5.1, введем переменную

ϑ = t − tж .

При этих условиях дифференциальное уравнение теплопроводности в цилиндрической системе координат запишем в виде

∂ ϑ	∂	ϑ2			1∂ϑ
	= a			+			.	(1.157)
∂ τ		r	2		r∂
	∂					r

Для переменной ϑ начальные условия примут вид

ϑ (r,0) = t(r,0) −tж = t0 −tж =ϑ 0. (1.158)

Рис. 1.21. Охлаждение бесконечного цилиндра Так как температурное поле

осесимметрично, то граничное условие на оси цилиндра имеет вид

∂ ϑ	= 0 при τ > 0.
		(1.159)

∂ r r =0

Граничное условие на поверхности цилиндра запишем

∂ ϑ	= −	α	ϑ		при τ > 0.
				r =r0		(1.160)

∂ r r =r0		λ

Для решения поставленной задачи используем метод разделения переменных:

ϑ (r, τ) = φ(τ)ψ(r ).

(1.161)

После подстановки выражения (1.161) в уравнение (1.157) запишем

∂ φ(τ)

∂

ψ(

)

1∂

ψ(

)

ψ(r )

= φ(τ)a

(1.162)

∂ τ

∂

∂ r

В результате преобразования уравнения (1.162) получим два обыкновенных дифференциальных уравнения:

φ′(τ) + ak 2φ(τ) = 0;			(1.163)
ψ′′(r) +	1	ψ′(r) + k 2 ψ(r) = 0.	(1.164)

	r
Решениями уравнений (1.163) и (1.164) являются, соответ-
ственно, выражения:
φ(τ) = C1 e−ak 2 τ ;			(1.165)
ψ(r ) = C2 J0 (kr ) + C3Y0 (kr ),			(1.166)
где C1 , C2 , C3 – постоянные интегрирования; J0 и Y0			– функции

Бесселя первого и второго рода нулевого порядка.

После подстановки выражений (1.165) и (1.166) в уравнение (1.161) получим

ϑ (r, τ) = C1 e−ak 2 τ C2 J0 (kr )						+ C3Y0 (kr ) .			(1.167)

Так как температура при		r = 0			имеет конечное значение,
а Y0 (0) → ∞ , то из физических соображений уравнение (1.167)
не должно содержать функцию Y0 (kr ),						поэтому C3			должно быть
равнонулю. Таким образом, уравнение(1.167) принимает вид
	ϑ (r, τ) = Ae−ak 2 τ J0 (kr ) ,								(1.168)
здесь A = C1C2 .
Обозначим kr0	= µ , тогдауравнение(1.168) будетиметь вид
	−µ		2 aτ				r
	−µ		2
ϑ	(r, τ) = Ae			r0 J0		µ		.	(1.169)
ϑ	(r, τ) = Ae			r0 J0		µ		.	(1.169)
							r0
									73

Используя граничное условие (1.160) и выражение (1.169) при r = r0 , получим

−µ

2 aτ

−µ

2 aτ

−

= −

(1.170)

здесь J1 – функции Бесселя первого рода первого порядка.

После преобразования уравнения (1.170) получим следующее характеристическое уравнение:

J0 (µ)	=	µ	=	µ	,	(1.171)
		αr0
J1 (µ)				Bi
		λ

где Bi – число Био, Bi = αλr0 .

Характеристическое уравнение (1.171) имеет бесконечное множество решений µ1 , µ2 , …, µn , …

Общим решением дифференциального уравнения теплопроводности (1.157) является сумма частных решений (1.169):


∞	µi	r	ехр −µi2	aτ	.
ϑ = ∑ Ai J0						(1.172)
				2
i =1		r0		r0

Постоянные интегрирования Ai определяются исходя из

распределения температуры в нулевой момент времени ( τ = 0 ). Если в начальный момент времени температура постоянна ( t(x, 0) = t0 ), то уравнение (1.172) запишется в виде

	∞							ϑ 0 2J1 (µi )																r		2 aτ
ϑ = ∑								ϑ 0 2J1 (µi )																r		2 aτ
																					J	0	µi		exp	−µi			, (1.173)
			µ		J			2	(µ			)	+ J			2	(µ		)		J	0	µi	r	exp	−µi	r	2	, (1.173)
i =1			µ		J			0	(µ			)	+ J			1	(µ		)					r			r
				i				0			i					1		i						0			0
∞						ϑ 0 2J1 (µi )
здесь Ai = ∑						ϑ 0 2J1 (µi )														.
здесь Ai = ∑			J			2	(			)	+		J	2	(			)		.
i 1			J			0	(			)			J	1	(			)
=		µi				0		µi						1		µi

Уравнение (1.173) в безразмерном виде примет вид

∑

2J1 (µi )

0 (

)

(

)

Θ =

∞

exp−

µ2 Fo

(1.174)

µi

)

(

µi

i 1

(

)

где Θ – безразмерная температура, Θ =

ϑ ϑ

0 ; R – безразмерная

координата,

которая изменяется в пределах 0 ≤

R≤

R = r r0 ;

Fo – безразмерное время (числоФурье) дляцилиндра, Fo = aτr02 .

Необходимо отметить, что выводы, сделанные при анализе решения для пластины, справедливы и для цилиндра.

Регулярный режим охлаждения или нагревания тел.

Рассмотрим процесс охлаждения (или нагревания) твердого тела, когда условия охлаждения, температура окружающей среды tж и коэффициент теплоотдачи α , во времени остаются постоянными и внутренние источники теплоты в теле отсутствуют.

Анализ полученных аналитических решений нестационарных задач теплопроводности для тел различной геометрии показывает, что они имеют одинаковую структуру, т.е. представляют собой сумму бесконечного ряда, члены которого расположены по быстро убывающим экспоненциальным функциям [1, 2]. Например, для неограниченной пластины

∞	cos µi	x	ехр −µi2		аτ	,
ϑ = ∑ Аi		x			аτ				(1.175)
ϑ = ∑ Аi		δ			2				(1.175)
i =1		δ			δ
здесь Аi – постоянные коэффициенты,				определяемые началь-
ным распределением температуры; множитель cos							µi	x	зави-
ным распределением температуры; множитель cos							µi	δ	зави-
								δ
сит только от координаты x и его можно обозначить Ui									; экспо-

τ µ2 а

нента убывает при увеличении времени ; выражение i обо-

δ2

значим через mi , причем m1 < m2 < m3 < ... < mi ...

Таким образом, выражение (1.175) можно записать в виде

∞
ϑ = ∑ АiUi е−mi τ.	(1.176)

i =1

Уравнение (1.176) будет справедливо и для тел других геометрических форм. Отличие будет состоять в том, что величины Аi и Ui будут определяться другими выражениями. Мно-

житель Аi зависит также от распределения температуры в нуле-

вой момент времени.

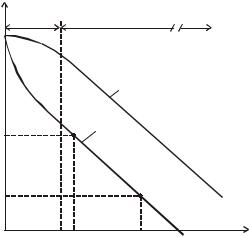
Нестационарный процесс охлаждения тела может быть разделен на три стадии: начальная стадия (I стадия на рис. 1.22),

стадия регулярного режима (II стадия на рис. 1.22), третья стадия охлаждения соответствует стационарному режиму, когда температура во всех точках тела равна температуре окружающей среды (тепловое равновесие).

ln ϑ	I стадия		II стадия
			x = 0
ln ϑ		0 < x ≤ δ
ln ϑ	1
ln ϑ	2
		τ Р τ 1	τ 2	τ
	0	τ Р τ 1	τ 2
	Рис. 1.22. Зависимость ln ϑ			от времени
	при охлаждении (нагревании) тел

В интервале времени от τ = 0 до τ = τр (начальная стадия

охлаждения) перераспределение температурного поля во многом зависит от начального распределения температуры в теле, поэтому характер процесса охлаждения на данном этапе не определяется однозначно условиями охлаждения и свойствами тела. Время τ = τр соответствует безразмерному времени Fo = 0,3 . В этих ус-

ловиях температурное поле в теле будет определяться не только первым, но ипоследующими членами ряда уравнения (1.176).

С увеличением	времени τ , с учетом соотношения
m1 < m2 < m3 < ... < mi ... ,	последующие члены ряда уравнения

(1.176) по отношению к первому члену будут быстро убывать, т.е. ряд становится быстро сходящим. С момента времени τ > τр

( Fo > 0,3 ) ряд становится настолько быстро сходящимся, что распределение температуры достаточно точно описывается первым членом ряда:

ϑ = А1U1е−m1τ .

(1.177)

На этом этапе охлаждения начальные условия начинают играть второстепенную роль, и процесс полностью определяется только условиями охлаждения на границе тела и среды, физическими свойствами тела и его геометрической формы и размерами. Это соотношение показывает, что изменение избыточной температуры как в пространстве, так и во времени не зависит от начального распределения температуры.

Логарифмируя уравнение (1.177) и опуская индексы, получаем

lnϑ = −mτ+ C ,

(1.178)

где C = ln ( АU ).

Из этого уравнения следует, что величина lnϑ для каждой точки тела изменяется во времени по линейному закону

(см. рис. 1.22). Эта стадия охлаждения называется регулярным режимом охлаждения.

При длительном охлаждении ( τ → ∞ ) всеточкитела в конце концов принимают одинаковую температуру, равную температуре окружающей среды tж (стационарныйрежим).

Продифференцируем выражение (1.178) по τ :

1 ∂ ϑ	= −m = const.	(1.179)

ϑ ∂ τ

Величина m (с–1) есть положительное число, не зависящее от координат и времени. Эта величина характеризует интенсивность охлаждения (нагревания) тела и называется темпом охлаждения (нагревания). Темп охлаждения характеризует относительную скорость изменения температуры в теле и зависит от физических свойств тела, процесса охлаждения на его поверхности, геометрической формы и размеров тела.

Величину темпа охлаждения можно определить по результатам эксперимента (см. рис. 1.22):

lnϑ 1 − lnϑ 2	= m = const.	(1.180)

τ2 − τ1

Выражение для темпа охлаждения m можно найти также из анализа теплового баланса. Убывание внутренней энергии тела определяется из уравнения


dQ = −cρV	∂ ϑ V	dτ,	(1.181)

	∂ τ

где c – удельная теплоемкость; ρ – плотностьвещества; V – объем тела; ϑ V – средняяпообъемуизбыточнаятемпература; τ – время.

Убывание внутренней энергии происходит за счет отвода тепла с поверхности тела в окружающую среду за счет процессов теплоотдачи:


dQ = αϑ F F dτ,			(1.182)

где α – среднее значение коэффициента теплоотдачи; F – площадь поверхности тела; ϑ F – средняя температура по поверхности тела в данный момент времени:

∫

F =

ϑ F dF.

(1.183)

Приравнивая правые части выражений (1.182) и (1.183)

при равенстве левых, получаем

−

∂ ϑ V

αF

ϑ F .

(1.184)

∂ τ

cρV

После деления левой и правой частей выражения (1.184)

на ϑ V , запишем

−

∂ ϑ V

αF

F .

(1.185)

ϑ V

∂ τ

cρVϑ V

С учетом уравнений (1.179) и (1.185) темп охлаждения

можно определить по формуле

m = ψ

αF

(1.186)

cρV


где ψ – коэффициент неравномерности распределения темпера-

туры в теле, ψ = ϑ		F .
туры в теле, ψ = ϑ
	ϑ V
При Bi →	0 температура в теле распределяется равномер-

но, поэтому ϑ F	=ϑ V , ψ =1 , при Bi → ∞		ϑ F = 0 и ψ = 0 . Таким

образом, коэффициент неравномерности распределения температуры ψ лежит в диапазоне от 0 до 1.

При коэффициенте теплоотдачи α → ∞ ( Bi → ∞ ) темп охлаждения m∞ прямо пропорционален температуропроводности тела:

a = Km∞ ,

(1.187)

где K – коэффициент формы, зависящий от формы и размеров тела, м2.

Например, для бесконечной пластины толщиной 2δ при

Bi → ∞ ( µ = π 2 ) и Fo=

aτ

>> 0,3

= e

∞

, откуда

–µ2 Fo

-m

δ2

m∞ =

µ12 a

π2 a

4δ

2δ

Поэтому для плоской бесконечной пластины толщиной 2δ коэффициент формы K определяется из выражения

K = 1 .

(π2δ)2

Коэффициенты формы для тел других геометрических форм следующие:

♦для параллелепипеда со сторонами l1 , l2 , l3

K =

;

(1.188)

♦для цилиндра радиусом R и длиной l

K =		1			;	(1.189)
	2, 405	2		π 2
			+
	R
				l

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20227.59 Mб12Теория технологических процессов учебное пособие..pdf
#
15.11.202219.88 Mб46Теория управления..pdf
#
15.11.20223.96 Mб28Теория электропривода учебное пособие..pdf
#
15.11.2022548.89 Кб3Теория электропривода..pdf
#
15.11.2022548.89 Кб3Теория электропривода.pdf
#
15.11.20224.77 Mб38Теплопередача учебное пособие..pdf
#
15.11.202210.8 Mб12Теплофизика в металлургии..pdf
#
15.11.20227.09 Mб13Теплофизические явления в полимерных материалах при интенсивном и кр..pdf
#
15.11.20221.69 Mб11Тестовый контроль по математике учебно-методическое пособие..pdf
#
15.11.202210.87 Mб21Техника технология и технические средства применяемые при реконстру..pdf
#
15.11.20221.1 Mб11Техника высоких напряжений..pdf