Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теплопередача учебное пособие

..pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

4.77 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Первое интегрирование даст
	∂ t	= С1 .	(1.23)

	∂ x
После второго интегрирования получим
t = C1 x + C2 .			(1.24)

Таким образом, температура изменяется по линейному закону.

Используя граничные условия, найдем постоянные интегрирования:

при x = 0	t = t1		и C2		= t1;
при x = δ	t = t2		и C1		= −	t1 − t2	.

В результате получаем						δ

t = t1	−	t1 − t2		x .	(1.25)

		δ

Для определения количества тепла, проходящего через единицу поверхности стенки в единицу времени в направлении


оси 0x , воспользуемся			законом					Фурье,		согласно которому
q = −λ	dt	. Учитывая, что		dt		= C1		= −	t1 − t2	, после подстановки
									δ
	dx			dx
значения dt dx в выражение закона Фурье получим
		q =			λ		(t1 − t2 ) .			(1.26)

					δ

Отношение λ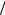δ [Вт/(м2·°С)] называется тепловой проводимостью стенки, а обратная величина δ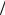λ [(м2·°С)/Вт] – тепловым или термическим сопротивлением стенки.

Зная плотность теплового потока, легко вычислить общее количество теплоты Q, которое передается через поверхность стенки величиной F за промежуток времени τ :

Q = qFτ =	λ	(t1 − t2 ) Fτ .	(1.27)
	δ

1.4.2. Передача теплоты через плоскую стенку

( qV = 0 , λ = f (t ) )

Рассмотрим задачу передачи теплоты через плоскую стенку для случая, когда зависимость коэффициента теплопроводности λ от температуры t определяется линейным уравнением [1, 2]:

λ = λ0 (1 + bt ),

где λ0 – величина коэффициента теплопроводности при t = 0 °С.

По закону Фурье
q = −λ(t)			dt	= −λ0			(1+ bt)		dt	.	(а)

			dx						dx
После преобразования					уравнения (а) и интегрирования
в пределах от x = 0 до x = δ и от t1							до t2	получим
qδ = λ0					(t1 + t2 )			− t2 ) .			(б)
	1 + b				2		(t1

Множитель λ0 1 + b		t1 + t2				в уравнении (б) представляет

	2

собой среднеинтегральное значение коэффициента теплопроводности. В этом можно убедиться, вычислив интеграл

		1	t1				t1 + t2
λср =			∫ λ(t)dt =λ0			+ b
	t1				1		2	.	(1.28)
		− t2 t		2

Таким образом, плотность теплового потока q пластины

определяется по формуле
q =	λср	(t1 − t2 ) .	(1.29)

	δ

Для того чтобы найти распределение температуры в стенке, необходимо проинтегрировать выражение (а) в пределах от

x = 0 до любой текущей координаты x

и в интервале темпера-

тур от t1 до t :

q∫ dx = −λ0 ∫ (1+ bt)dt ;

qx = −λ0 (t1 − t2 ) +

(t 2 − t12 ) ;

t 2 + t −

t12 − t1 +

= 0 │×

;

λ0

1 2

2qx

t +

−

t1 −

= −

;

bλ0

2qx

t +

−

= −

;

bλ0

2qx

t =

t1 +

−

(1.30)

bλ0

Из уравнения (1.30) видно, что температура по толщине стенки имеет нелинейный характер зависимости.

1.4.3. Передача теплоты через многослойную стенку, состоящую из n однородных слоев

Допустим, что между слоями имеет место идеальный контакт и температура соприкасающихся слоев одинакова [1, 2].

Для стационарного режима теплопроводности плоской бесконечной стенки, в том числе и многослойной, плотность теплового потока есть величина постоянная и для всех слоев одинакова

q = const .

При заданных коэффициентах теплопроводности и толщинах каждого слоя и граничных условиях первого рода на левой и правой границах получим систему из n уравнений:

q =	λ1	(t1		− t2 );

	δ1
	δ1
q =	λ2	(t2 − t3 );
q =		(t2 − t3 );					(а)
	δ2						(а)


q =	λn	(t		− t	n+1	).
q =		(t	n	− t		).
	δn		n
	δn

Выполнив преобразования и сложив этиуравнения, получим

		δ1		δ2	+ +	δn
t1 − tn+1	= q		+				.
		λ1		λ2
						λn

Выразив плотность теплового потока, запишем

q =

t1 − tn+1

(1.31)

δ1

δn

δ2

δi

+ +

∑i 1

δi

здесь ∑

– полное термическое сопротивление теплопровод-

i 1

ности многослойной стенки.

Иногда удобно представить многослойную стенку как

однородную толщиной ∑δi . При этом в расчет вводится так

i=1

называемый эквивалентный коэффициент теплопроводности, который определяется так:

	n
λэкв =	∑δi
	i =1		.	(1.32)
	n
	∑	δi
		λi
	i =1

Определив q по формуле (1.31) и воспользовавшись сис-

темой уравнений (а), можно вычислить температуры на границах соприкосновения двух соседних слоев:

= t

− q

δ1

;

λ1

δ1

δ2

= t1

− q

;

λ1

(1.33)

λ2

t j 1 = t1 − q

δi

∑i =1

λi

здесь индекс j может принимать значения 1, 2, ..., n.

1.4.4. Теплопроводность через плоскую стенку. Граничное условие третьего рода

Теплопередачей называется перенос тепла от одной подвижной среды (жидкости или газа) к другой через разделяющую их твердую стенку [1].

Теплопередача включает в себя теплоотдачу от более горячей подвижной среды к стенке, теплопроводность стенки, теплоотдачу от другой стенки к более холодной подвижной среде.


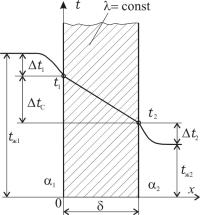
		На рис. 1.6 представлен
	процесс		теплоотдачи		через
	однородную			плоскую	стенку
	толщиной δ , с коэффициентом
	теплопроводности λ.
		В данной задаче на по-
	верхностях			твердой	стенки
	заданы		граничные условия
	третьего рода, при которых
	процесс		теплообмена		между
	стенками и окружающей среды
	определяется			законом	Нью-
Рис. 1.6. Теплопередача через	тона–Рихмана (1.16). Подвиж-
	ная	окружающая среда слева
плоскую стенку	от	стенки		характеризуется

температурой tж1 и коэффициентом теплоотдачи α1 , а справа соответственно – tж2 и α2 . Будем

считать, что эти параметры не изменяются во времени и по поверхности. Это позволяет решать задачу в одномерной постановке, учитывая изменение температуры только по координате х.

В результате решения задачи теплообмена между подвижными средами через плоскую стенку определим плотность теплового потока и температуры на поверхности стенки.

По закону Ньютона–Рихмана плотность теплового потока

на левой границе
q = α1 (tж1 − t1 ).			(1.34)
Плотность теплового потока в стенке определяем по вы-
ражению (1.26):
q =	λ	(t1 − t2 ).	(1.35)

	δ

На правой границе та же плотность теплового потока находим по формуле

q = α2 (t2 − tж2 ).

(1.36)

Тогда, после преобразования уравнений (1.34)–(1.36), запишем систему уравнений

	1
q			= tж1 − t1;
q	α1		= tж1 − t1;
	α1
	δ
q		= t1 − t2 ;			(1.37)
q	λ	= t1 − t2 ;			(1.37)
	λ
	1		= t2 − tж2
q				.
q	α2			.
	α2

После сложения уравнений (1.37) получим

	1		δ		1
q		+		+		= tж1	− tж2 .	(1.38)
	α1		λ		α2

После преобразования уравнения (1.38) находим плотность теплового потока:

q =	tж1 − tж2
						.				(1.39)
	1	+	δ	+	1	.				(1.39)
	α1		λ α2
Уравнение (1.39) можно переписать в виде
q = k (tж1 − tж2 ) ,										(1.40)
здесь k – коэффициенттеплопередачи, Вт/(м2·°С), k =									1			.

							1	+	δ	+	1
							α1		λ		α2

Коэффициент теплопередачи k характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую стенку и численно равен количеству теплоты, которое

передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в 1 °С.

Полное термическое сопротивление теплопередачи есть величина, обратная коэффициенту теплопередачи:

R =	1	=	1	+	δ	+	1	.	(1.41)

	k		α1		λ		α2

Термическое сопротивление теплопередачи плоской однослойной стенки R складывается из частных термических сопротивлений 1α1 , δλ и 1α2 .

Для многослойной стенки

R = 1 =

1 + ∑ δi

+ 1 ,

i 1

k =

δi

+ ∑

i 1

Тогда плотность теплового потока

q =		tж1 − tж2						.	(1.42)
		n	δi
1		+ ∑			+	1
	α					α
		i 1	λ	i			2
1		=

Тепловой поток Р, Вт, через поверхность стенки площадью F определяется по формуле

P = q F = k ∆ t F .

(1.43)

Температуры левой и правой поверхностей плоской стенки можно найти из системы уравнений (1.37):

	1						δ		1
t1 = tж1 − q		;	t2	= tж1 − q				+		,
t1 = tж1 − q		;	t2	= tж1 − q			λ	+	α1	,
	α1						λ		α1
или
	t2 = tж2 + q				1	.

					α2

Сравнивая между собой формулы (1.31) и (1.42), можно сделать вывод, что граничное условие первого рода является частным случаем граничного условия третьего рода. Если в уравнении (1.42) коэффициенты теплоотдачи стремятся к бесконечности, то данное уравнение преобразуется в уравнение (1.31).

Температура на границе слоев многослойной стенки при теплопередаче может быть определена по формуле

			1	j	δi
t j +1	= tж1	− q		+ ∑		,	(1.44)
			α1
				i =1	λi

где j = 1, 2,..., n.

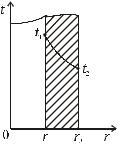
1.4.5. Передача теплоты через цилиндрическую стенку (qV = 0)

Рассмотрим стационарную задачу теплопроводности в трубе (цилиндрической стенке) [1, 2], схема которой представлена на рис. 1.7.

На внутренней поверхности диаметром d1 = 2r1 и внешней поверхности диаметром d2 = 2r2 заданы граничные условия первого рода с темпера-

Рис. 1.7. Теплопроводность цилиндрической стенки

турами соответственно t1 и t2 . Задан постоянный коэффициент

теплопроводности λ.

Для решения задачи стационарной теплопроводности необходимо найти распределение температуры по радиусу цилиндрической стенки и тепловой поток через нее.

Дифференциальное уравнение теплопроводности в цилиндрической системе координат для этой задачи будет иметь вид

∂ 2t

1∂ t

1 ∂

∂

0 .

(1.45)

r∂

∂

∂ r2

r r 2∂

φ2

Ось 0z совмещена с осью цилиндрической стенки.

В данной постановке температура изменяется только радиусу, поэтому

	∂ t	= 0 ;		∂ 2t	= 0 ;
	∂ z	= 0 ;		∂ z2	= 0 ;
	∂ z			∂ z2
	∂ t		= 0 ;	∂ 2t		= 0 .
∂ φ			= 0 ;	∂ φ2		= 0 .
∂ φ				∂ φ2

по

(а)

(б)

C учетом (а) и (б) уравнение теплопроводности (1.45) будет иметь вид

	d 2t		+	1	dt		= 0 .			(1.46)
	dr 2		+				= 0 .			(1.46)
	dr 2			r dr
Граничные условия:
при		r = r1				t = t1 ;
при		r = r					t = t	2	.	(1.47)
		2						2

Для решения уравнения (1.46) введем переменную u:

u =	dt	,	(в)

	dr

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20227.59 Mб12Теория технологических процессов учебное пособие..pdf
#
15.11.202219.88 Mб46Теория управления..pdf
#
15.11.20223.96 Mб28Теория электропривода учебное пособие..pdf
#
15.11.2022548.89 Кб3Теория электропривода..pdf
#
15.11.2022548.89 Кб3Теория электропривода.pdf
#
15.11.20224.77 Mб38Теплопередача учебное пособие..pdf
#
15.11.202210.8 Mб12Теплофизика в металлургии..pdf
#
15.11.20227.09 Mб13Теплофизические явления в полимерных материалах при интенсивном и кр..pdf
#
15.11.20221.69 Mб11Тестовый контроль по математике учебно-методическое пособие..pdf
#
15.11.202210.87 Mб21Техника технология и технические средства применяемые при реконстру..pdf
#
15.11.20221.1 Mб11Техника высоких напряжений..pdf