Теплопередача учебное пособие

Для количественного описания конвективного теплообмена нужно составить замкнутую систему дифференциальных уравнений. Для их получения сделаем следующие допущения:

1.Подвижная среда является сплошной.

2.В потоке жидкости выполняются законы сохранения энергии, массы и количества движения.

3.Процесс теплообмена между потоком жидкости и поверхностью твердого тела определяется законом Ньютона– Рихмана (2.4).

4.Физические свойства жидкости (коэффициент тепло-

проводности λ , удельная теплоемкость c, плотность ρ , динамическая вязкость µ) считаются заданными функциями состояния жидкости.

2.2. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ КОНВЕКТИВНОГО ТЕПЛООБМЕНА

2.2.1. Уравнение энергии

Выделим в потоке жидкости неподвижный относительно координатной системы элементарный параллелепипед (см. рис. 1.3) [1, 2]. Будем считать, что через грани параллелепипеда происходит перенос тепла, как за счет теплопроводности, так и за счет конвекции. Имеется внутренний источник тепла, который распределен равномерноповсемуэлементарномуобъему.

Ранее было получено уравнение энергии для твердого тела (1.7)

ρс∂∂ τt = −div q + qV ,

или в декартовой системе координат

Данное уравнение справедливо и при конвективном переносе тепла.

Согласно уравнению (2.3) проекции плотности теплового потока определяются по формулам:

Уравнение (2.13) называется уравнением энергии при конвективном теплообмене. В уравнение (2.13) подставляются теплофизические параметры жидкости. В общем случае компоненты вектора скорости v в уравнении (2.13) являются искомыми величинами. Чтобы сделать систему уравнений замкнутой, необходимо добавить уравнения, которые бы описывали изменение скорости во времени и пространстве. Такими уравнениями являются дифференциальные уравнения движения.

92

2.2.2. Уравнения движения

Рассмотрим упрощенный способ вывода дифференциального уравнения движения для случая одномерного движения несжимаемой жидкости [1, 2], вывод которого основан на втором законе Ньютона. Этот вывод не является строгим, его основное достоинство заключается в наглядности. Дифференциальные уравнения движениядлятрехмерногослучаябудутприведеныбезвывода.

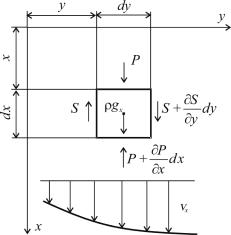
Выделим в потоке вязкой жидкости элементарный объем в форме параллелепипеда со сторонами dx , dy , dz (рис. 2.1).

Движение жидкости направлено по координате x, по двум другим координатам компоненты скорости равны нулю. Изменение компоненты скорости vx происходит только по координате y.

На элемент жидкости действуют сила тяжести, равнодействующая сил давления и равнодействующая сил трения. Сила тяжести действует на каждую частицу в рассматриваемом объеме, а силы вязкого трения и давления приложены к поверхностям.

Рис. 2.1. К выводу дифференциального уравнения движения жидкости

93

Сила тяжести приложена в центре тяжести элемента объ-

здесь gx – проекция ускорения свободного падения; ρ – плот-

ность подвижной среды.

Равнодействующая сил давления определяется на основе следующих соображений. На верхнюю грань действует сила давления P dy dz . К нижней грани приложена противодейст-

ние этой силы противоположно оси 0x , то в данном выражении присутствует знак минус. Тогда

дит только в направлении оси 0 y , то на боковых гранях элемен-

та жидкости возникает сила трения. Около левой грани скорость движения частиц меньше, чем в самом элементе, поэтому здесь в сечении y сила трения направлена против движения и равна S dx dz . Около правой грани, наоборот, скорость движения час-

тиц жидкости больше, чем в самом элементе, поэтому здесь

рону движения. Равнодействующая этих сил равна алгебраической сумме:

94

В рассматриваемой одномерной постановке напряжение сдвига определяется по формуле

Суммируя df1 , df2 , df3 , получаем проекцию на ось 0x равнодействующей всехсил, приложенныхк объему:

Согласно второму закону Ньютона эта равнодействующая равна произведению массы элемента на его ускорение:

Приравнивая правые части уравнений (2.19) и (2.20) и производя сокращение, окончательно имеем уравнение движения вдоль оси 0x :

В трехмерной постановке уравнения движения с постоянными физическими параметрами имеют следующий вид:

95

В направлении оси 0x в параллелепипед втекает масса жидкости

Величина ρvx представляет собой количество массы, про-

текающее в единицу времени через единицу поперечного сечения. Из противоположной грани вытекает масса

масса, вытекающая из элементарного параллелепипеда в направлении оси 0x,

массы жидкости, вытекающей из объема в направлении оси 0x :

избыток массы жидкости, вытекающей из рассматриваемого элементарного объема в направлении всех трех осей. Этот избыток обусловливается изменением плотности жидкости в объеме dV и равен изменению массы данного объема во вре-

мени ∂∂ ρτ dVdτ. Произведя сокращение на dV и dτ и перенеся

все члены в левую часть равенства, окончательно получим дифференциальное уравнение сплошности или неразрывности для сжимаемых жидкостей:

98

Для несжимаемых жидкостей, полагая ρ = const ,

Уравнение сплошности является уравнением сохранения массы.

2.2.4. Условия однозначности

Полученные дифференциальные уравнения конвективного теплообмена описывают бесконечное множество конкретных процессов. Чтобы выделить рассматриваемый процесс и определить его однозначно, к системе дифференциальных уравнений нужно присоединить условия однозначности [1–5].

Условия однозначности дают математическое описание всех частных особенностей рассматриваемого явления и включают в себя:

1)геометрические условия, характеризующие форму и размерытелаилисистемы, в которой протекает процесс;

2)физические условия, характеризующие физические свойства среды; временные или начальные условия, характеризующие особенности процесса в начальный момент времени (в стационарных задачах не используют эти условия);

3)граничные условия, характеризующие особенности протекания процесса на границах жидкой среды.

Система дифференциальных уравнений в совокупности

сусловиями однозначности представляет собой математическую формулировку краевой задачи.

2.3. ГИДРОСТАТИЧЕСКИЙ И ТЕПЛОВОЙ ПОГРАНИЧНЫЕ СЛОИ

Для инженерной практики особый интерес представляет теплообмен между жидкостью и омываемым ею телом.

99

Рассмотрим особенности течения и переноса теплоты в пристенном слоежидкости [1, 2].

Условие прилипания. В настоящее время в гидродинамике вязкой жидкости получила распространение гипотеза о том, что частицы жидкости, непосредственно прилегающие к твердому телу, прилипают к его поверхности, т.е. их скорость равна скорости тела (а если тело неподвижно, то – нулю). Этот слой прилипшей жидкости нужно рассматривать как бесконечно тонкий слой.

Уравнение теплоотдачи. Поскольку у поверхности твердого тела имеется бесконечно тонкий слой неподвижной жидкости, то плотность теплового потока на стенке со стороны жидкости может быть определена из уравнения Фурье:

где n – нормаль к поверхности; λ – теплопроводность жидкости. С другой стороны, плотность теплового потока с поверхности тела в окружающую подвижную среду определяется уравнением Ньютона–Рихмана (2.4). Тогда при условии равенства левых частей уравнений (2.4) и (2.29) и известном распределении температуры в приграничной области можно опреде-

лить коэффициент теплоотдачи:

Уравнение (2.30) носит название уравнения теплоотдачи.

Гидродинамический пограничный слой. Рассмотрим про-

дольное обтекание плоской поверхности твердого тела безграничным потоком жидкости (рис. 2.3). Скорость и температура невозмущенного потокапостоянныиравны соответственно v0 и t0 .

При прохождении потока жидкости вблизи поверхности пластины в результате действия сил вязкого трения образуется

100