Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теплопередача учебное пособие

..pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

4.77 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

основан на допущении возможности замены непрерывного процесса скачкообразным как во времени, так и в пространстве.

При решении многих практических задач по охлаждению

инагреванию тел начальным режимом процесса пренебрегают, т.е. пренебрегают режимом, характеризующим начальную стадию процесса. Тогда остается только второй режим, в котором относительная скорость изменения температуры во всех точках тела одинаковая. Этот режим подчиняется простому экспоненциальному закону

иназывается регулярным. Существует ряд способов использования теориирегулярногорежимадлярешенияпрактическихзадач.

1.5.1. Аналитическое описание процесса

Для получения аналитического решения необходимо записать дифференциальное уравнение теплопроводности решаемой задачи с учетом допущений и условий однозначности.

Дифференциальное уравнение нестационарной теплопроводности при qV = 0 в декартовой системе координат имеет вид

∂ t

∂ 2t ∂

2t ∂

= a

(1.122)

∂ τ

∂ x

∂

Уравнение (1.122) дополним условиями однозначности:

1)теплофизическими параметрами материала объекта: λ, c,

иρ ( а = λ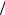сρ );

2)геометрическими размерами и формой исследуемого объекта: l0 , l1 ,…, ln ;

3)температурой объекта в нулевой (начальный) момент времени τ = 0 t = t0 = f (x, y, z) ;

4)граничными условиями.

В результате решения поставленной задачи необходимо найти распределение температуры:

t = f (x, y, z, τ, α, t0 , tж , l0 , l1 , ... , ln ) .	(1.123)
	61

Рис. 1.16. Охлаждение неограниченной пластины

Охлаждение (нагревание) неограниченной пласти-

ны. Рассмотрим плоскую пластину толщиной 2δ (рис. 1.16). Заданы теплофизические параметры пластины: λ, c, и ρ. Бу-

дем считать, что пластина неограниченная, т.е. длина и ширина пластины много больше ее толщины.

С левой и правой стороны заданы одинаковые граничные условия третьего рода. При этом температура окружающей среды tж и коэффици-

енты теплоотдачи α являются постоянными величинами. Градиенты температур понаправлениям y и z равнынулю, аизменение

температуры происходит только по координате x ( ∂ t ∂ x≠ 0 ). Температура в нулевой момент времени в каждой точке пластины постоянна: t(x, 0) = t0 . При этомбудем считать, что t0 > tж .

Для решения задачи сместим начало координат относительно температуры t на величину температуры окружающей среды tж и введем новую переменную ϑ , которая определяется

выражением ϑ = t− tж .

Тогда дифференциальное уравнение нестационарной теплопроводности в одномерной постановке относительно переменной ϑ примет вид

	∂ϑ		∂	ϑ 2
	∂τ	=	а∂		.	(1.124)
				x2
Для переменной ϑ	начальное условие имеет вид
ϑ (x, 0)=	t(x, 0)−		tж= t0− tж= ϑ 0 .			(1.125)

В связи с тем, что задача симметрична относительно оси симметрии, совместим начало координат по x с осью пластины

(см. рис. 1.16).

При этом

ϑ (x)= ϑ −( x) при 0 ≤ x≤ δ τ ,> 0 .

(1.126)

Из симметрии температуры следует, что

∂ϑ			= 0 при τ > 0 .
				(1.127)
	∂
		х	х=0

Таким образом, достаточно определить температуру для одной половины пластины, например для правой, а на левой половине воспользоваться условием (1.126) в тот же момент времени.

Запишем граничное условие на поверхности пластины при x = δ :

∂ϑ			α
	∂		= −	ϑ	х=δ	при τ > 0 .	(1.128)

		х х=δ	λ

Решение дифференциального уравнения (1.124) с учетом условий однозначности даст искомое распределение температуры в плоской пластине.

Искомую функцию от двух переменных ϑ (τ , х) запишем в виде произведения функций ϕ (τ ) и ψ (х) :

ϑ = ϑ τ( , х=)ϕ τ (ψ ) (х) .

(1.129)

В результате подстановки выражения (1.129) в дифференциальное уравнение теплопроводности (1.124) получим

		∂ϕ	τ(	)	∂	ψ	2	(х)
ψ	(х)		∂τ	=	аϕ τ (	)			.	(1.130)
ψ	(х)		∂τ	=	аϕ τ (	)	∂	х2	.	(1.130)
										63

Обозначим ϕ ′(τ )=

∂ ϕ (τ )

и ψ′′(х) =

∂ 2 ψ(х)

. Тогда уравнение

∂ х2

(1.130) запишем ввиде

∂τ

φ′(τ)ψ(х) = аφ(τ)ψ′′(х) .

(1.131)

Послеразделения переменных уравнение(1.131) примет вид

φ′(τ)

ψ′′(х)

(1.132)

a φ(τ)

φ (х)

Из уравнения видно, что

φ′(τ)

= const

ψ′′(х)

= const.

a φ(τ)

φ (х)

Обозначив константу через −k 2 , перепишем уравнение (1.132):

	1	φ′(τ)	=	ψ′′(х)	= −k 2 .	(1.133)
			=		= −k 2 .	(1.133)
	a φ(τ)			φ (х)
Тогда
	φ′(τ) + ak 2φ(τ) = 0 ;					(1.134)
	ψ′′(x) + k 2 ψ(x) = 0 .					(1.135)
Решениями уравнений (1.134) и (1.135) являются функции
		φ(τ) = C1 e−ak 2 τ ;				(1.136)
ψ(x) = C2 sin(kx) + C3 cos(kx) .						(1.137)
После подстановки выражений (1.136) и (1.137) в уравне-
ние (1.129) получим
ϑ (x, τ) =ϑ = С1е−аk 2 τ C2 sin (kx) + C3 cos (kx) .						(1.138)

64

Для определения постоянных величин С1 ,						С2 , С3	и k вос-
пользуемся начальными и граничными условиями.
После подстановки граничного условия (1.127) на оси сим-
метрии в уравнение (1.138) имеем
	∂ ϑ	= С k e−аk	2 τ C		cos (0) − C sin (0) = 0 .		(1.139)
				2
		1			3
	∂ х	х=0

Из этого уравнения следует, что постоянная интегрирования C2 = 0 . Если обозначить C1C3 = A , то уравнение (1.138) примет вид

ϑ = Аe−аk 2 τ cos (kx) .

(1.140)

Продифференцировав уравнение (1.140) по координате x при x = δ, получим

∂ ϑ	= −kAe	−аk	2 τ	sin (kδ) .
					(а)

∂ х	х=δ

После подстановки граничного условия (1.128) в уравнение (1.138) имеем

∂ ϑ

−аk 2 τ

cos (kδ) .

х=δ

= −

Аe

(б)

∂ х

При равенстве левых частей уравнений (а) и (б) приравни-

ваем правые части:

−kAe−аk 2 τ sin (kδ ) = −

Аe−аk 2 τ cos (kδ) ,

(1.141)

откуда получаем

ctg (kδ) =

kδ

(1.142)

αδ

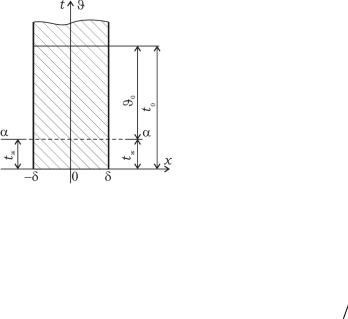
Если принять kδ = µ и αδλ = Bi , то выражение (1.142)

можно записать в виде

ctg (µ) =	µ	.	(1.143)

	Bi

Характеристическое уравнение (1.143) имеет бесконечное множество решений µ1 , µ2 , …, µn , … (рис. 1.17), причем

µ1 < µ2 <...< µn <...

y





y1=ctg µ	y1	y1	y2=µ/Bi

0	µ1	π µ2	2π µ3	3π

Рис. 1.17. К решению уравнения (1.143)

Каждому найденному корню µi					соответствует частное рас-
пределение температуры:
			x		2 aτ
ϑ i = Ai					−µi
					−µi		2
	cos	µi		e		δ		,	(1.144)
	cos	µi		e		δ		,	(1.144)
			δ

где i = 1, 2, ... , n, ...

Общее решение можно представить суммой бесконечного ряда частных распределений температуры:

∞

ϑ= ∑ Аi

i =1

		x		2 аτ
				−µi
				−µi		2
cos	µi		e		δ		.	(1.145)
cos	µi		e		δ		.	(1.145)
		δ

Постоянные Аi в уравнении (1.145) определяем из начального условия (1.125). При τ = 0 уравнение (1.145) имеет вид

∞	cos		x	.
ϑ 0 = ∑ Аi		µi			(1.146)
			δ
i=1

Уравнение (1.146) есть разложение четной функции в ряд Фурье с заданными параметрами µi , определяемыми из уравне-

ния ctg (µ) = µ . Bi

Для последовательности чисел µi можно записать соотношение


+δ		x			x

∫ cos	µi		cos	µm		dx

−δ		δ			δ

= 0,	i ≠	m,
=	i=	(1.147)
≠ 0,	i=	m,

с помощью которого можно определить коэффициенты Аi . Уравнение (1.146) после умножения левой и правой час-

тей на

cos

µm

dx ,

интегрирования по

и с учетом соотно-

шения (1.147) примет вид

+δ

∫ ϑ

= Am ∫ cos

0 cos

µm

dx ,

(1.148)

−δ

+δ

здесь ϑ 0 ∫ cos µm

dx = 2ϑ

sin µm .

µm

−δ

Поскольку	cos	2	µm
Поскольку	cos		µm

sin (2µm ) = 2sin (µm )cos (µm ) ,

= µδ (µm + sin (µm )cos (µm )) .

Тогда

x		1					x
	=		1	+ cos 2µm					и
		2
δ							δ	x
			+δ	1
то			∫		1	+ cos	2µm		dx =
				2				δ
			−δ

Аm = ϑ		2sin µm
	0		.
		µm + sin µm cos µm

Подставив (1.149) в уравнение (1.145), получим

∞

2sin µi

2 аτ

ϑ =

−µi

δ2

cos

∑ 0

µi + sin µi cos µi

i =1

(1.149)

(1.150)

Иногда бывает удобно уравнение (1.150) записать в безразмерном виде:

∞

2sin µi

)

Θ =

∑

cos

(

)

ехр−

µ2 Fo

, (1.151)

µi + sin µi cos

µi

(

i=1

где Θ = ϑ ϑ 0 ;

X = x δ; Fo= aτ δ2 – число Фурье, представляю-

щее собой безразмерное время.

Анализ полученного решения. Поскольку µ1 < µ2 <...<µn <...,

то каждый последующий член бесконечного ряда уравнения (1.151), меньше предыдущего. При увеличении числа Фурье Fo члены ряда будутубыватьбыстрее.

Результаты численных исследований показывают, что при Fo ≥ 0,3 распределение температуры с достаточной степенью точности описывается первым членом ряда уравнения (1.151):

		2sin µ1		(	1		)	(	1	)
Θ =	µ1	+ sin µ1 cos µ1	cos		µ	X		exp−	µ2 Fo		.	(1.152)
	µ1	+ sin µ1 cos µ1

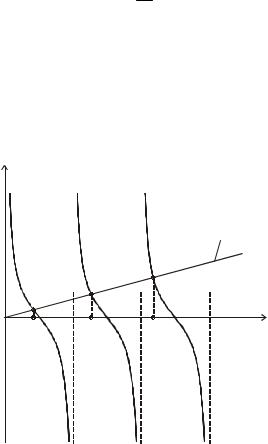
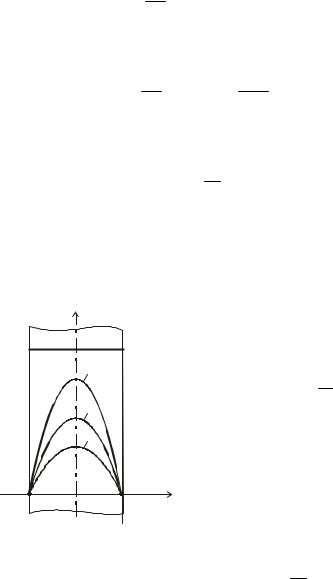
При охлаждении пластины (при τ = 0 ϑ ( x,0) =ϑ 0 ) в любой
момент времени зависимость температуры по координате x имеет
вид симметричной кривой с максимумом на оси пластины ( x = 0 ).
При этом касательные, проведенные						к	этим кривым в точках
X = ±1 , проходят через точки +A и −A , расположенные на рас-
стоянии ± X 0		от поверхности пластины,				Х0		=1 Bi (рис. 1.18).
					Θ
						Θ= 1; Fo= 0
								Fo1 > Fo
								Fo2 > Fo1
				X =0	X =1
			Θ		Θ
	−A		−1			1		ϕ	A X
			−1		0	1		ϕ	A X
		X0			0			X0
		X0						X0
	Рис. 1.18. Изменение температурного поляв плоской
		неограниченной стенкеприееохлаждении
Для того чтобы доказать это свойство, построим распре-
деление температуры в некоторый момент времени Fo>0 .
После		умножения		граничного		условия			третьего рода
∂ ϑ	α	х=δ на δ ϑ 0
∂ х х=δ	= − λϑ	х=δ на δ ϑ 0		получим
			∂ (ϑ ϑ	0 )	αδ	ϑ
			∂ ( х δ)		= − λ	ϑ	0	.	(1.153)
							0	х=δ
				х=δ				х=δ
После перехода к безразмерным переменным уравнение
(1.153) примет вид

∂Θ

= −BiΘ

X =1 .

(1.154)

∂ Х

Х =

Из рис. 1.18 следует, что

∂Θ

= tg φ =

X =1

(1.155)

−

X 0

∂ Х

Х =

Сравнивая уравнения (1.154) и (1.155), получаем

X 0

= 1 .

(1.156)

Из выражения (1.156) следует, что для заданных краевых

условий расстояние X 0

есть величина постоянная, не зависящая

от времени. Поэтому для любого момента времени касательные,

проведенные к температурным кривым в точках X = ±1 , будут

проходить через точки +A и −A .

Этот вывод справедлив и для тел

Θ= 1

Fo= 0

другихгеометрических форм.

Fo1

При Bi → ∞

(практически

при Bi >100 )

= 1 →

0 . Дан-

X 0

Fo2

ный режим охлаждения реализу-

Fo3

ется при

α → ∞ .

Граничное ус-

ловие третьего рода вырождает-

−A

ся в граничное условие первого

рода. Тогда распределение тем-

−1

ператур будет таким, как это по-

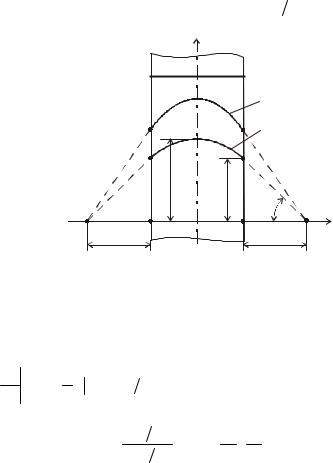
Рис. 1.19. Распределение

казано на рис. 1.19.

При Bi →

0 (практическипри

температуры вплоскойстенке

при ее охлаждениивусловиях

Bi < 0,1)

X 0

→ ∞ .

Малые

Bi → ∞

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20227.59 Mб12Теория технологических процессов учебное пособие..pdf
#
15.11.202219.88 Mб46Теория управления..pdf
#
15.11.20223.96 Mб28Теория электропривода учебное пособие..pdf
#
15.11.2022548.89 Кб3Теория электропривода..pdf
#
15.11.2022548.89 Кб3Теория электропривода.pdf
#
15.11.20224.77 Mб38Теплопередача учебное пособие..pdf
#
15.11.202210.8 Mб12Теплофизика в металлургии..pdf
#
15.11.20227.09 Mб13Теплофизические явления в полимерных материалах при интенсивном и кр..pdf
#
15.11.20221.69 Mб11Тестовый контроль по математике учебно-методическое пособие..pdf
#
15.11.202210.87 Mб21Техника технология и технические средства применяемые при реконстру..pdf
#
15.11.20221.1 Mб11Техника высоких напряжений..pdf