Теория электропривода учебное пособие

Здесь двигатель через соединительную муфту, редуктор

сдвухступенчатой зубчатой передачей, вторую соединительную муфту приводит во вращение барабан, преобразующий вращательное движение в поступательное перемещение груза

смассой mг со скоростью V через канат с массой mк. В подъемных установках с большой высотой (глубиной) подъема в переходных режимах на величину динамического усилия оказывает влияние переменная составляющая, как показано выше в уравнении (3.7). Для снижения динамических усилий в подъемной установке применяют (показано на рис. 3.1, а) систему уравновешивающих канатов, закрепленных одним концом к подъемному сосуду, другим – к барабану. Тогда суммарная масса груза в процессе подъема груза остается неизменной.

Таким образом, на рассматриваемой схеме видно, что в общем случае механическая часть электропривода представляет собой систему связанных масс, движущихся с различными скоростями вращательно или поступательно. При нагружении элементы системы (валы, опоры, зубчатые зацепления, канаты и т.п.) деформируются, так как механические связи не являются абсолютно жесткими. При изменениях нагрузки масса груза имеет возможность взаимного перемещения, определяемого жесткостью каната.

На расчетной схеме (рис. 3.1, б) моменты инерции и массы движущихся элементов показаны связанными упругими элементами с жесткостями сi, не имеющими механической инерции. В пределах деформаций упругих механических связей, для которых выполняется закон Гука, их жесткости можно определить с помощью соотношений

51

где Mi, i+1, Fj, j+1 – момент и нагрузка упругой механической связи;

∆ϕi и ∆Sj – деформация упругого элемента при вращательном (закручивание) и поступательном (перемещение) движениях элементов, ∆ϕi = φi – φi+1, ∆Sj = Sj – Sj+1.

Массы элементов и жесткости элементарных связей между ними в кинематической цепи привода различны. Определяющее влияние на движение системы оказывают наибольшие массы и наименьшие жесткости связей. Поэтому одной из первых задач при исследовании динамики электроприводов является составление упрощенных расчетных схем механической части, учитывающих возможность пренебрежения упругостью достаточно жестких механических связей и приближенного учета влияния малых движущихся масс.

Расчетную схему (см. рис. 3.1, б) можно существенно упростить вследствие малости некоторых ее моментов инерции. Для этого следует малые массы добавить к близлежащим большим, а затем определить эквивалентные жесткости связей между полученными массами. В результате получим трехмассовую систему, представленную на рис. 3.2.

Эквивалентные моменты инерции определены через массы элементов полной расчетной кинематической схемы

(см. рис. 3.1, б) как:

где

J123 = J1 + J2 + J3 ,

J45 = J4 + J5,

J2Σ = J6 + J7 + J8 + J9, mΣ = mг + mк .

52

В рассматриваемом примере движущиеся массы представлены тремя последовательно соединенными упругими элементами, состоящими из вала ротора двигателя с входным валом редуктора, промежуточного вала редуктора и выходного вала редуктора с валом барабана, а также упругой связью между грузом и двигателем в виде каната (см. рис. 3.2).

Рис. 3.2. Расчетная схема трехмассовой системы

Коэффициенты жесткости элементов (приведенные коэффициенты жесткости спр) должны быть эквивалентны реальным коэффициентам жесткости, поэтому при приведении жесткостей механических связей должно выполняться условие равенства запаса потенциальной энергии деформации упругих элементов в приведенной схеме с вращательным движением реальным условиям. Уравнение равенства запаса энергий приведенного элемента при упругой деформации вращательно движущегося реального элемента

∆φпр – приведенная угловая упругая деформация эквивалентного вала, рад.

53

Определим приведенные жесткости элементов для расчетной схемы трехмассовой системы, приведенной на рис. 3.2:

1) для упругой деформации каната с коэффициентом жесткости ск:

2) для упругой деформации вала барабана с коэффициентом жесткости с789:

спр2 = с789 i2 1i2 ; 1 2

3) для упругой деформации промежуточного вала с коэффициентом жесткости с5:

cпр1 = с5 i12 . 1

Полные кинематические схемы систем содержат элементы с разными жесткостями и схемами их соединения. Эквивалентные жесткости при последовательном и параллельном соединении элементов находят соответственно по выражениям

54

В расчетной схеме три последовательно соединенных элемента между массами J1 и J2 заменим одним упругим элементом, приведенная жесткость которого c12 определяется из соотношения

В трехмассовой системе, между массами которой есть упругие элементы (валы) с коэффициентами жесткости с12 и с23 = спр3, на каждую из вращающихся масс действуют движущие моменты и моменты сопротивления движению. На первую массу с моментом инерции J1 действует приложенный к ней движущий момент двигателя М, которому противодействует момент упругого закручивания вала M12 между первой и второй массами.

Величина этого момента определяется по формуле

все массы малых моментов вязкого и жесткого трения не учитывается.)

Движущим моментом, действующим на вторую массу, является момент упругого закручивания М12, а сопротивление оказывает момент упругого закручивания М23, определяемый аналогично моменту М12:

На третью массу с моментом инерции J3 действует движущий момент, являющийся моментом упругого закручива-

ния, M23, а моментом сопротивления является Mc3 = Mi сη.м ,

55

определяемый как приведенный к валу двигателя момент сопротивления движению, создаваемый в рабочей маши-

не, Мс.м.

Движение трехмассовой механической системы электропривода можно описать на основании (3.2) системой уравнений движения для каждой из вращающихся масс:

На рис. 3.3 представлена структурная схема, соответствующая системе уравнений (3.17).

Рис. 3.3. Структурная схема трехмассовой механической системы

Управляющим воздействием здесь является электромагнитный момент двигателя М, а возмущением – момент нагрузки Мс3. Регулируемыми переменными могут быть скорости ω1, ω2 и ω3, перемещения ϕ1, ϕ2 и ϕ3, а также нагрузки упругих связей М12 и М23. Структурно механическая часть электропривода представляет собой сложный объект, состоящий из цепочки интегрирующих звеньев, замкнутых перекрестными внутренними обратными связями.

Трехмассовая упругая система при исследовании электромеханических систем автоматизированного электропривода используется при детальном анализе динамики, иначе она сводится к двухмассовой.

56

Если передаточное устройство между третьей и второй массами является жестким c23 → ∞, то в нем не действует

момент M23, а ω2 = ω3.

В расчетной схеме двухмассовой упругой системы (рис. 3.4) суммарный приведенный момент инерции элементов, жестко связанных с двигателем, аналогично предыдущему обозначен J1. Суммарный приведенный момент инерции элементов, жестко связанных с рабочим органом механизма, обозначен J2. Безынерционная упругая связь между этими массами характеризуется приведенной эквивалентной жесткостью с12.

Рис. 3.4. Расчетная схема двухмассовой системы

Тогда математическое описание движения двухмассовой механической системы электропривода будет

и соответствующая ей структурная схема будет иметь вид, представленный на рис. 3.5.

Рис. 3.5. Структурная схема двухмассовой системы

57

Электромеханическая система с двухмассовой упругой механической частью представляет собой простейшую модель электропривода, наиболее удобную для изучения влияния упругих механических связей.

Если коэффициент жесткости с12 → ∞, то ω2 = ω1 = ω, J = J1 + J2 + J3, и структурная схема трехмассовой системы преобразуется к схеме одномассовой системы. Такая система обладает свойствами абсолютно жесткой механической сис-

Динамические характеристики (временные и частотные) такой системы соответствуют характеристикам идеального интегрирующего звена. При приложении нагрузки Mc = const скорость в такой системе изменяется по линейному закону.

3.3. Механическая часть электропривода как объект управления

Анализ динамических свойств механической части электропривода проводят решением уравнения движения электропривода как объекта управления по принятым расчетным схемам, исследуя переходные режимы.

Переходным процессом электропривода как динамической системы является режим его работы при переходе от одного установившегося состояния к другому, когда изменяется ток, момент и скорость двигателя.

Детальный анализ свойств упругих механических систем обычно проводят на основе двухмассовой расчетной схемы. Для устранения перекрестной связи в структурной схеме, приведенной на рис. 3.5, выполним ее преобразование

58

переносом внутренней связи по упругому моменту на выход системы.

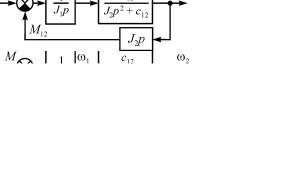
Определим передаточные функции системы, связывающие между собой скорости ω2 и ω1, а также скоростей ω2 и ω1 с электромагнитным моментом двигателя М по полученной структурной схеме (рис. 3.6).

Рис. 3.6. Преобразованные структурные схемы

59