Промышленные роботы Ч. 2 учебное пособие

зования координат [1, 2], которые отличаются друг от друга правилами выбора осей локальных систем координат, для манипуляторов обычно используется метод Дж. Денавита и Р. Хартенберга.

Опишем два вида матриц:

–матрицы М, определяющие отношение между системами координат соседних звеньев;

–матрицы Т, определяющие положение и ориентацию каждого звена механизма в неподвижной или базовой системе координат.

Воспользуемся однородными координатами трехмерного проективного пространства РR3, в которых движение евклидова пространства R3 можно представить линейным преобразованием

, (4.10)

и rj – радиус-вектор соответственно в новой и старой системах коорди-

носа.

поворот, определяемый матрицей Uij размерностью 3 3, и параллельный перенос, задаваемый вектором b размерностью 3. В однородном пространстве положение точки будут определять не три x, y и z, а четыре величины x', y', z' и t', которые удовлетворяют следующим соотношениям:

x = x'/t', y = y'/t', z = z'/t'.

Обычно принимают t'=1. У матрицы поворота Uij элементами uij являются направляющие косинусы углов между новой осью i и старой осью j. Вектор b x, y, z является трехмерным и определяет положение начала новой систе-

мы координат i в старой системе j.

Выбор расположения и ориентации локальных систем координат должен соответствовать типу решаемой задачи (прямая или обратная).

При использовании метода Денавита – Хартенберга оси координат располагаются по следующим правилам:

1. Для звена i ось zi направляется по оси кинематической пары, образуемой им со звеном (i+1). Начало координат размещают в геометрическом центре этой пары.

111

2. Ось xi направляется по общему перпендикуляру к осям zi-1 и zi с направлением от zi-1 к zi. Если оси zi-1 и zi совпадают, то xi перпендикулярна к ним и направлена произвольно. Если они пересекаются в центре кинематической пары, то начало координат располагается в точке пересечения, а ось xi направляется по правилу векторного произведения xi zi zi 1 (кратчайший поворот

оси zi до совмещения с zi-1 при наблюдении с конца xi должен происходить против часовой стрелки).

3. Ось yi направляется так, чтобы система координат была правой.

Впрямой задаче необходимо определить положение схвата манипулятора

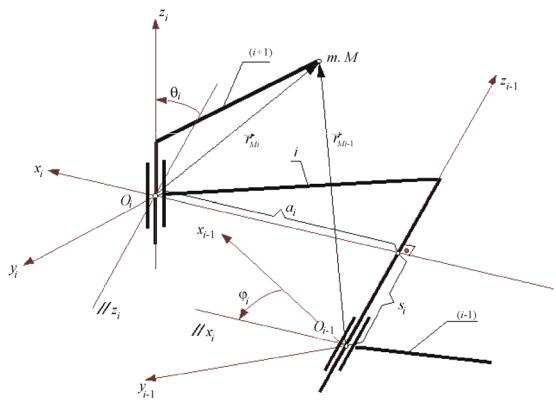
исвязанной с ним системы координат xnynzn по отношению к неподвижной (базовой) системе координат x0y0z0. Это осуществляется последовательными переходами из системы координат звена i в систему координат звена (i–1). Согласно принятому методу, каждый переход включает в себя последовательность четырех движений – двух поворотов и двух параллельных переносов, осуществляемых в указанной последовательности (рис. 4.19):

–поворот i-й системы вокруг оси xi на угол i до параллельности осей zi

иzi-1 (положительное направление поворота при наблюдении с конца вектора xi против часовой стрелки);

–перенос вдоль оси xi на величину ai до совмещения начала системы координат Oi с точкой пересечения осей xi и zi-1 (отсчитывается по оси xi от точки пересечения оси xi и оси zi-1);

Рис. 4.19. Последовательность расчета прямой задачи кинематики

112

–перенос вдоль оси zi-1 на величину si, после которого начало системы координат Oi оказывается в начале координат Oi-1 системы (i–1) (отсчитывается по оси zi-1 от ее начала координат Oi-1 до точки ее пересечения с осью xi);

–поворот вокруг оси zi-1 на угол i до тех пор, пока ось xi не станет параллельной оси xi-1 (положительное направление поворота при наблюдении с конца вектора zi-1 против часовой стрелки).

Необходимо отметить, что знак угла поворота не имеет значения, так как в матрицах перехода используются направляющие косинусы (четные функции). Целесообразно рассматривать угол, обеспечивающий кратчайший поворот оси старой системы i до совмещения (параллельности) с соответствующей осью новой (i–1). Перемещения начала координат определяются как координаты начала Oi старой системы в новой.

В манипуляторах обычно используются одноподвижные вращательные или поступательные кинематические пары. Оба относительных движения, как вращательное, так и поступательное, реализуются в цилиндрических парах. Поэтому при общем представлении механизма (см. рис. 4.19) используются цилиндрические пары. Матрицы перехода из системы i в систему (i–1) можно записать так:

113

В этих матрицах переменные si и i соответствуют относительным перемещениям звеньев в кинематических парах и являются обобщенными координатами манипулятора, определяющими конфигурацию механизма в рассматриваемом положении. Переменные ai и i определяются конструктивным исполнением звеньев манипулятора, в процессе движения они остаются неизменными.

Положение некоторой произвольной точки М в системе координат звена i

определяется вектором rMi, а в системе координат звена (i–1) – вектором rMi 1. Эти радиусы связаны между собой через матрицу преобразования координат Мi

Рассмотрим шестиподвижный манипулятор в исходном или начальном положении (рис. 4.20). За начальное положение принимается такое, в котором все относительные обобщенные координаты равны нулю.

Рис. 4.20. Кинематика шестиподвижного манипулятора: 0–6 – звенья манипулятора

114

Переход из системы координат любого i-го звена к неподвижной (базовой)

где Ti – матрица преобразования координат i-й системы в координаты базовой

системы координат, i M1 M2 ...Mi .

Для схемы, изображенной на рис. 4.20, радиус rM 6 0, а радиус rM 0 опре-

деляется по формуле

rM 0 n 6 ,

т.е. положение выходного звена манипулятора определяется матрицей Тn. Элементы этой матрицы определяют положение центра схвата (точки М) и ориентацию его в пространстве. Четвертый столбец определяет декартовы координаты точки М (проекции вектора rM 0 на оси координат). Третий столбец содержит

направляющие косинусы оси zn системы координат, связанной со схватом, или

вектора подхода A, который характеризует направление губок схвата

(рис. 4.21). Второй столбец определяет направление оси yn или вектора ориен-

тации O, который проходит через центр схвата по оси, перпендикулярной ра-

115

В результате матричных преобразований получаем радиус-вектор точки М схвата в функции обобщенных координат. Обычно за обобщенные координаты принимают линейные и угловые перемещения в кинематических парах или на выходных валах приводов манипулятора. В механизме с n степенями подвижности в общем виде функцию положения схвата можно записать так:

где q1, q2,...,qn – обобщенные координаты манипулятора.

Другая задача кинематического анализа – определение скоростей. В прямой задаче необходимо определить линейные и угловые скорости и ускорения схвата при заданных угловых и линейных обобщенных скоростях и ускорениях (обычно относительных скоростях и ускорениях в кинематических парах механизма). В обратной задаче по заданному закону изменения скоростей и ускорений схвата определяются законы изменения скоростей и ускорений в КП или на выходных звеньях приводов.

Решение прямой задачи кинематики для точки М схвата можно получить, продифференцировав четвертый столбец матрицы Тn по времени:

Угловую скорость и угловое ускорение схвата можно определить векторным суммированием относительных угловых скоростей во вращательных КП механизма. Так как векторы угловых скоростей, при данном выборе ориентации осей координат, совпадают с осью z, то угловая скорость схвата

щей звено i и звено (i–1), m – число вращательных КП в механизме.

116

Дифференцируя это выражение по времени, получим формулу для определения углового ускорения схвата:

4.5.3. Решение задач кинематики векторным методом

Решение прямой задачи о положениях рассмотрим на примере манипуля-

тора с тремя вращательными кинематическими парами.

Заданными будем считать обобщенные координаты механизма, за которые приняты углы относительного поворота звеньев в кинематических парах. Для решения задачи мысленно установим манипулятор в некоторое нулевое положение, в котором все обобщенные координаты равны нулю.

Положение манипулятора в любой момент времени определяется ориента-

цией осей его звеньев и кинематических пар и их положением. В нулевом по-

ложении векторы, направленные по осям звеньев и кинематических пар, считаем известными. Чтобы перевести манипулятор из нулевого положения в положение, задаваемое обобщенными координатами i i 1,...,3 , совершим последователь-

ные повороты в шарнирах на углы i , начиная с неподвижного звена (рис. 4.22).

Рис. 4.22. Кинематика манипулятора с тремя подвижными парами

Первый поворот совершим в шарнире А на угол φ1 вокруг единичного вектора k. При этом векторы изменят свое положение и перейдут в векторы

i2(1) ,i3(1) .

117

Эти векторы могут быть найдены по формуле Родриго:

(4.19)

где i ,k – единичные векторы (орты) декартовой системы координат, s – число осей единичного вектора, s = 2; 3.

Ввиду того, что векторы коллинеарны между собой и ортогональны вектору k, член, содержащий три вектора в формуле (4.19), равен нулю; с учетом этого получим:

После определения векторов, задающих положения векторов и звеньев, легко находятся радиусы-векторы точек механизма:

Найденные векторы полностью определяют абсолютное положение манипулятора в пространстве.

Прямая задача о скоростях состоит в определении абсолютных линейных скоростей точек звеньев манипулятора и абсолютных угловых скоростей звень-

118

ев при заданных законах изменения обобщенных координат qi(t) (i=l,2,...,n, где n – число степеней свободы манипулятора).

Так как радиус-вектор произвольной точки звена манипулятора представляет собой вектор-функцию обобщенных координат qk , то можно записать выражение для линейной скорости точки звена:

Для решения задачи используем метод приведения скоростей. Считаем, что в каждой кинематической паре манипулятора совершается одно движение: вращательное или поступательное. Считаем также, что относительные движения в каждой кинематической паре заданы, а требуется изучить движение звеньев манипулятора в неподвижной системе координат. Очевидно, что при одновременном движении во всех кинематических парах происходит сложение нескольких движений твердого тела. В качестве примера рассмотрим сложение двух движений.

Пусть два звена входят в одну кинематическую пару. С каждым из звеньев свяжем системы координат ( 1x1 y1z1 и 2 x2 y2 z2 ). Пусть первое звено и связанная с ним система координат 1x1 y1z1 совершает переносное движение по отношению к системе xyz, а система 2 x2 y2 z2 совершает относительное движение по отношению к системе 1x1 y1z1 . Тогда для произвольной точки М второго

звена скорость может быть найдена по формуле сложения скоростей: vM v1 v2 ,

где v1 – скорость точки первого звена, с которой в данный момент времени совпадает точка М второго звена; v2 – скорость точки второго звена относи-

тельно первого звена.

Так как от перестановки слагаемых в этой формуле суммарный вектор не изменяется, то относительное и переносное движения можно поменять местами.

Если число подвижных звеньев и кинематических пар увеличить на единицу, то найденную скорость точки М звена 2 можно принять за переносную при определении скорости точки М звена 3, т.е. скорость точки конечного звена равна сумме скоростей этой точки при движении в каждой кинематической па-

i 1

Если все кинематические пары поступательные, то скорости всех точек конечного звена равны сумме линейных относительных скоростей.

119

Если какая-либо из n кинематических пар вращательная, то соответствующая ей

где i – вектор относительной угловой скорости во вращательной паре i; rin – ра- диус-вектор, задающий положение точки М звена n относительно центра пары i.

4.6.Динамика манипулятора

4.6.1.Методы построения динамической модели манипулятора

Динамическая модель манипулятора может быть построена на основе использования известных законов ньютоновской или лагранжевой механики. Результатом применения этих законов являются уравнения, связывающие действующие в сочленениях силы и моменты с кинематическими характеристиками и параметрами движения звеньев. Таким образом, уравнения динамики движения реального манипулятора могут быть получены традиционными методами Лагранжа – Эйлера или Ньютона – Эйлера. С помощью этих двух методов получен ряд различных форм уравнения движения, эквивалентных в том смысле, что они описывают динамику движения одной и той же физической системы.

Вывод уравнений динамики движения манипулятора методом Лагранжа – Эйлера отличается простотой и единством подхода. В рамках предположения о том, что звенья представляют собой твердые тела, этот подход приводит в общем случае к системе нелинейных дифференциальных уравнений второго порядка. Уравнения Лагранжа – Эйлера обеспечивают строгое описание динамики состояния манипулятора и могут быть использованы для разработки усовершенствованных законов управления в пространстве присоединенных переменных. В меньшей степени они используются для решения прямой и обратной задач динамики. Прямая задача состоит в том, чтобы по заданным силам и моментам определить обобщенные ускорения, интегрирование которых позволяет получить значения обобщенных скоростей и координат. Обратная задача динамики заключается в том, чтобы по заданным обобщенным координатам, скоростям и ускорениям определить действующие в сочленениях манипулятора силы

имоменты.

Сцелью получения более эффективных с вычислительной точки зрения алгоритмов можно использовать уравнения Ньютона – Эйлера. Вывод уравнений движения манипулятора методом Ньютона – Эйлера прост по содержанию,

120