Промышленные роботы Ч. 2 учебное пособие

–уравновешивание механизмов манипуляторов;

–другие задачи.

Эти задачи решаются на базе общих методов исследования структуры, геометрии, кинематики и динамики систем с пространственными многоподвижными механизмами. Каждая из рассматриваемых задач может быть сформулирована как прямая (задача анализа) или как обратная (задача синтеза). При определении функций положения механизма в прямой задаче находят закон изменения абсолютных координат выходного звена по заданным законам изменения относительных или абсолютных координат звеньев, в обратной – по заданному закону движения схвата находят законы изменения координат звеньев, обычно линейных или угловых перемещений в приводах. Решение обратной задачи, или задачи синтеза, более сложно, так как часто она имеет множество допустимых решений, из которых необходимо выбрать оптимальное. В обратной задаче кинематики по требуемому закону изменения скоростей и ускорений выходного звена определяются соответствующие законы изменения скоростей и ускорений в приводах манипулятора. Обратная задача динамики заключается в определении закона изменения управляющих сил и моментов вприводах, обеспечивающих заданный закон движения выходного звена.

4.3. Структурный анализ манипулятора

Структурный анализ манипулятора заключается в разложении его на составляющие. В состав манипулятора входят: основной механизм, передаточные механизмы, механизмы захватных устройств, механизмы уравновешивания и развязки движений.

Механизмы передачи движения от двигателей к основным звеньям могут быть: рычажные, зубчатые, мальтийские, шарнирно-винтовые, волновые и т.д.

Уравновешивание сил тяжести моментов инерции звеньев манипулятора и объекта манипулирования может быть достигнуто с помощью противовесов, упругих элементов, приводных двигателей или рационального распределения масс звеньев. В манипуляторе число входных звеньев равно числу приводов, а выходное звено одно – схват или рабочий орган.

Основной механизм манипулятора является незамкнутой пространственной кинематической цепью, состоящей из звеньев (рис. 4.12). Число степеней свободы манипулятора равно числу обобщенных координат, под которыми понимают независимые данные, однозначно определяющие положение его звеньев в пространстве.

101

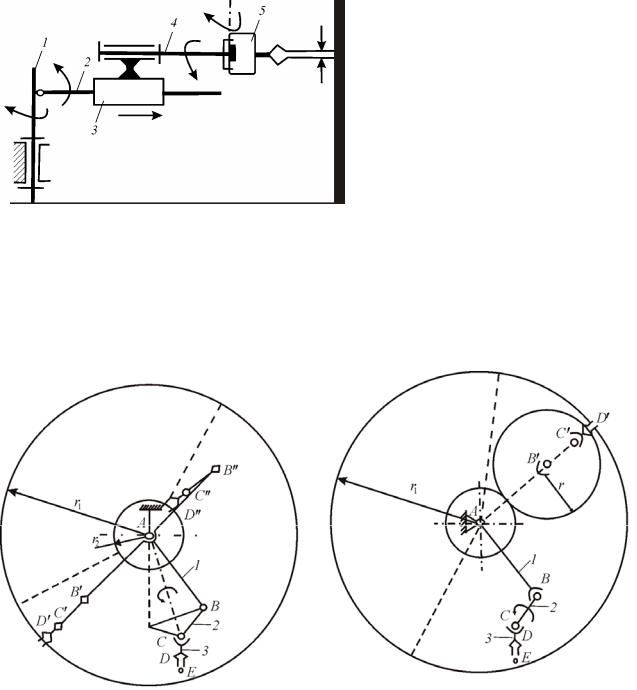
Рассмотрим подробнее основные геометрические и структурные характеристики манипуляторов, к которым прежде всего относятся число степеней подвижности, маневренность, угол и коэффициент сервиса, форма и размеры рабочей зоны в крайних его положениях

(рис. 4.13).

Число степеней подвижности схвата манипулятора можно подсчитать как сумму подвижностей всех пар открытой кинематической цепи. Сказанное не противоречит формуле Малышева для пространственных механизмов, так как в открытых цепях число подвижных звеньев всегда равно числу кинематических пар.

Рис. 4.13. Манипулятор с тремя подвижными кинематическими парами:

а – рабочая зона в начале рабочего хода; б – рабочая зона в конце рабочего хода

Для манипуляторов на рис. 4.13 с одноподвижными парами

W 6 n 5 p5 6 3 5 3 3,

где п – число подвижных звеньев; р5 – число одноподвижныхпар. Маневренность характеризует возможность кинематической цепи манипу-

лятора занимать разные положения при одном и том же положении схвата. Она зависит не только от вида и числа кинематических пар, но и от их расположения. Так, манипулятор, изображенный на рис. 4.13, а, имеет маневренность,

102

равную единице. Групповая подвижность означает возможность совместного вращения звеньев 1, 2 вокруг оси АС, проходящей через центры сферических пар. Если маневренность равна единице, то к заданной точке Е в заданном направлении СЕ схват может подойти при различных положениях остальных звеньев 1, 2, геометрическим местом которых будут конические поверхности с вершинами в точках А и С и образующими АВ и СВ.

Если пары А и В поменять местами (рис. 4.13, б), то число степеней подвижности, согласно формуле Малышева, останется прежним:

W 6 n 6 i p1 6 2 5 1 3 2 1.

Но это местная подвижность, означающая возможность вращения звена 2 вокруг оси ВС. При этом маневренность будет равна нулю, поскольку в данном случае схват может подойти к заданной точке Е рабочей зоны в заданном направлении СЕ только при одном единственном положении звеньев 1, 2.

Повышенная маневренность увеличивает возможности для выполнения сложных операций с объектом манипулирования наиболее рациональным путем в условиях наличия препятствий в рабочей зоне, но усложняет задачу управления таким роботом, поскольку приводит к неоднозначному решению задачи расчета обобщенных координат.

В соответствии с ГОСТ 25686–85 рабочее пространство манипулятора –

часть физического пространства, в котором может находиться исполнительное устройство при функционировании манипулятора.

Рабочая зона – пространство, в котором может находиться рабочий орган. Не в любой точке рабочей зоны схват может занимать произвольное положение из-за конструктивных ограничений на углы поворота в шарнирах, поэтому рабочая зона реально уменьшается до зоны обслуживания.

Зона обслуживания – пространство, в котором рабочий орган выполняет свои функции в соответствии с назначением.

Для манипулятора, изображенного на рис. 4.13, а, рабочая зона – это пространство между сферами радиусом r2 = AD" и радиусом r1 = AD', а зона обслуживания лишь часть такого пространства (отделенная штриховой линией на рис. 4.13, а); для манипулятора, изображенного на рис. 4.13, б, рабочая зона – тор (кольцо кругового сечения) с размерами r1 = AD' и r = В' D', а зона обслуживания – часть такого тора (отделенная штриховой линией на рис. 4.13, б).

103

Манипулятор с тремя поступательными парами имеет рабочую зону в виде прямоугольного параллелепипеда. Для манипулятора с одной вращательной и двумяпоступательнымипарами рабочаязона– кольцевойцилиндрическийсектор.

Для каждой точки рабочей зоны можно определить угол сервиса , внутри которого схват может подойти к этой точке. Как известно, величина телесного угла определяется отношением площади сферы, вырезанной телесным углом, к квадрату радиуса сферы, поэтому максимальное значение угла сервиса

max 4r2r2

Отсюда коэффициент сервиса в данной точке равен отношению угла к его максимальному значению, т.е. k /(4 ). Величина может изменять-

ся от нуля для точек на границе рабочей зоны, где схват может быть подведен в единственном направлении, до единицы для точек зоны полного сервиса, где схват может быть подведен в любом направлении.

Определение значения коэффициента сервиса k связано с анализом дви-

жения звеньев механизма манипулятора при различных фиксированных положениях центра схвата.

Методику вычисления k рассмотрим на примере манипулятора с двумя

сферическими и одной вращательной парами (см. рис. 4.13, а). Для определения угла сервиса в некоторой точке Е рабочей зоны рассмотрим механизм манипулятора как пространственный четырехзвенник со сферическими парами А, С, D и вращательной парой В; точка D центра схвата совпадает с заданной точкой Е на линии 4 (рис. 4.14, а). Сперва определим возможные положения звена CD (схвата) в плоскости чертежа, а затем все его возможные положения в пространстве путем вращения плоского четырехзвенника относительно условной стойки AD длиной r, совпадающей с осью х пространственной системы координат.

В области, где коэффициент сервиса k = 1, угол сервиса = 4π. Следова-

тельно, точка С должна иметь возможность занять любое положение на сфере радиусом DC = l3 с центром в точке D. Для этого в плоском четырехзвеннике звено CD должно быть кривошипом, т.е. поворачиваться на полный оборот. Известное условие существования кривошипа состоит в том, что сумма длин самого короткого и самого длинного звеньев должна быть меньше суммы длин

104

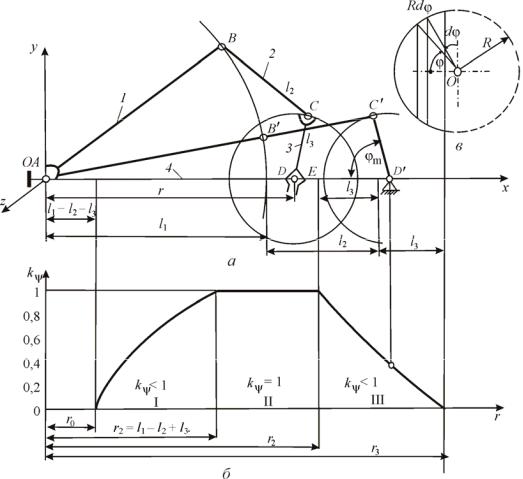
остальных звеньев. Если, например, звено 1 самое длинное, а звено 3 самое короткое, то l1 + l3 < r + l2, откуда rmin = r1 = l1 – l2 + l3 (рис. 4.14, б).

Рис. 4.14. Механизм манипулятора со сферическими и вращательной парами

Если самое длинное звено AD = r, а самое короткое звено 3, то r + l3 < l1 + l2,

откуда rmах = r2 = l1 + l2 – l3.

В пределах от rх до r2 коэффициент сервиса k = 1 (см. рис. 4.14, б, зона II). Еcли же звено 3 является коромыслом, то k < 1. В предельных положениях, когда звенья 1, 2, 3 находятся на одной прямой Ах, k = 0. Это имеет место

при r = r0 = l1–l2–l3 и при r = r3 = l1 +l2 +l3. Следовательно, в зонах I и III

на рис. 4.14, б k < 1.

В любой промежуточной точке зон I или III, например в точке D', можно определить коэффициент сервиса следующим образом. Найдя максимально возможный угол поворота m коромысла C'D', когда звенья АB' и В'С' находят-

ся на одной прямой, определим поверхность сферического сектора радиусом R и углом φ = φm (рис. 4.14, в). Формулу поверхности S шарового сектора получим путем суммирования элементарных поверхностей dS = 2RsinφRdφ в пределах от φ = 0 до φ = φm:

105

изображенными на рис. 4.14, а, представлен на рис. 4.14, б. Подобные графики нужны не только при исследовании имеющегося манипулятора, но и при проектировании кинематических схем манипуляторов по заданным условиям.

К техническим характеристикам манипулятора также относятся грузоподъемность, быстродействие, точность позиционирования, энергетические затраты и т.д.

4.4. Структурный синтез механизма манипулятора

Структурный синтез манипулятора заключается в проектировании его структурной схемы по заданным условиям: типу, числу степеней свободы, виду движения перемещаемого объекта. Главной задачей структурного синтеза является выбор числа звеньев, класса и порядка расположения кинематических пар.

В зависимости от назначения манипулятора выбирают различные варианты синтеза его механизма. Например, манипулятор, показанный на рис. 4.15, действует в сферической (или полярной) системе координат. Его схват может выдвигаться и втягиваться. Вертикальные перемещения манипулятора достигаются путем поворота его в вертикальной плоскости и «плечевом» суставе. Весь узел

манипулятора может также поворачиваться вокруг оси основания. Зона действия такого манипулятора представляет собой усеченную сферу. Первые модели промышленных роботов были сконструированы именно по этому принципу.

Шарнирный манипулятор (рис. 4.16), действующий в ангулярной системе координат, не имеет поступательных кинематических пар, а имеет только вращательные кинематические пары. Манипулятор такого типа очень напоминает руку человека, поскольку имеет «плечевое» и «локтевое» сочленения, а также

106

«запястье». Его зона обслуживания значительно больше, чем роботов других типов. Он способен обходить препятствия гораздо более разнообразными путями и даже складываться, но вместе с тем он исключительно сложен в управлении.

Манипулятор системы SCARA (рис. 4.17), имеющий своеобразную схему, представляет собой вариант манипулятора с цилиндрической системой координат. Все кинематические пары этого манипулятора располагаются в горизонтальной плоскости, благодаря чему механизм способен разворачиваться подобно складной ширме. Его зона обслуживания имеет цилиндрическую форму.

Перспективным представляется манипуляционный механизм системы «Spine» (рис. 4.18), спро-

ектированный специалистами фирмы «Спайн роботикс». В нем используется длинный хоботоподобный манипулятор, состоящий из множества чечевицеобразных дисков, которые соединены между собой двумя парами тросов, обеспечивающих натяжение. Тросы соединены с поршнями гидравлических цилиндров, которые, создавая

натяжение, вызывают перемещение манипулятора. Специальные датчики передают в систему управления информацию о положении манипулятора и его кисти. Такой манипулятор отличается большой гибкостью, значительным радиусом действия и высокой маневренностью.

107

4.5.Кинематика механизма манипулятора

4.5.1.Методы решения задач кинематики

Исследование кинематики манипуляторов является одним из важных этапов проектирования манипуляторов. На этом этапе производится стыковка геометрических характеристик проектируемых модулей и манипулятора в целом с рабочим пространством и рабочей зоной робота; определяются возможности манипулятора с точки зрения кинематики при выполнении тех или иных технологических операций; учитываются различные неблагоприятные факторы, например упругая податливость элементов. Результаты таких исследований обычно используют для корректировки конструкторских решений, принятых на предыдущих этапах проектирования. Кроме того, они необходимы в дальнейшем при проектировании системы управления роботом, так как на их основе строится модель робота как объекта управления.

Для постановки и решения задач кинематики обычно составляют расчетную кинематическую модель манипулятора, в основу которой должны быть положены предполагаемые или имеющиеся геометрические размеры звеньев, а также типы, количество и распределение кинематических пар.

Манипулятор обычно представляет собой открытую кинематическую цепь, элементы которой соединены друг с другом посредством кинематических пар. Как правило, это одноподвижные кинематические пары пятого класса, вращательные либо поступательные. Если кинематическая цепь не содержит внутренних замкнутых контуров, то число кинематических пар определяет число степеней подвижности манипулятора. Простейшие манипуляторы имеют дветри степени подвижности. Универсальные, а также некоторые специальные манипуляторы могут иметь шесть-восемь степеней подвижности.

Звенья кинематической цепи соединены кинематическими парами так, что одно из них крепится к основанию (подвижному или неподвижному), а еще одно несет на себе рабочий орган – схват или инструмент.

Наиболее характерные задачи кинематики манипуляторов – это прямые и обратные задачи о положениях и скоростях. Для пространственных механизмов наиболее эффективными методами решения этих задач являются матричный метод преобразования координат и векторный метод, основанный на использовании формул конечного поворота твердого тела.

Матричный метод преобразования координат вектора. Рассмотрим три декартовы системы координат: xyz , 1x1 y1z1 , 2 x2 y2 z2 . Пусть в системе

108

2 x2 y2 z2 заданы координаты вектора r (х2, у2, z2). Тогда в системе 1x1 y1z1 координаты этого же вектора могут быть определены в матричной форме следующим образом:

2 x2 y2 z2 , x2 x2 , y2 , z2 (индекс «Т» означает операцию транспонирования матрицы); L2 – матрица перехода от системы 2 x2 y2 z2 к системе 1x1 y1z1 ,

Элементы αij (i, j = 1, 2, 3) матрицы L1 есть направляющие косинусы осей системы 1x1 y1z1 относительно осей системы xyz .

Проведя некоторые преобразования в выражениях (4.5) и (4.6), получим:

i 1

где xn – матрица-столбецкоординатвектора r всистеме n xn yn zn , xn xn , yn , zn ;

n

L1 L1L2...Ln.

i 1

109

Метод, основанный на использовании формул конечного поворота твердого тела. Этот метод позволяет определить новое положение вектора, зная его старое положение, ось поворота и угол поворота.

Рассмотрим различные формулы конечного поворота твердого тела. По формуле Родриго:

В этом случае получим:

r1 = r 11 22 e r e 1 2 2 e r 1 2 2 .

Если угол между осью и вектором r равен 90°, то формула упрощается

и принимает вид

r1 r cos e r sin .

При совершении двух конечных поворотов тела вокруг осей, определяе-

Последняя формула показывает, что результирующий поворот двух конечных поворотов твердого тела вокруг неподвижных осей зависит от порядка выполнения этих поворотов.

4.5.2. Решение задач кинематики методом преобразования координат

Первая и основная задача кинематики – определение функции положения. В прямой задаче о положениях необходимо определить положение выходного звена как функцию перемещений в приводах, в обратной – перемещения в приводах как функцию заданного положения выходного звена.

При решении прямой задачи о положении схвата манипулятора обычно используют метод преобразования координат. Из множества методов преобра-

110