
Математические модели движения транспортных средств
..pdf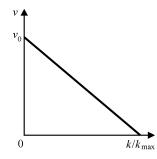
и, следовательно, количество автомобилей на отрезке дороги (x1, x2) постоянно для любых значений t ≥ 0.
Уравнение (2.18), впервые полученное Гриншилдсом, носит его имя. Линейная аппроксимация Гриншилдса представлена на рис. 2.1.
Можно построить макроскопическую модель, в которой уравнение Гриншилдса является частным случаем. Рассмотрим связь между скоростью v и
плотностью k автомобилей на дороге. В общем случае, когда плотность k повышается, водители снижают скорость и наоборот, поэтому
v = v{k x(t), |
t }, |
(2.21) |
|
|
|
где x(t) – координата движения элемента потока.
Проследим изменение скорости для некоторого передвигающегося элемента потока во времени, которое определяется как полная производная по времени:
dv |
= |
dv |
∂k |
+ |
dv |
∂k dx. |
dt |
|
|
||||
|
dk ∂t |
|
dk ∂x dt |
|||
Из уравнения (2.16) следует соотношение
∂∂kt = −k ddvx −v ∂∂kx ,
которое после подстановки в (2.22) принимает вид
(2.22)
(2.23)
dv |
= −k |
dv dv |
−v |
∂k dv |
+v |
∂k dv |
= −k |
dv dv |
(2.24) |
||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
||||||||||||||
|
dx dk |
|
∂t dk |
|
∂t dk |
|
dx dk |
|
|||||||||
Поскольку в соответствии с уравнениям (2.21)
dv |
= |
dv |
dk |
, |
(2.25) |
dx |
|
||||
|
dk dx |
|
|
||
|
|
|
|
|
31 |

из соотношения (2.24) получаем
dv |
dv 2 |
∂k |
= −k (v′) |
2 |
∂k |
|
|
||
|
= −k |
|
|
∂x |
|
∂x |
, |
(2.26) |
|
|
|
|
|||||||
dt |
dk |
|
|
|
|
||||
где v′= dv dk , а отрицательный коэффициент пропорциональности |
|||||||||
−k (v′)2 |
|
можно интерпретировать как вязкость в жидкости. Для |
|
|
|
классической сжимаемой жидкости уравнение (2.26) называется уравнением Эйлера, в этом случае
dv |
= −C2k−1 ∂k |
, |
(2.27) |
dt |
∂x |
|
|
где С – неотрицательная константа с размерностью скорости. Принято рассматривать более общий класс моделей, в которых
dv |
= −C2kn ∂k . |
(2.28) |
dt |
∂x |
|
Уравнение (2.27) соответствует случаю n ≠ –1, следовательно, из
уравнений (2.26) и (2.27) v′=C2k(n−1) 2 . Решением этого уравнения будет
2 . Решением этого уравнения будет
|
v = −C ln |
kmax |
|
|
|
|
(2.29) |
|||
при n = –1 |
k |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
v = |
C |
k( |
) |
2 |
−k( |
) |
2 |
|
, |
(2.30) |
|
|
|
n+1 |
|
n+1 |
|
|
|
||
|
|
max |
|
|
|
|
|
|
|
|
|
n +1 |
|
|
|
|
|
|
|||
при n ≠ –1.
Формула (2.29) впервые получена Гринбергом и носит его имя. Обозначив v0 скорость при k = 0, для значений n ≤ 0 можно записать
|
|
|
|
|
( |
) |
|
|
|
|
|
|
k |
|
|
n+1 |
2 |
|
|
v = v0 |
1− |
|
|
|
|
|
. |
(2.31) |
|
|
|
|
|
||||||
|
|
kmax |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Следует отметить, что полученное ранее уравнение Гриншилдса (2.18) является частным случаем уравнения Гринберга (2.31) при n = 1.
32

Кинематические волны в транспортном потоке
Зависимость интенсивности движения от плотности называют фундаментальной диаграммой транспортного потока. Эта диаграмма может быть получена по модели Лайтхилла-Уизема при следующих допущениях:
•транспортный поток непрерывен, его плотность k(x, t) есть число машин, занимающих единицу длины дороги;
•интенсивность движения q(x, t) равна числу машин, пересекающих черту x за единицу времени, определяется локальной плотностью k:
q =Q(k); |
(2.32) |
•скорость потока v(k) = Q(k) q , т.е. средняя скорость являет-
ся функцией плотности v(x,t) = vв (k (x,t));
• на участке дороги без съездов-въездов количество машин сохраняется.
Уравнения (2.32) и (2.19) образуют полную систему. После подстановки получим
∂k |
+c(k)∂k |
= 0, |
(2.33) |
∂t |
∂x |
|
|
где c(k) =Q′(k) = vв (k) + kvв′(k) – скорость распространения возму-
щений.
Соотношение q(k) = kvв(k) играет важную роль в теории транспортных потоков и называется фундаментальной диаграммой (рис. 2.2). В модели Лайт- хилла-Уизема эта зависимость непрерывна, следовательно, предельная пропускная способность участка дороги определяется плотностью потока.
Общий вид решения нелинейного уравнения (2.33)
q
qmax
0 |
k |
Рис. 2.2. Фундаментальная диаграмма транспортного потока
33
c(x,t) = F (x −vt), |
(2.34) |
где F – произвольная функция. Соотношение (2.34) описывает бегущую волну, рассматриваемую как волну уплотнения в среде. Волны типа (2.34) называют кинематическими волнами, что подчеркивает их кинематическое происхождение в противоположность динамической природе акустических и упругих волн.
Ударные волны в транспортном потоке
Зависимость скорости от интенсивности движения приводит к образованию ударной волны в транспортном потоке. Пусть скорость автомобилей в потоке лежит в пределах
0 < v < v0 , |
(2.35) |
так, что [(dq)/(dv)] > 0. Если по какой-либо причине скорость некоторой части потока понизится на ∆v, интенсивность движения понизится на kj(1– 2v/v0)∆v. Плотность этой части потока k повысится, и скорость будет далее снижаться. Возмущение скорости является незатухающим, что и демонстрирует неустойчивость поведения транспортного потока. В этих случаях автомобили в потоке вынуждены неоднократно трогаться с места и останавливаться. Это явление носит название ударной волны.
2.3. Микроскопические модели транспортного потока
Микроскопические модели представляют движение отдельных автомобилей. При значительных интенсивностях это движение ограничено впереди идущими автомобилями.
Модели следования за лидером
Первоначально предполагалось, что каждый водитель согласует свою скорость со скоростью впереди идущего автомобиля:
x(t) = |
1 |
(x |
(t) − x |
(t)), |
(2.36) |
|
τ |
i |
i+1 |
|
|
34

где τ – время согласования скоростей (рис. 2.3); точки над координа- 
 той обозначают дифференцирование
той обозначают дифференцирование 
по времени. |
|
i+1 |
i |
|
Рис. 2.3. Порядок следования |
||
Данная модель не |
описывает |
||
свойств неустойчивости, |
возникно- |
|
автомобилей |
|
|
||
вения ударных волн и заторов. В левую часть уравнения (2.36) можно добавить задержку td, описывающую время реакции водителя на изменение скорости лидирующего автомобиля. Множитель 1/τ в этом уравнении интерпретируется как коэффициент чувствительности α, характеризующий скорость реакции водителя. Тогда (2.36) можно записать в виде дифференциально-разностного уравнения
xi (t +td ) = α(xi (t) − xi+1 (t)). |
(2.37) |
При α = const условие неустойчивости уравнения (2.37) имеет вид td/τ > 1/2. Наличие неустойчивости позволяет моделировать ударные волны и заторы, но предположение о неизменности чувствительности не позволяет воспроизвести фундаментальную диаграмму. Более адекватная модель получается при учете возрастания чувствительности с уменьшением дистанции до лидирующего автомобиля. С этой точки зрения уравнение (2.37) может быть преобразовано к виду
xi+1 (t +td ) = α(xi+1 (t +td )) |
n1 |
x(t) − xi+1 (t) |
(2.38) |
|||
|
|
|
|
. |
||
|
(x |
(t) − x |
(t))n2 |
|||
|
|
i |
i+1 |
|
|
|
Оценка коэффициентов n1 и n2 проводится по экспериментальным данным. В простейшем случае, используемом для теоретического анализа, n1 = 0, n2 = 1.
xi+1 |
(t +td ) = α |
x |
(t) − xi+1 |
(t) |
. |
(2.39) |
|
xi (t) − xi+1 (t) |
|||||||
|
|
|
|
||||
После интегрирования уравнения (2.39) получаем
35
xi+1 (t +td ) = ln(kmax (xi (t) − xi+1 (t))), |
(2.40) |
где kmax – константа, описывающая движение автомобилей в плотном потоке на очень близком расстоянии «бампер-к-бамперу».
Когда транспортный поток является стационарным, плотность k выражается формулой k = 1/(xi(t) – xi+1(t)), а так как скорость в стационарном режиме постоянна, то
v = |
1 ln |
kmax |
. |
(2.41) |
|
||||
|
τ |
k |
|
|
Теория следования за лидером слишком детальна для ее использования при анализе движения в больших городских транспортных системах. Но эта теория является достаточным инструментом микроскопического моделирования транспортного потока, а также часто используется для анализа характеристик потока на различных пересечениях, перекрестках и т.д.
Клеточные автоматы
Клеточный автомат – это математическая модель, представляющая идеализированную физическую систему, в которой пространство и время дискретны, а множества значений физических величин конечны. В простейшем виде клеточные автоматы представляют собой двумерную сетку произвольного размера, состоящую из ячеек. Состояние сетки (конфигурация) обновляется с течением времени, причём состояние каждой ячейки в следующий момент времени зависит от состояния ближайших её соседей (смежных ячеек) и, возможно, от её собственного состояния на текущей итерации. Количество возможных состояний ячейки конечно. Обновление конфигурации происходит параллельно, в соответствии с определёнными для данной модели правилами.
При применении клеточного автомата для моделирования движения транспортного потока исследуемый участок дорожного пути формализуется в виде двумерной матрицы. Число строк матрицы равно числу полос движения моделируемого участка, а число столб-
36

цов определяется исходя из принятого масштаба клетки и общей протяжённости дороги (рис. 2.4). Как правило, масштаб выбирается таким образом, чтобы в клетку по длине вмещался точно один автомобиль с учётом безопасного расстояния до транспортных средств в соседних клетках. В любой момент времени каждая ячейка может быть либо пуста, либо занята транспортным средством.
Рис. 2.4. Многополюсный транспортный клеточный автомат
Время в модели дискретно, значение размера шага обновления принимается из диапазона от 0,6 до 1,2 секунд, что приблизительно соответствует времени реакции водителя на изменение дорожной ситуации. Позиция автомобиля однозначно определяется номером строки – принятой полосой движения – и номером столбца – текущей координатой на отрезке транспортного пути.
В ходе моделирования на каждом шаге эксперимента ко всем автомобилям параллельно и независимо применяются принятые в модели правила обновления состояний.
Например, для воспроизведения трафика однополосной магистрали при переходе к новому состоянию все транспортные средства параллельно и независимо друг от друга обновляют значения скорости и координаты в соответствии с последовательным выполнением следующих шагов (правил):
1. Ускорение. Если скорость i-го транспортного средства меньше предельного значения vi(t) < vmax и расстояние до следующего впереди автомобиля ∆xi(t) больше vi(t) + 1: ∆xi(t) > vi∆t + 1, то скорость следует увеличить на единицу:
i ( |
) |
i ( |
) |
+1. |
|
v |
t +1 |
= v t |
|
(2.42) |
|
|
|
|
|
|
37 |
2. Торможение. Если ∆xi(t) ≤ vi∆t + 1, тогда новое значение скорости
i ( |
) |
i |
|
v |
t +1 |
= ∆x / ∆t −1. |
(2.43) |
3. Случайные воздействия. С заданной вероятностью скорость транспортного средства уменьшается на единицу:
i ( |
) |
i ( |
) |
−1 |
|
v |
t +1 |
= v t |
|
(2.44) |
при условии, что текущее значение положительно (vi(t) > 0).
4. Передвижение. Транспортное средство перемещается вперёд на vi (t +1) ячеек:
i ( |
) |
i ( |
) |
i ( |
) |
∆t. |
|
x |
t +1 |
= x t |
|
+v |
t +1 |
(2.45) |
Естественное желание водителей двигаться быстрее, не превышая максимально возможное на данном участке дороги значение скорости, формализует правило 1. Правило 2, торможение, обеспечивает отсутствие столкновений при превышении скорости. Правило 3 определяет стохастический характер модели: отсутствие вероятности делало бы моделирование полностью детерминированным – точно предсказуемым на любом шаге при известных начальных значениях переменных, – что недопустимо при воспроизведении динамики реального транспортного движения.
Достоинство модели клеточных автоматов состоит в отсутствии сгустков и заторов, автомобили продолжают движение на минимальных скоростях и при большой плотности.
Применение клеточных автоматов в моделировании дорожного движения является перспективным направлением, характеризуемым высокой вычислительной скоростью и эффективностью. Этот подход может быть классифицирован как имитационный и позволяет представлять динамику системы во времени. Кроме того, разделение машин по типам в этом случае является простой задачей, что отличает его от аналитических моделей. Однако у этих моделей есть некоторые недостатки: исключаются резкие изменения параметров движения при малых плотностях потока; из-за последовательного обновле-
38
ния заторы становятся неустойчивыми; скорость автомобилей не согласуется с реальными данными, особенно в режимах пробок.
Вопросы для самоконтроля
1.Назовите объекты микро- и макроскопического моделирования транспортных средств.
2.Что характеризуют основные параметры: интенсивность, состав и плотность транспортного потока?
3.Как подразделяют транспортные потоки по степени стеснен-
ности?
4.От чего зависит максимальная конструктивная скорость автомобиля?
5.Как связаны в пределах некоторого диапазона скорость, интенсивность и плотность транспортного потока?
6.Как связаны пространственная и временная плотности распределения скоростей?
7.Закон сохранения транспортного потока.
8.Аппроксимация зависимости скорости транспортного потока от его плотности по Гриншилдсу.
9.Зависимость скорости транспортного потока от его плотности по Гринбергу.
10.Фундаментальная диаграмма транспортного потока, модель Лайтхилла-Уизема.
11.Микроскопические модели: модель следования за лидером.
12.Микроскопические модели: модель клеточных автоматов.
39
3. ДВИЖЕНИЕ ТРАНСПОРТНЫХ СРЕДСТВ НА ПЕРЕКРЕСТКАХ
3.1. Типы перекрестков. Анализ конфликтных точек
Перекрестком называется место пересечения или примыкания улиц или дорог. В зависимости от формы различают следующие типы перекрестков:
•крестообразный четырехсторонний – одна улица пересекает другую под прямым углом или под углом, близким к прямому;
•Х-образный четырехсторонний – одна улица пересекает другую не под прямым углом;
•четырехсторонний смешанный – одна из улиц не имеет прямого продолжения, причем образуется как бы два трехсторонних перекрестка;
•Т-образный трехсторонний – одна улица примыкает к другой под прямым углом или близким к прямому;
•У-образный трехсторонний – две улицы сливаются в одну под острым углом;
•многосторонний – улицу пересекает бульвар самостоятельными проездами с обеих сторон (обычно с односторонним движением) или к перекрестку примыкает больше четырех проездов;
•площадью называется перекресток различной конфигурации,
ккоторому обычно примыкают более четырех проездов и который выходит за габариты образующих ее улиц.
Помимо планировочных условий перекрестки различаются по другим признакам: по способу регулирования движения (регулируемый или не регулируемый), по степени сложности (с пересечением трамвайных путей, с поворотом трамвая и т.п.).
Согласно действующим техническим условиям регулирование движения на перекрестках вводится, когда сумма потоков, притекающих со всех направлений к перекрестку, составляет не менее 800 транспортных единиц в 1 ч, а суммарная интенсивность пешеходного движения – не менее 600 чел/ч.
40
