Математические модели движения транспортных средств

Вероятность того, что абсолютное отклонение будет меньше утроенного среднеквадратичного отклонения, равна 0,9973, и большие отклонения практически невозможны. В этом состоит «правило трех сигм»: при нормальном распределении случайной величины абсолютная величина ее отклонения от математического ожидания не превышает утроенного среднего квадратичного отклонения.

Это правило применяют для проверки нормальности распределения изучаемой величины и для выявления грубых ошибок (промахов) в экспериментальных данных.

Пример 7.6. При измерении скорости автомобилей на участке дороги установлено, что скорость (случайная величина x) распределена нормально со средним квадратичным отклонением 20 км/ч. Необходимо найти вероятность доли автомобилей, превышающих максимально допустимую скорость на 20 км/ч.

Решение. Используем формулу (7.32). По условию задачи ε = = 20 км/ч, σx = 10 км/ч, следовательно, вероятность доли автомобилей, соблюдающих скоростной режим,

p(∆X ≤ 20) = 2Ф(21) = 2Ф(2) = 0,9544.

Вероятность доли автомобилей, превышающих максимально допустимую скорость на 20 км/ч, равна вероятности противоположного события:

p(∆X ≥ 2) =1−0,9544 ≈ 0,05.

7.4.2. Экспоненциальное распределение

Экспоненциальное распределение применяется для описания частости автомобилей, проходящих через сечение дороги, а также частости интервалов между автомобилями. Такое распределение характерно для внезапных отказов элементов и систем автомобиля. Плотность вероятности экспоненциального распределения задается уравнением

где λ − параметр распределения, являющийся строго положительной константой.

Среднее значение x и среднеквадратическое отклонение σ экспоненциального распределения совпадают и равны обратному значению параметра x = σ = 1/λ. Графики функций F(х) и f(x) приведены на рис. 7.12.

Рис. 7.12. Графики плотности f(x), интенсивности отказов λ(x) (а) и функции F(x) экспоненциального распределения (б)

Основное свойство экспоненциального закона состоит в том, что при нем вероятность безотказной работы на данном интервале не зависит от времени предшествующей работы, а зависит от длины интервала. Это значит, что будущее поведение автомобиля не зависит от прошлого, если в данный момент он исправен.

7.5.Представление распределения скоростей автомобилей

втранспортном потоке

При моделировании потоков используют законы распределения их параметров. Фактические данные о распределениях параметров транспортных потоков на магистрали можно получить лишь экспериментальным путем.

Рассмотрим экспериментальное измерение распределения скоростей автомобилей в транспортном потоке и обработку получаемых результатов.

132

Методика измерения

Для измерения скоростей автотранспортных средств обычно применяют радары. Они позволяют замерить скорость одиночного автомобиля и автомобиля, движущегося в группе. Погрешность измерения скорости радаром не превышает 1 км/ч. Скорость можно измерять на расстоянии до 300 м. Наименьшее значение скорости обычно ограничено величиной 20 км/ч, наибольшее значение составляет 200 км/ч.

При измерении используют метод стационарных наблюдений. Этим методом также пользуются при измерении пространственных и временных интервалов между автомобилями. В контрольном сечении дороги с равномерным потоком проводят замеры, при этом обеспечивают большое число замеров и их случайный порядок. В сводку наблюдений вносят номера автомобилей, скорости движения и диапазоны скоростей, в которых располагаются скорости автомобилей.

Обработка результатов измерений

Фактический диапазон скоростей автомобилей разбивают на интервалы. Затем находят частоту n – число автомобилей, скорость которых располагается в каждом интервале. Сумма частот должна быть равна числу автомобилей. Находят частости, равные отношениям частоты к числу автомобилей. Частость соответствует вероятности события, заключающегося в том, что скорость автомобиля располагается в заданном интервале. Сумма частостей должна быть равна единице.

Находят накопленную частость на заданных интервалах, которая равна числу автомобилей (в %), скорость которых меньше средней скорости интервала. Для диапазона, соответствующего максимальной скорости, накопленная частость равна 1.

В табл. 7.1 представлены результаты обработки наблюдений для 100 автомобилей с 8 интервалами скоростей их движения.

Результаты представляют в виде гистограмм. Для построения графиков вычисляют среднее значение скорости vc на интервалах.

133

Они указаны в последнем столбце табл. 7.1. Примеры построения гистограмм показаны на рис. 7.13–7.15. По гистограммам легко видеть, что 36 % автомобилей превышают скорость 60 км/ч.

Рис. 7.13. Гистограмма распределения частоты скоростей автомобилей

134

Рис. 7.14. Гистограмма распределения частости скоростей

Рис. 7.15. Гистограмма распределения накопленной частости

Рис. 7.16. График изменения частости скоростей

135

Гистограммы также представляют в виде графиков. Для этого используют средние значения скоростей vc на интервалах (см. табл. 7.1). Значения частостей отражают на графике точками (рис. 7.16). Точки соединяют прямыми линиями.

7.6. Основы корреляционного и регрессионного анализа

Целью моделирования любого процесса является установление количественной зависимости выходного параметра от одного или группы случайных входных параметров. Например, выбор водителем скорости движения транспортного средства зависит от многих факторов: вида транспортного средства, состояния дорожного покрытия, числа полос, самочувствия самого водителя и других факторов. В функциональной связи Y = f (X) каждому значению независимой переменной X отвечает одно или несколько вполне определенных значений зависимой переменной Y. В этом случае связь между переменными X и Y в отличие от функциональной приобретает статистический характер и называется корреляционной.

Простейшей и распространенной зависимостью между величинами X и Y является линейная регрессия. Оценка тесноты или силы связи между величинами X и Y осуществляется методами корреляционного анализа.

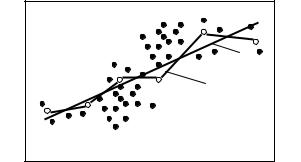
Рассмотрим линейную регрессию от одного параметра (рис. 7.17). Пусть для произвольного фиксированного значения x получено несколько значений y. Предполагается, что величина Y распределена нормально с математическим ожиданием

и дисперсией σ2y , не зависящей от X.

Из (7.35) видно, что случайная величина Y в среднем линейно зависит от фиксированного значения x, а параметры b0 , b1 и σ2y являются неизвестными параметрами генеральной совокупности.

136

Пример 7.9. Построить линейную зависимость регрессии по семи экспериментальным точкам:

Решение

По формуле (7.42) получаем искомую зависимость

y= y +β1 (x − x ) = 2,764 +0,157(x −4).

7.6.2.Выборочный коэффициент корреляции

Коэффициент корреляции является количественной мерой, учитывающей стохастическую долю колебаний yi относительно средней y под влиянием xi.

Выборочный коэффициент корреляции вычисляют по формуле

n

∑(xi − x )( yi − y )

где σx и σy – выборочные средние квадратичные отклонения,

139

Коэффициент корреляции не может быть использован для оценки технологической важности фактора. Его величина указывает только на тесноту связи между переменными, а знак – на характер влияния. Значения коэффициента корреляции находятся в пределах

−1 ≤ r ≤1:

при r < 0 – увеличение x вызывает уменьшение y; при r > 0 – увеличение x вызывает увеличение y;

при r =1 – связь между x и y линейная функциональная;

при r = 0 – корреляционной связи между x и y нет или она не-

линейная.

Если выражение (7.44) преобразовать к виду

Отсюда видна непосредственная связь коэффициента корреляции r и коэффициента β1 в уравнении линейной регрессии, их знаки всегда совпадают.

Выражения (7.44), (7.45) выражают тесноту и вид связи между переменными x и y.

140