1.10.2. Процесс случайного блуждания и единичный корень

При анализе временных рядов важно знать, является ли ряд стационарным. Рассмотрим стационарный AR(1)-процесс или процесс Маркова: y_t = β₁y_t-1 + u_t с , N(0, ). Используя лаговый оператор, перепишем преобразованное выражение y_t – β₁y_t-1 = u_t в виде (1 – β₁L)y_t-1 = u_t. Откуда видим, что корень лагового оператора (т.е. корень уравнения =0) равен 1/ , который при условии больше единицы. Как мы видели, процесс случайного блуждания (он не стационарный) имеет единичный корень, а стационарный AR(1) процесс – корень, который меньше единицы. Поэтому, чтобы протестировать временной ряд на стационарность, достаточно рассмотреть нулевую гипотезу против альтернативной гипотезы H₁: .

Итак, одним из методов тестирования временного ряда на стационарность является проверка гипотезы о единичном корне в уравнении _t = ₁y_t-1. Как известно, осуществить эту проверку можно на основании t-статистики. Однако, как показали Дики и Фуллер (D.A. Dickey, W.A. Fuller), если верна нулевая гипотеза о единичном корне, то в этом случае t-статистика не следует распределению Стьюдента (дисперсия процесса зависит от времени). Фуллер построил таблицу для определения критических значений t-статистики для случая единичного корня, отсюда название этой t-статистики (DF-t-статистика) и теста (Dickey–Fuller Unit Root Test).

Чтобы было удобнее тестировать гипотезу о единичном корне, исходное уравнение теста y_t = β₁y_t-1 + u_t преобразовывается к виду Δy_t = (β₁ – 1)y_t-1 + u_t или, после замены к виду Δy_t = y_t-1 + u_t. Тогда нулевая гипотеза формулируется в привычном для такой проверки виде: (в этом случае β₁ = 1), а альтернативная гипотеза формулируется в виде (т.е. β₁ < 1). Поскольку вариант β₁ > 1 не рассматривается (взрывной процесс), то в этом случае формулируется односторонняя гипотеза. Тестируется на основе DF-t-статистики, которая, если верна , имеет DF-t-распределение. Критические значения этой статистики зависят от вида тестируемой модели, а именно: включены ли в модель константа или константа и детерминированный тренд. Эта информация будет нужна при заполнении диалогового окна теста Дики – Фуллера. Соответствующий запрос появится при вызове процедуры этого теста в пакете EViews (рисунок 1.24).

Рисунок 1.24 – Диалоговое окно теста Дики – Фуллера на единичный корень

Как видим, в позиции «Include in test equation – включить в тестовое уравнение» предполагается три варианта – включить в тестовое уравнение пересечение (константу), тренд и пересечение и ни того ни другого (None). На рисунке 1.24 выбрана процедура включения в модель константы (Intercept). В позиции «Test for unit root in – тест на единичный корень в» предлагается также три варианта модели: в уровнях временного ряда, в первых разностях и во вторых разностях (на рисунке 1.24 выбрано «в уровнях» «Level»). Кроме того, в позиции «Automatic selection – выбор автоматически» проставлен информационный критерий Шварца и указано максимальное число лагов – 13. По указанному критерию в автоматическом режиме выбирается оптимальное число лаговых значений анализируемого ряда.

Дело в том, что DF-тест используется только для AR(1)-процессов, т.е. остатки в тестируемой модели не должны быть автокоррелированными (в противном случае тест некорректен). В общем случае, чтобы избавиться от автокорреляции в остатках тестового уравнения, в рассматриваемый тест включаются слагаемые приращений остатков более высокого порядка (Δu_t-j). При этом оптимальный лаг для таких приращений, т.е. величина лага j, по умолчанию подбирается на основе информационного критерия Шварца (возможно также использование и других критериев, например Акаике). Известно, что включение в тестовое уравнение лаговых значений остатков не влияет на критические значения ADF-t-статистики. Такой тест называется расширенным тестом Дики – Фуллера (Augmented Dickey-Fuller test или ADF-тест) (см. рисунок 1.24 в позиции «Test type»).

Для иллюстрации работы теста приведём результаты тестирования рядов, рассмотренных ранее (графики этих рядов показаны на рисунке 1.22). Как мы видели, оба эти ряда были стационарными, что и подтвердил анализируемый тест (рисунок 1.25). В обоих случаях вероятности для t-статистики равны нулю, что отклоняет гипотезу о единичном корне.

Далее в отчёте приведены критические значения t-статистики (Test critical values) для разных уровней значимости (1-, 5-, и 10%). Все они правее вычисленных значений (в одном случае – это (–10,98) для примера белого шума, в другом – (–6,814)), т.е. расчётные значения t-статистик попали в критическую область.

Как отмечалось, здесь проверяется односторонняя гипотеза, т.е. альтернативная гипотеза формулируется как . Таким образом, в обоих случаях имеем стационарные временные ряды. Обратите внимание на то, что в случае белого шума (левая часть рисунка 1.25) гипотеза о единичном корне отклоняется более уверенно (расчётное значение t-статистики по абсолютной величине больше, чем в правой части рисунка).

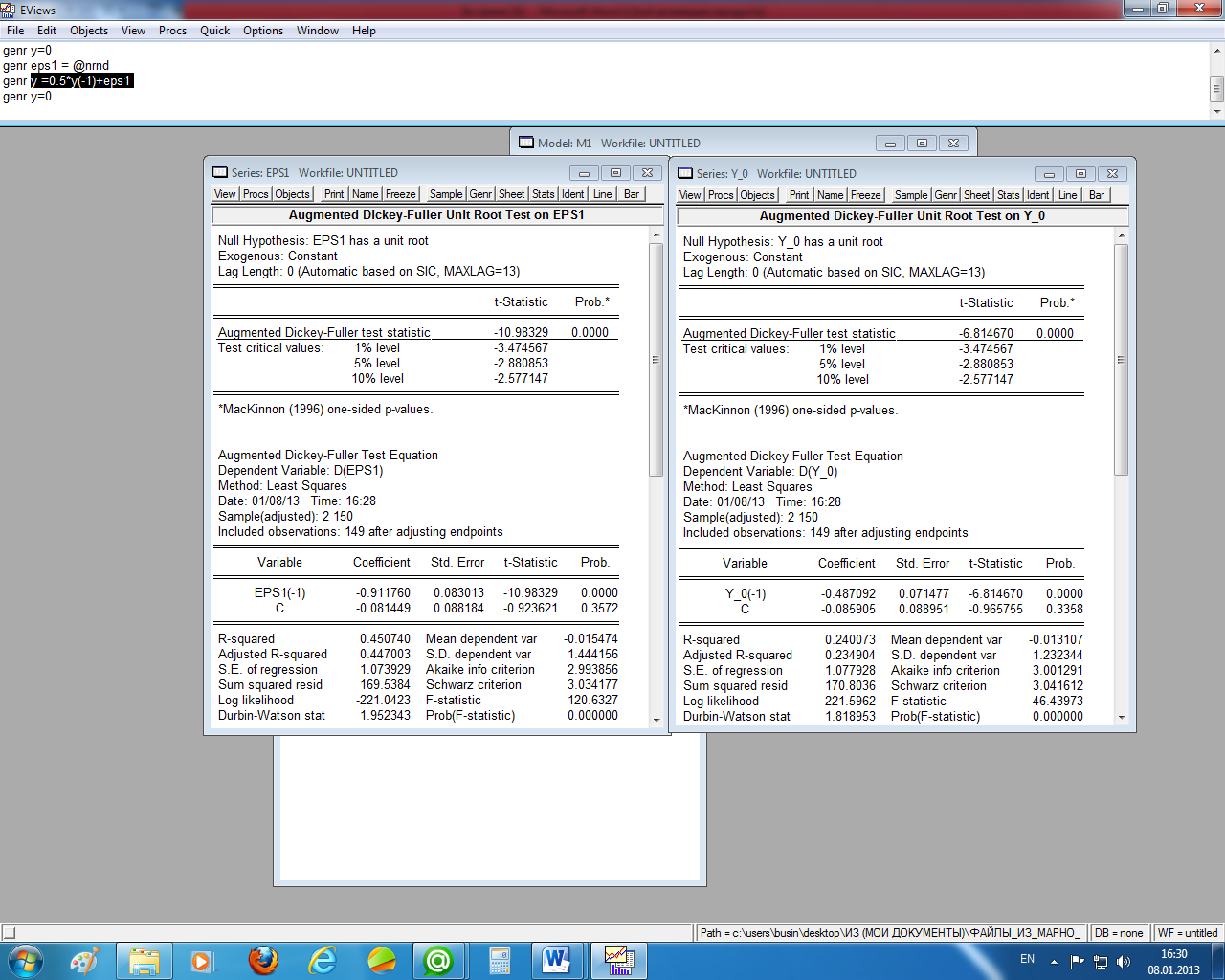
Рисунок 1.25 – Тесты Дики – Фуллера для анализируемых рядов

В нижней части рисунка приведены уравнения теста. Лаговые значения разностей в них не вошли. Например, для правого рисунка тестовое уравнение имеет вид Δ(Y_0)_t = С + (Y_0)_t-1 + u_t, что и отражено в нижней части рисунка.