1.7. Применение фиктивных переменных при моделировании тренда

Воспользуемся идеей американского экономиста Д. Гуйарати и промоделируем динамику этого ряда, включив в модель регрессии фиктивные переменные. Одна из них (d₁) будет отвечать за изменение константы при переходе от одного периода к другому, а вторая (d₂) – за изменение угла наклона линии тренда. Переменная d₁ принимает значение 1 для t < n₁ и 0 для остального периода. Переменная d₂ = d₁ t и, соответственно, будет менять угол наклона тренда после периода t = n₁. Уравне6ие тренда в этом случае примет вид

lnGDP_t = a + b d₁+c t + f d₂ +e_t.

В этом случае до периода n₁ переменная d₁ = 0 и уравнение тренда примет вид

lnGDP_t = a +c t +e_t,

а после этого периода уравнение тренда примет вид

lnGDP_t = (a + b)+(c + f) t +e_t.

Таким образом, после периода t = n₁ может поменяться и свободный член, и угол наклона тренда. Проиллюстрируем это на нашем примере. Введём переменные d₁ и d₂ и введём в окно спецификации регрессии выражение

logGDP @trend d₁ d₂ c.

Получим

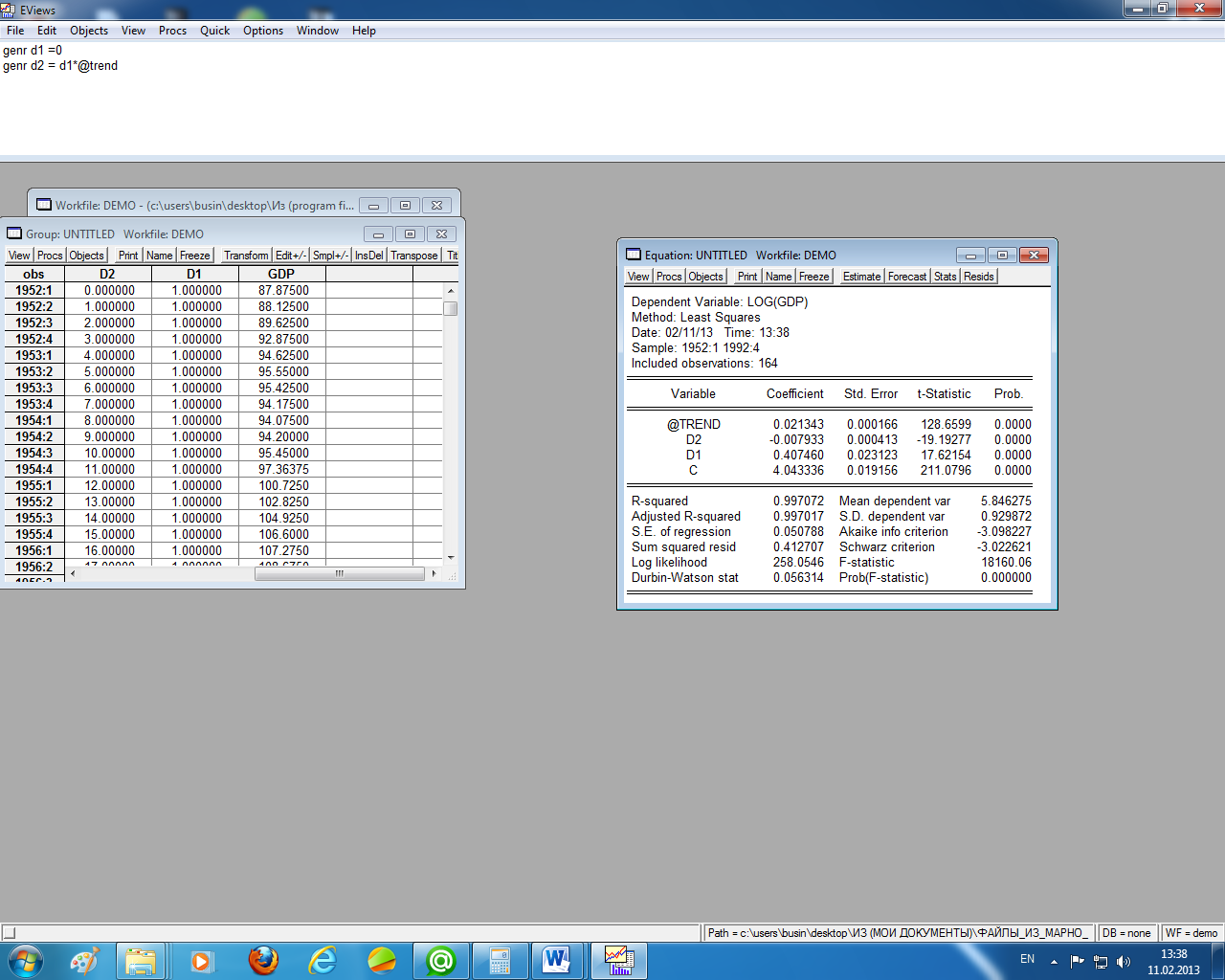
Рисунок 1.13 – Уравнение тренда с фиктивными переменными

Все оценки параметров этого уравнения значимы, следовательно, действительно после периода t = n₁ произошли значимые изменения в динамике ряда по сравнению с линейным трендом.

Сравнивая два полученных уравнения тренда (рисунки 1.10 и 1.13), видим, что последнее уравнение предпочтительнее: и более точное и с меньшей ошибкой. Да и графики остатков этих трендов (рисунки 1.11 и 1.14) «говорят» в пользу последнего уравнения.

Таким образом, до 1967 года уравнение тренда будет иметь вид

lnGDP_t = 4,04 + 0,02*t + e_t,

а после 1967 года

lnGDP_t = 4,45 + 0,013*t +e_t.

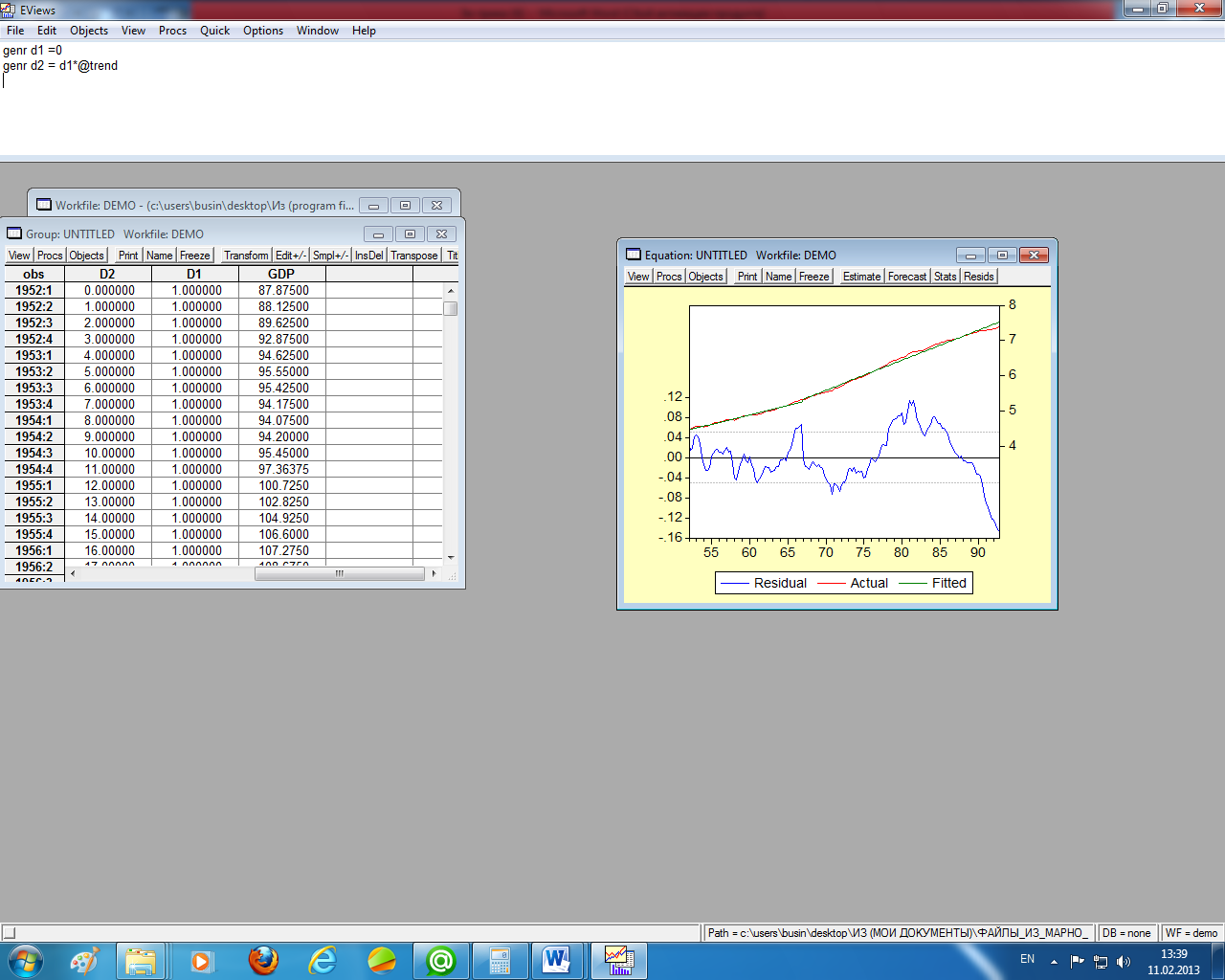
Рисунок 1.14 – Графики уравнения тренда и остатков

Этот метод можно использовать не только в дополнение к тесту Чоу, но и самостоятельно для проверки гипотезы о структурной стабильности тенденции изучаемого временного ряда. Основное его преимущество перед тестом Чоу состоит в том, что нужно построить только одно, а не три уравнения тренда.

Отметим в заключение, что тест Чоу, а также модель с фиктивными переменными, может использоваться при проверке гипотез о структурной стабильности и в более сложных моделях взаимосвязи двух и более временных рядов.

1.8. Сезонная декомпозиция временного ряда

Это один из наиболее простых методов анализа временных рядов и прогнозирования на их основе будущих значений изучаемого процесса, если считать, что на формирование значений показателей временного ряда оказывают влияние три выше рассмотренных фактора – случайная, трендовая и сезонная компоненты. От случайной компоненты обычно избавляются путём усреднения, трендовую компоненту можно выделить, например, используя МНК, как в предыдущем пункте, а случайная компонента нужна для проверки адекватности модели, о чём речь ниже.

Для прогнозирования временного ряда, включающего все три компоненты, необходимо определить, каким образом они сочетаются при формировании значений элементов временного ряда – мультипликативно или аддитивно.

Считается, что если вклад сезонной компоненты остаётся на постоянном уровне для всего рассматриваемого периода времени, то желательно использовать аддитивное представление, а если по мере движения по времени амплитуда сезонной компоненты изменяется, то рекомендуется использовать мультипликативную модель временного ряда, хотя возможны и другие критерии.

В моделях с аддитивным и с мультипликативным представлением компонент элементов временного ряда общая процедура анализа в принципе одинакова. Обычно она состоит в установлении и исключении воздействия на величину элементов временного ряда каждой компоненты по отдельности. Этот процесс называется разложением или сезонной декомпозицией временного ряда.

Рассмотрим кратко эту процедуру для мультипликативной модели.

На первом шаге избавляемся от сезонной компоненты на основе усреднения простыми скользящими средними. Причём интервал усреднения берётся равным длине сезонности. Поскольку длина сезонности, как правило, величина чётная (4 – если поквартальные данные и 12 – если помесячные), то усреднение проводится на основе вычисления хронологической или центрированной скользящей средней.

В результате получаем трендовую составляющую (T_t) в виде совокупности точек. Разделив исходные данные на трендовую компоненту, получим сезонно-случайную компоненту (если исходная модель имеет вид: y_t = T_t S_t I_t, то получаем – y_t/T_t = S_t I_t).

Усреднив случайную компоненту (вычисляя среднюю арифметическую уровней элементов полученного ряда по соответствующим периодам), получим в чистом виде сезонную компоненту или индекс сезонности (S_t). Он показывает, во сколько раз в среднем уровни ряда в соответствующем сезоне отличаются от аналогичных уровней по полученному в предыдущем шаге тренду.

Вычислив индекс сезонности, делим на него уровни исходного ряда и получаем данные, исправленные на сезонность (y_t/S_t) = T_t I_t.

И уже по этим данным путём аналитического выравнивания методом наименьших квадратов подбираем адекватную модель тренда как функцию от времени (T_t =f(t)).

Прогноз по этому методу осуществляется на основе тренда с поправкой на сезонность (f_t = T_t S_t).

Для аддитивной модели все рассмотренные процедуры аналогичны, только вместо деления надо брать вычитание, а вместо умножения – суммирование.

Рассмотрим реализацию этого метода на примере мультипликативного представления модели временного ряда. Пусть имеются данные, показывающие продажу учебников (в тыс. шт.) за последние три года поквартально (таблица 1.1).

Таблица 1.1 – Поквартальные данные продажи учебников

Год		1				2				3
Квартал	1	2	3	4	1	2	3	4	1	2	3	4
Продажа	16,9	9,4	26,2	25	18	9	29	23,6	18,5	11	29,2	26,2

Анализ начнём с геометрического представления исходных данных.

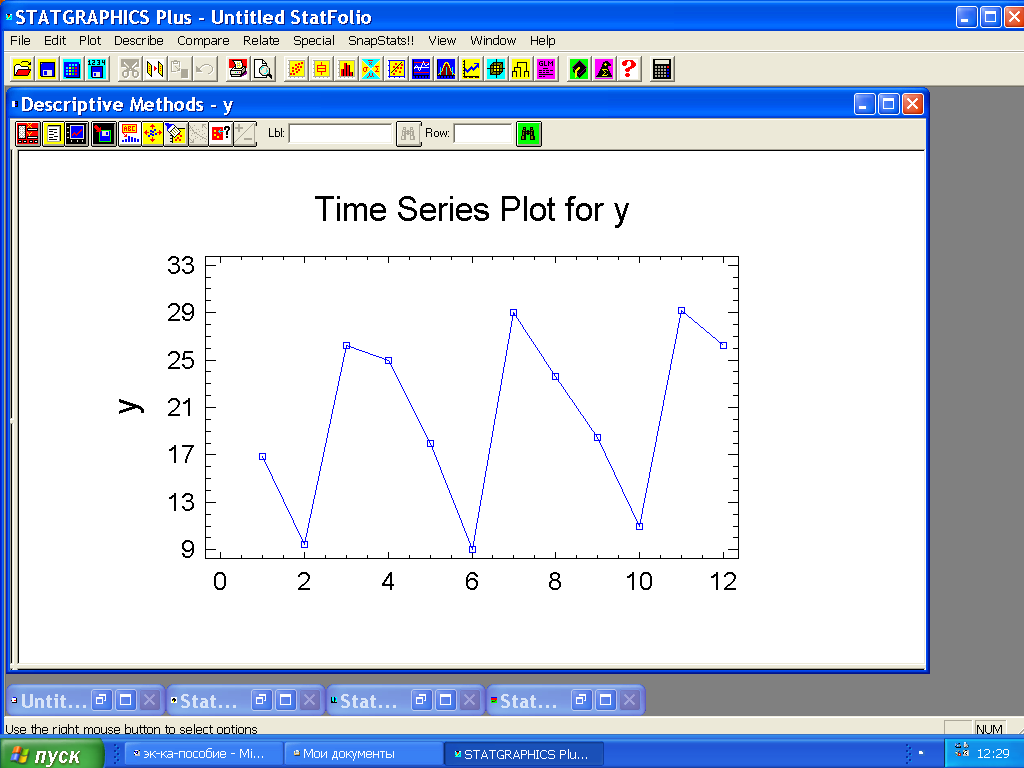
Рисунок 1.15 – Горизонтальный график ряда продажи учебников

Как видим (рисунок 1.15), в приведенных данных отчётливо прослеживается сезонная компонента, поэтому прогнозирование уровня продаж на очередной год проведём методом сезонной декомпозиции.

Все вычисления приведены на рисунке 1.16, где указаны: номера исходных данных (Period), сами исходные данные (Data), центрированная скользящая средняя или трендово-циклическая компонента (Trend-cycle), сезонно-случайная компонента (Seasonality), случайная компонента (Irregular), а также ряд с устранённой сезонностью (Seasonally Adjusted).

Р 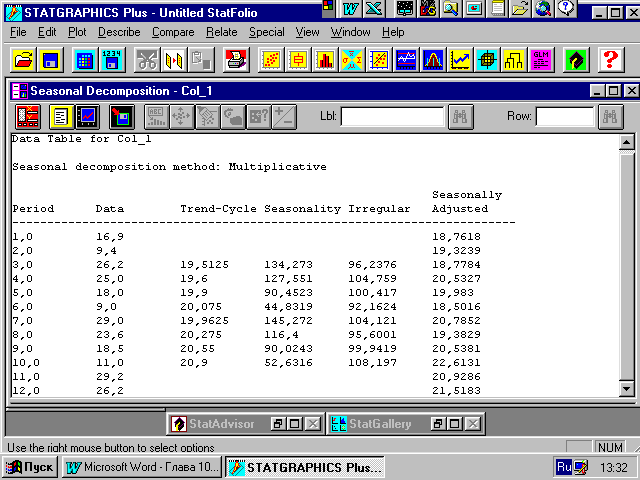исунок 1.16 – Окно отчёта ППП Statgraphics о реализации метода сезонной декомпозиции

Усреднив сезонно-случайную компоненту по соответствующим кварталам, получим индекс сезонности (в процентах):

90,1 48,6 139,5 121,8

Графически индекс сезонности представлен на рисунке 1.17.

Как видим, уровни продаж в первые два квартала ниже среднего уровня (в I кв. на 9,9 %, во II – на 51,4 %), а в последние два квартала – выше (соответственно на 39,5 % и на 21,8 %).

Рисунок 1.17 – График сезонной компоненты

Если для мультипликативного представления временного ряда сезонная компонента представляет собой индекс сезонности, указывающий, во сколько раз уровень продаж выше или ниже среднего, определяемого на основе тренда, то для аддитивного – абсолютную величину превышения или занижения продаж по отношению к их среднему уровню.

Кроме того, при правильных расчётах сумма индексов сезонности должна быть равна длине сезонности в случае мультипликативного представления (у нас – 400, т. к. индекс выражен в процентах) и должна быть равна нулю – при аддитивном представлении.

На рисунке 1.18 приведён график данных, исправленных на сезонность. Как видим, после устранения сезонной компоненты чётко прослеживается трендовая составляющая, отражающая растущие продажи во времени по линейному тренду.

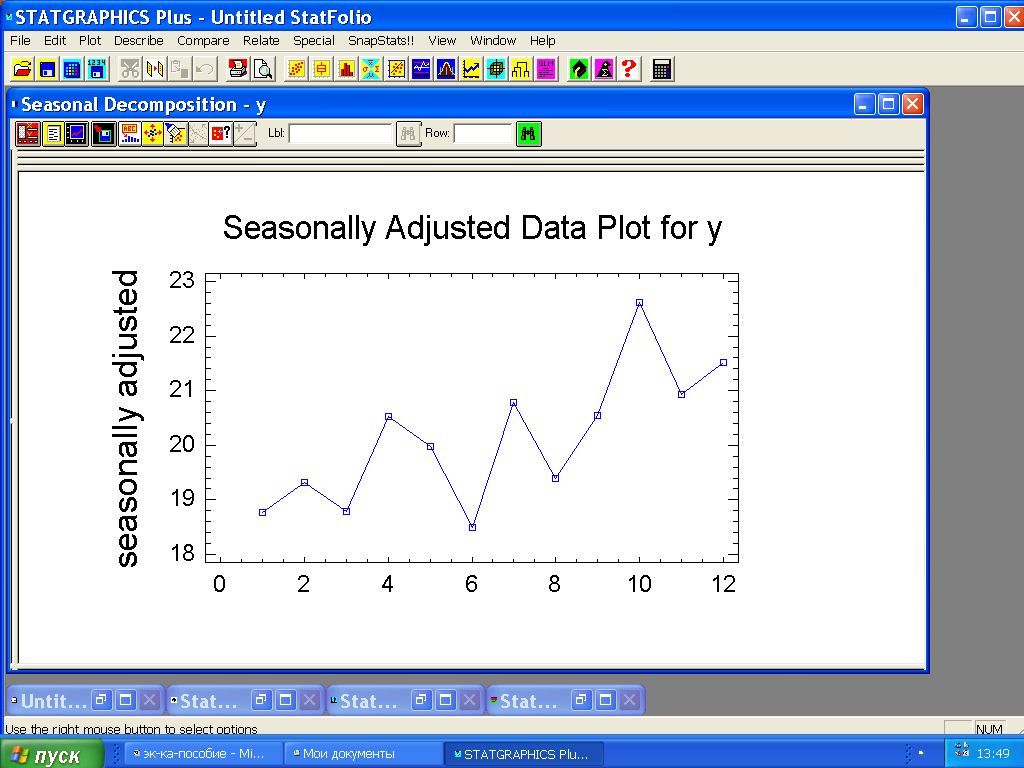
Рисунок 1.18 – График ряда с устраненной сезонной компонентой

В нашем случае уравнение линейного тренда имеет вид:

T_t = 18,5 + 0,25t.

Прогнозные значения по тренду с учётом сезонной компоненты приведены в таблице 1.2.

Таблица 1.2 – Расчет прогноза с учетом сезонной компоненты

Год	Квартал	Прогноз по тренду	Индекс сезонности	Квартальный прогноз на очередной год
4	1 2 3 4	21,78 22,03 22,28 22,53	0,906 0,486 1,395 1,218	(21,78)(0,909) = 19,80 (22,03)(0,486) = 10,71 (22,28)(1,395) = 31,08 (22,53)(1,218) = 27,44