1.3. Показатели точности прогноза

Любой прогноз несёт на себе определённую степень ошибки, поэтому при проведении прогнозов на основе той или иной модели исследователь всегда имеет дело со случайными отклонениями прогнозных значений от их реальных текущих и будущих значений. Такие отклонения в случае правильной спецификации модели предполагаются распределёнными нормально, а мерой их рассеяния вокруг прогнозных значений служат различные показатели точности прогноза.

Рассмотрим некоторые из них. Пусть y_t – реальные значения показателей временного ряда, а f_t – прогнозные. Тогда ошибка прогноза в период времени t составит:

e_t = y_t – f_t .

Средняя ошибка прогноза (МЕ) определится из соотношения

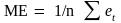
и характеризует степень смещённости прогноза. В идеальном случае МЕ  0. Если прогнозные значения в среднем завышены, то МЕ < 0, а если занижены, то МЕ > 0.

Средний квадрат ошибки прогноза (MSE) определяется из соотношения

.

Средняя абсолютная ошибка (МАЕ) вычисляется из соотношения:

.

MSE и МАЕ используются для сравнения процедур прогноза и подбора параметров сглаживания уровней элементов временного ряда.

Средняя абсолютная процентная ошибка (МРАЕ) вычисляется из соотношения:

и используется для оценки качества прогноза.

Если МРАЕ < 10%, то считается, что точность прогноза высокая, при 10% < МРАЕ < 20% – хорошая, если 20% < МРАЕ < 50%, то точность прогноза удовлетворительная и при МРАЕ > 50% – неудовлетворительная. МРАЕ вычисляется по ошибке прогноза на шаг вперёд.

Средняя процентная ошибка (МРЕ) вычисляется из соотношения:

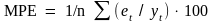
и служит показателем смещённости прогноза (не должна превышать 5%).

Кроме того, в некоторых статистических пакетах прикладных программ корень квадратный из MSE называется стандартной ошибкой и обозначается RMSE.

Из разработанных и используемых в практике методов анализа временных рядов рассмотрим лишь несколько наиболее простых, часто используемых на практике и теоретически обоснованных.

1.4. Сглаживание уровней временных рядов

Этот метод анализа применяется в основном для выявления основной тенденции в развитии исследуемого явления и предназначен для устранения высокочастотных колебаний в уровнях временного ряда. Хотя с помощью этого метода можно устранить и сезонные колебания, выбрав в качестве интервала усреднения длину сезонности.

Среди множества различных вариантов этого метода наиболее простым является вычисление простой скользящей средней. При этом сначала выбирается длина интервала сглаживания и вычисленное значение средней арифметической на этом интервале в начале ряда присваивается его середине. Затем это действие сдвигается по уровням ряда на один элемент вправо и расчёты повторяются, т.е. вычисление средней арифметической как бы скользит по уровням ряда. Отсюда и название метода.

Данный метод наиболее эффективен при линейной динамике уровней ряда. В более общем случае используются методы взвешенной скользящей средней. Наиболее часто из них применяется метод экспоненциально взвешенной скользящей средней. В этом методе учитывается старение информации при удалении её от текущего момента времени.

Рассмотрим простую экспоненциально взвешенную среднюю. Пусть прогнозное значение для периода t рассчитывается по формуле

f_t = 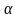y_t + (1 - )y_t-1 + (1 - )² y_t-2 +…+ (1 - )ⁿ y_{t- n} + … ,

где – показатель, характеризующий вес текущего наблюдения, называемый параметром сглаживания (0 < < 1).

Теоретически здесь предполагается бесконечный временной ряд с коэффициентами при лаговых значениях уровней временного ряда, убывающих по экспоненте. В силу того, что 0 < < 1, коэффициенты-веса при соответствующих элементах временного ряда быстро убывают, и достаточно несколько первых слагаемых этой суммы, чтобы получить результат с достаточной точностью.

Преобразуем это выражение. Вынесем за скобку (1 - ):

f_t = y_t + (1 - )[ y_t-1 + (1 - )y_t-2 +…+ (1 - )^n-1 y_t-n + …].

В квадратных скобках получили значение для f_t-1. Тогда можем записать:

f_t = y_t + (1 - )f_t-1. (1.1)

Тем самым мы получили модель экспоненциально взвешенной скользящей средней. Из (1.1) следует, что для того, чтобы вычислить экспоненциально взвешенную скользящую среднюю нет необходимости вычислять сумму длинного числового ряда, необходимо знать только значение уровня временного ряда в текущем периоде и экспоненциально взвешенную скользящую среднюю за предыдущий период.

Отметим, что сумма весов в выражении экспоненциально взвешенной средней (как сумма бесконечно убывающей геометрической прогрессии) равна единице.

Параметр сглаживания обычно подбирается по минимальной ошибке прогноза. С этой целью перебираются возможные значения и для каждого из них рассчитываются экспоненциально взвешенные средние и для нихт – ошибка прогноза, например, MSE. Минимальная ошибка и определит константу сглаживания. При расчётах на ЭВМ особых проблем при подборе не возникает ввиду автоматизации таких расчётов. Возможен и ручной вариант подбора значения этой константы.

После простого преобразования модели (1.1) экспоненциально взвешенные скользящие средние могут быть представлены в виде

f_t = f_t-1+ (y_t - f_t-1).

Данная форма представления модели оправдывает её название как адаптивной модели прогнозирования. По этой модели прогноз на очередной период t+1 равен предыдущему прогнозу плюс доля ошибки предыдущего прогноза, т.е. в модели учитываются результаты предыдущих прогнозов, т.е. прогноз на очередной период как бы адаптируется к результатам предыдущих прогнозов.

Есть разные рекомендации по выбору возможных значений , основная из них заключается в том, что при анализе стационарных временных рядов параметр сглаживания не должен выходить за пределы интервала 0,05 – 0,3. Считается, что если ошибка прогноза уменьшается при выходе значения за пределы указанного интервала, то это означает, что речь идёт о не стационарном временном ряде.

Следует отметить, что, как следует из (1.1), прогнозные значения при увеличении более динамичны и в большей мере отражают динамику исходных данных и, наоборот, чем меньше , тем прогнозные значения более сглажены. Поэтому, когда по ходу решения задачи требуется повысить чувствительность прогноза к динамике исходных данных, то высокие значения вполне оправданы.

Отметим, что при расчётах по модели (1.1) встаёт проблема определения прогнозного значения на начальный период (при t = 1, т.е. f₀). Обычно за f₀ берут либо y₁, либо среднее значение нескольких первых членов ряда. Как правило, на конечный результат расчётов выбор начального значения f₀ практически не сказывается.

Приведём пример использования экспоненциально взвешенных скользящих средних. Рассмотрим (рисунок 1.7). Верхняя левая часть этого рисунка – это график исходного ряда, верхняя правая – экспоненциально взвешенная скользящая средняя с = 0,6, нижняя левая – с = 0,3 и нижняя правая – с = 0,1. Как видим, чем больше , тем более гладкий ряд экспоненциально взвешенных скользящих средних.

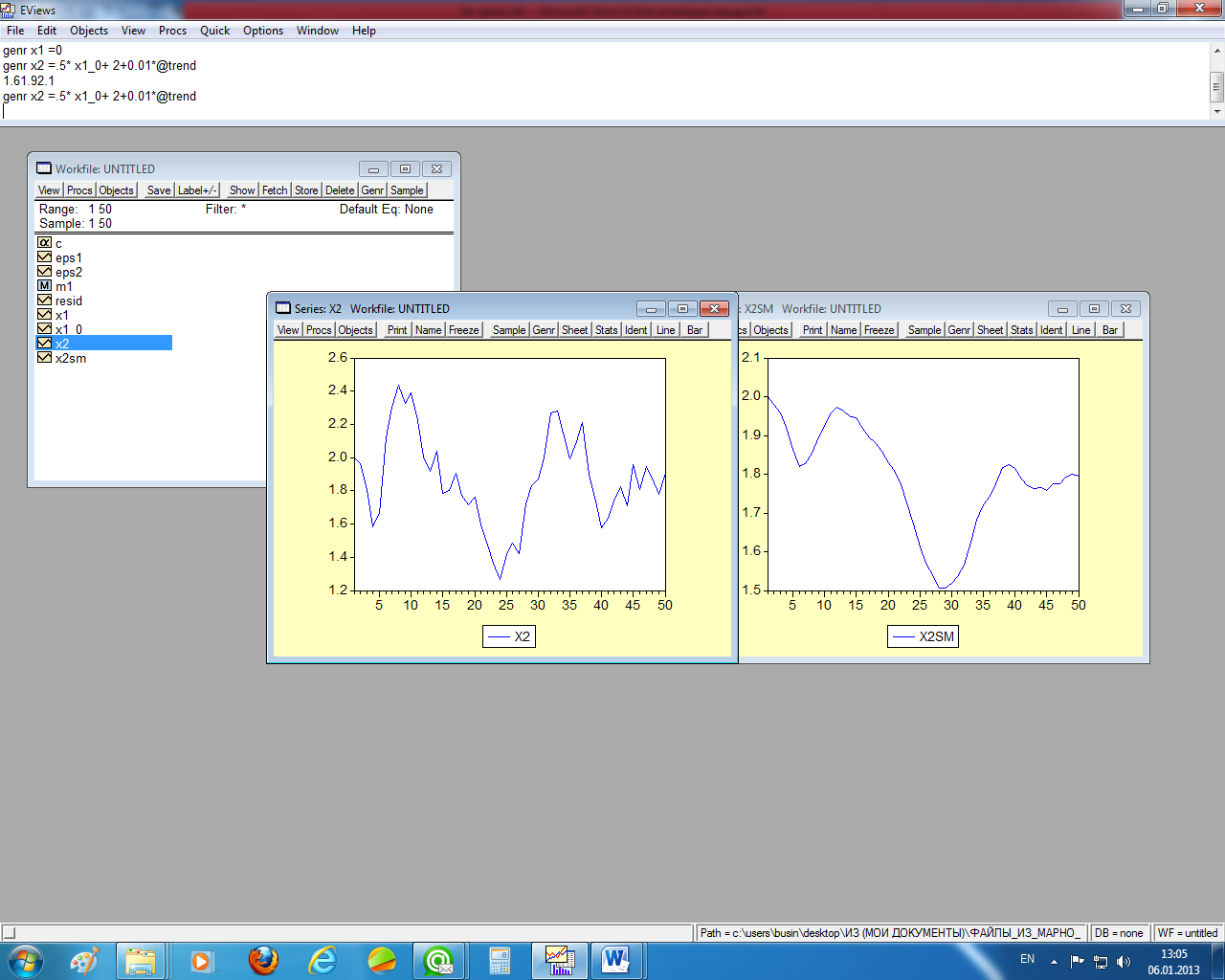
Рисунок 1.7 – Экспоненциально взвешенные скользящие средние