
Леонтева Сборник лабораторныкх работ по физике Молекулярная физика 2015
.pdf
откуда для средних скоростей в горизонтальном и вертикальном направлениях:
 υx
υx  =
=  υy
υy  ~ λg .
~ λg .
Среднюю длину свободного пробега частиц λ определим как отношение расстояния L, пройденного частицей вдоль доски, к числу столкновений с гвоздями на этом расстоянии N:
λ = L/N.
r+a
r+a
a
Рис. 23.П1
Число столкновений найдём следующим образом. Если радиус частицы a, радиус гвоздя r, а число гвоздей на единицу площади доски n, то частица в своём движении столкнётся со всеми теми гвоздями, которые находятся от траектории частицы на расстояни- ях не превышающих r + a (см. рис. 23.П1).
Таких гвоздей на пути длиной L будет
N = 2(a+r) n L.
Тем самым,
λ = |
1 |
. |
|
||
|
||
|
2(a + r) |
|
Если гвозди образуют квадратную решётку (расположены в уг- лах квадратной сетки со стороной R), то, очевидно, расстояние между гвоздями R и их число на единицу площади n связаны соот- ношением nR2 = 1. Если решётка не квадратная, то точного равен- ства уже не будет, но порядок величины nR2 останется прежним. Поэтому
λ ~ |
R2 |
|
|
. |
|
|
||
2(a + r)
Тогда для средних скоростей получаем:
υx ~ υy ~ R |
g |
|
|
. |
|
|
||
|
a + r |
|
41 |
|
|
Итак, средняя скорость частиц пропорциональна расстоянию между гвоздями.
Рассмотрим теперь, как высота доски h должна быть связана с расстоянием между гвоздями R.
В нашем опыте измеряется не скорость, а смещение частицы в горизонтальном направлении x = υxτ, где τ – среднее время движе- ния частицы по доске. Для того чтобы можно было сравнивать ско- рости движения частиц по разным доскам необходимо, чтобы вре- мя движения τ частицы по разным доскам было одинаковым. Но
τ= h/ υy , и поскольку υy ~ R, то
τ~ h/R.
Как видим, для постоянства τ необходимо при изменении рас- стояния между гвоздями пропорционально изменять и высоту дос- ки. В нашем опыте имеются две сменные доски, у которых рассто- яния между гвоздями отличаются вдвое, соответственно и высоты этих досок отличаются вдвое.
42
2. ВЯЗКОСТЬ ГАЗОВ И ЖИДКОСТЕЙ
ВВЕДЕНИЕ К РАБОТАМ № 24–26
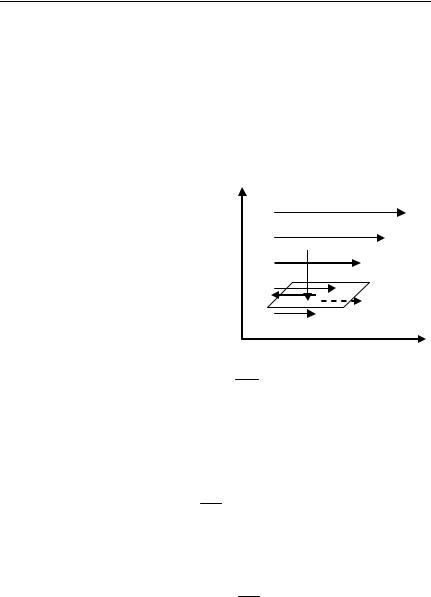
Если в потоке жидкости или газа, который движется в направлении оси ОХ, скорость изменяется в направлении оси OZ (рис. 2.1), то наличие вязкости проявляется в том, что в потоке возникают силы, стремящиеся выровнять скорости среды. Это означает, что силы вязкости стремятся замедлить быстро движущиеся слои и ускорить медленно движущиеся.
Иными словами, наличие вяз- |
z |
|
|||
кости приводит к передаче им- |
|
||||
|
|
||||
пульса от быстрых слоёв к мед- |
|
υ |
|||
ленным. Величина импульса, пе- |
|
|
|||
редаваемого в одну секунду через |
|
П |
|||
единичную площадку, |
называется |
|
|||
|
|
||||
плотностью |
потока импульса П. |
fx |
|
||
Она связана с вязкостью среды η и |
fx |
||||
|
|||||
быстротой |
изменения |
скорости |
|
x |
|
потока υx вдоль оси OZ соотноше- |
|
||||
|
|
||||
нием:
Рис. 2.1
Π = −η dυx . dz
Знак минус здесь соответствует тому, что импульс передаётся в направлении убывания υ, т.е. от быстрых слоёв к медленным. Это соотношение можно записать иначе, если учесть, что согласно вто- рому закону Ньютона импульс, переданный телу в единицу време- ни, равен силе, действующей на это тело:
d P = F. d t
Тогда из определения П ясно, что эта величина есть не что иное, как сила, действующая на единичную площадку параллельную скорости потока:
fтр = −η dυx . dz
43

Для быстрых слоёв – это сила торможения, для медленных – ускоряющая. Из выражения для силы торможения нетрудно опре- делить размерность вязкости:
[η] = Н с/м2 = Па с (CИ),
[η] = г/(с см2) = Пз (пуаз) (СГСЕ). Вязкость идеального газа определяется соотношением:
η= 1 ρυλ, 3
где ρ – плотность газа, υ – средняя скорость теплового движения молекул, λ – средняя длина свободного пробега молекул.
Одним из способов определения вязкости является способ, ос- нованный на использовании формулы Пуазейля:
V = π P R4 t , 8 L η
где V – объем газа или жидкости, протекающей за время t по круг- лой трубе длины L и радиуса R, на концах которой имеется раз- ность давлений P. Эта формула справедлива при сравнительно малых скоростях потока, когда среду можно считать несжимаемой, а поток ламинарным. Поток в трубе является ламинарным, если число Рейнольдса
Re = ρυR
η
не слишком велико (ρ – плотность жидкости или газа, η – её вяз- кость, υ – средняя скорость потока, R – радиус трубы). В круглой трубе поток остаётся ламинарным, пока число Рейнольдса не пре- вышает 1000:
Re = ρυR < 1000.
η
Если среда обладает большой вязкостью, то такую вязкость удобно определять, измеряя силы сопротивления, действующие на тело, движущееся в среде. При малых скоростях движения (малых числах Рейнольдса) эти силы пропорциональны размерам тела, его скорости и вязкости среды:
Fсопр = const η υ a,
где a – характерный размер тела.
44

Для тела сферической формы const = 6π, a = R, где R – радиус тела, и тогда сила сопротивления
Fсопр = 6π ηυ R.
Это соотношение носит название формулы Стокса.
Если скорость потока становится настолько велика, что число Рейнольдса оказывается большим (обычно Re > 1000), то поток становится турбулентным. Это проявляется в том, что в потоке об- разуются многочисленные вихри различных размеров (рис. 2.2). Вследствие этого все характеристики потока в каждой его точке, такие, как скорость, давление, плотность и т.п., испытывают хаоти- ческие пульсации и поэтому изменяются как от точки к точке, так и во времени совершенно нерегулярно.
Рис. 2.2
Следует иметь в виду, что большинство течений жидкостей и газов турбулентны как в природе (атмосферные, речные и океан- ские течения) так и в различных технических устройствах (трубы, каналы, турбины, струи, образованные движущимися судами и т.п.). Большая величина числа Рейнольдса означает, что роль вяз- кости мала. Это, в свою очередь, означает, что силы сопротивле- ния, действующие на тело, находящееся в потоке жидкости или га- за, уже не зависят от вязкости. В этом случае выражение для силы сопротивления следует заменить на другое:
Fсопр = constρυ2 R2.
Причиной возникновения силы сопротивления в этом случае яв- ляется турбулентный след за телом. В области следа средняя ско- рость движения жидкости оказывается меньше, чем перед телом, что означает потерю импульса жидкостью. Потерянный жидкостью
45
импульс передаётся телу, что и вызывает возникновение силы со- противления. Кинетическая энергия поступательного движения жидкости при этом частично переходит в энергию пульсационного движения в турбулентном следе. Без подвода энергии извне турбу- лентные потоки затухают, так как энергия потока передаётся от крупных вихрей к вихрям все более и более малого размера, где роль вязкости уже достаточно велика. Так что в конечном итоге потери энергии и в турбулентном потоке определяются вязкостью.
Работа № 24
ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ВОЗДУХА ПО ИСТЕЧЕНИЮ ИЗ КАПИЛЛЯРА
Цель работы: определить вязкость и длину свободного пробега молекул воздуха.
Приборы и принадлежности: установка для создания равномер- ного потока газа, манометр, осушитель воздуха, секундомер, тер- мометр.
Описание установки и методика измерений
Установка для измерения вязкости воздуха изображена рис. 2.3.
Рис. 2.3
46
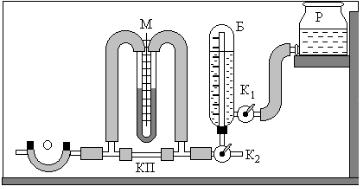
Цилиндрический стеклянный баллон Б при открытом кране К1 может наполняться водой из резервуара Р, если тот поднят выше баллона. При наполнении баллона водой кран К2 должен быть по- вернут в положение а (рис. 2.4), чтобы воздух из баллона мог вы- ходить в атмосферу. Если кран К2 перевести в положение б и опу- стить резервуар вниз, то вода из баллона будет перетекать в резер- вуар Р. С понижением уровня воды в баллоне Б в него будет заса- сываться воздух из атмосферы через осушитель О и капиллярную трубку КП. Измерив объем воздуха V, прошедшего через капилляр за некоторое время t, зная радиус капилляра R, его длину L и раз- ность давлений на его концах P, по формуле Пуазейля можно найти вязкость воздуха
|
πR4 |
P |
|
η = |
1 |
|
t. |
|
|
||
8LV
Рис. 2.4
Для измерения объёма воздуха, протекающего через капилляр- ную трубку, баллон снабжён шкалой, проградуированной в милли- метрах. Так как температуры атмосферного воздуха и воды в бал- лоне одинаковы, то объем вытекающей из него воды равен объёму прошедшего через капиллярную трубку воздуха.
Разность давлений, возникающая на концах капиллярной труб- ки, измеряется при помощи масляного U-образного манометра М, снабжённого шкалой для отсчёта разности уровней масла. Все узлы установки смонтированы на вертикальной раме.
Порядок выполнения работы
1. Подготовьте табл. 2.1.
47
|
|
|
|
|
|
|
|
|
|
Таблица 2.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
№ п/п |
t |
ηi |
|
η |
|
ηi = η i – |
|
|
Δηi2 |
|
Δη |
|
η |
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
2. При закрытом кране К1 |
поставьте резервуар на полку и от- |
||||||||||
крыть кран К2 на атмосферу (положение а). Приоткрыв кран К1, наполните баллон водой.
ВНИМАНИЕ! При наполнении баллона водой нужно следить за тем, чтобы вода не попала в вертикальную трубу, через ко- торую воздух засасывается в баллон. Попадание воды в капил- лярную трубку и масляный U-образный манометр выведет установку из строя.
3.Закрыв кран К1, переставьте резервуар в нижнее положение и поверните кран К2 в положение б. Осторожно приоткройте кран К1
иотрегулируйте сток воды из баллона так, чтобы разность уровней масла в коленах манометра была равна приблизительно 5 см. При таком перепаде давлений течение воздуха через капилляр оказыва- ется ламинарным.
4.Когда уровень воды в баллоне достигнет отметки «0» (1000 мл воды), включите секундомер и измерьте время вытекания 250 мл воды. Вытекание больших количеств воды сопровождается значительным уменьшением перепада давлений.
5.Повторите операции пп. 1–3 и измерения 7 раз. В начале и в конце измерений записать температуру воздуха в помещении. Взять среднее из обоих значений. Занести результаты в табл. 2.1.
6.По окончании работы заглушите систему зажимами от атмо- сферы.
7.Вычислите вязкость воздуха в каждом опыте по формуле Пу- азейля. Перепад давлений на концах капилляра определите из со- отношения
P = P1–P2 = ρмgh,
где ρм – плотность масла в манометре, равная 0,86 г/см3, h – раз- ность уровней масла в коленах манометра.
48
Радиус капилляра и его длина указаны на установке.
8.Определите погрешность Δη.
9.По формуле V = π R2 u t, связывающей объем газа, прошед- ший за время t по капилляру радиуса R, найдите u – среднюю ско- рость течения воздуха в капилляре.
10.Найдите плотность воздуха ρвозд с помощью уравнения со- стояния идеального газа, затем число Рейнольдса для потока воз-
духа Re = ρвозд u R/η, убедитесь в том, что течение воздуха в ка- пилляре имеет ламинарный характер (Re должно быть меньше
1000).
11. |
По температуре Т и массе моля воздуха µ найдите среднюю |
|||||||||
скорость движения молекул воздуха |
|
= |
8RT |
. |
||||||
υ |
||||||||||
|
||||||||||
|
|
|
|
|
|
|
|
πη |
||
12. |
По вязкости воздуха η = |
1 |
ρвозд |
|
λ и средней скорости дви- |
|||||
υ |
||||||||||
|
||||||||||
|
3 |
|
|
|
|
|
|
|
||
жения его молекул υ найдите λ – среднюю длину свободного про-
бега молекул воздуха, а также оцените размер молекулы воздуха.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что называется вязкостью?
2.От каких физических параметров зависит вязкость газа?
3.Какое движение жидкости или газа называется ламинарным?
4.Когда оно превращается в турбулентное?
5.Формула Пуазейля получена в предположении ламинарного тече- ния жидкости по трубе. Как изменится эта формула, если течение станет турбулентным? Для ответа на этот вопрос воспользуйтесь методом раз- мерностей.
49
Работа № 25
ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ КАПИЛЛЯРНЫМ ВИСКОЗИМЕТРОМ ПИНКЕВИЧА
Цель работы: определить вязкость этилового спирта или другой жидкости при данной температуре.
Приборы и принадлежности: капиллярный вискозиметр Пинке- вича, секундомер, термометр, испытуемая жидкость, дистиллиро- ванная вода.
Методика измерений и описание установки
Вданной работе вязкость определяется методом сравнения вре- мени истечения одинаковых объёмов двух жидкостей, вязкость од- ной из которых известна.
Вслучае ламинарного движения жидкости по горизонтальной трубе справедлива формула Пуазейля, связывающая объем жидко- сти V, прошедший за время t по трубе радиуса R и длины L с её
вязкостью η и разностью давлений P на концах трубы:
|
πR4 |
P |
|
V = |
1 |
|
t. |
|
|
||
8ηL
Если сравнить время истечения одинаковых объемов жидкостей (V1 = V2) через один и тот же капилляр (R1 = R2, L1 = L2), то в этом случае
|
P t |
|
|
P t |
2 |
|
|
|
1 1 |
= |
|
2 |
|
, |
|
|
η1 |
η2 |
|
|
|||
|
|
|
|
|
|
||
откуда |
|
|
|
|
|
|
|
|
|
|
|
P t |
|
|
|
|
η = η |
|
1 1 |
. |
|||
|
|
|
|||||
2 |
1 |
|
P2 t2 |
||||
|
|
|
|
||||
В данном опыте жидкость движется по вертикальной трубе под действием силы тяжести. Поэтому вместо силы, вызванной перепа- дом давлений Р на концах трубы, в формулу Пуазейля следует подставить вес столба жидкости, заключённой между сечениями а и b:
P = ρgh.
50
