
ОТЦ / Lab_rab_df
.pdf
Рисунок 9.1 – Принципиальная схема стенда
С помощью гнезд 1-17 и электрических проводников обеспечивается подключение элементов R, L, C к стенду. Схема исследуемой цепи второго порядка (последовательный колебательный контур) представлена на рисунке 9.2.
Рисунок 9.2 – Схема цепи второго порядка
С выхода генератора на вход стенда подаются импульсы напряжения прямоугольной формы, период следования которых Т имеет фиксированную величину и в десять раз превышает период Тсв свободных колебаний исследуемой цепи.
9.3 Сведения из теории
Пусть в момент времени t = 0 к RLC-цепи подключается источник э.д.с. e(t). Уравнение, описывающее переходный процесс, запишется в виде:
R i |
di |
|
1 |
idt e(t). |
(9.1) |
dt |
C |
Дифференцируя это уравнение, получим:
L |
d2i |
R |
di |
|
i |
de |
(9.2) |
||
|
|
|
|
|
|
. |
|||
dt2 |
dt |
|
|
||||||
|
|
|
C |
dt |
|
||||
Соответствующее ему характеристическое уравнение определяется выражением:
Lp2 Rp 1 0.
C
81

Корни этого уравнения:
|
|
|
|
|
R |
|
|
|
|
|
R |
2 |
1 |
|
|
|
|
|
||
|
|
p1,2 |
|
|
|
|
|
|
2 |
2 |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||
2L |
|
|
|
LC |
|
|||||||||||||||
|
|
|
|
|
|
|
2L |
|
|
|
|
|
|
|||||||
где |
R |
; |
0 |
|
|
|
1 |
|
|
– резонансная частота контура. |
||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||||||
|
2L |
|
|
|
|
|
|
LC |
|
|
|
|
|
|
|
|||||
Свободный ток будет равен:
iсв А1 еp1t A2 ep2t ,
где А1 и А2 – постоянные коэффициенты.
Ток в цепи определяется суммой свободного iсв и установившегося iу токов:
i i |
y |
A |
ep1t A |
ep2t . |
(9.3) |
|
1 |
2 |
|
|
Для нахождения iу необходимо знать конкретный вид входного воздействия e(t).
Будем считать, что ко входу цепи подключается источник постоянной э.д.с Е.
Пусть в момент времени t = 0 напряжение на емкости uC(0)=U0 и ток цепи i(0)=0. Для определения постоянных A1 и A2 наряду с независимым начальном условием i(0)=0 необходимо знать и зависимое начальное усло-
вие |
di |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Найдем это условие. Уравнение (9.1) для t = 0 имеет вид: |
|
||||||||||||||||||
|
|
|
|
|
L |
di |
|
|
|
u0 |
E. |
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
dt |
t 0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
di |
|
|
|
|
|
E U0 |
. |
(9.4) |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
dt |
|
t 0 |
|
|
L |
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
При e(t)=Е уравнение (9.2) запишется в виде: |
|
||||||||||||||||||
|
|
|
|
L |
d2i |
|
R |
di |
i |
(9.5) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
0. |
|||||||||
|
|
|
|
dt2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
C |
|
||||||||
Правая часть уравнения (9.5) равна нулю, поэтому и установившееся значение тока цепи iy также будет равно нулю. Дифференцируя выражение (9.3) с учетом iy=0, получим:
82

|
di |
A1 |
p1 ep1t A2 |
p2 ep2t . |
(9.6) |
||||
|
|
||||||||
|
dt |
|
|
|
|
|
|
||
Из выражений (9.3) и (9.6) для t = 0 получим: |
|
||||||||
|
|
0 А А , |
|
|
|
||||
|
|
|
|
1 2 |
|
|
|
||
|
|
|
Е U0 |
A p A p |
. |
|
|||
|
|
|
|
||||||
|
|
|
L |
1 1 |
2 2 |
|
|
||
|
|
|
|
|
|
|
|
||
Откуда следует:
A1 A2 L(Ep1 Up02 ) 2LE
 2U0 02 .
2U0 02 .
Окончательно выражение для тока запишется в виде:
i |
E U0 |
|
(ep1t ep2t ). |
(9.7) |
|
|
|
|
|||
2L 2 2 |
|||||
|
0 |
|
|
|
|
Проанализируем полученное решение для трёх возможных случаев:
а) |
0, т.е. R 2 |
|
|
L |
|
(процесс апериодический); |
||
|
|
C |
||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
б) |
0, т.е. R 2 |
|
|
L |
|
(критический случай); |
||
|
|
C |
||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
в) |
0, т.е. R 2 |
|
|
L |
(процесс колебательный). |
|||
|
|
C |
|
|
||||
Для случая а) корни р1 |
и р2 |
характеристического уравнения являются |
||||||
отрицательными действительными числами (рисунок 9.3). Если р1 р2 ,
то кривая ер1t спадает медленнее, чем кривая ер2t . Кривые i(t) и uC(t) показаны на рисунке 9.4.
Рисунок 9.3 – Расположение действительных корней на комплексной плоскости
83

Рисунок 9.4 – Графики изменения тока цепи и напряжения
на ёмкости в последовательном колебательном контуре при е(t) = E, когда p1 и p2 действительны
Рассмотрим второй случай (случай б).
При |
p p |
2 |
|
R |
. |
|
|||||
0 |
1 |
|
2L |
|
|
|
|
|
|
|
Подстановка этого значения в выражение (9.7) приводит к неопреде-
ленности типа 00. Раскроем ее по правилу Лоппиталя:
i lim |
E U0 |
|
(ep1t ep2t ) |
E U0 |
t e t . |
|
|
|
|
||||
p1 p2 |
L( p p |
2 |
) |
|
L |
|
|
1 |
|
|
|
|
|
Криваятокаi(t)дляэтогослучая имееттакой же вид, какинарисунке9.4. Рассмотрим третий случай (случай в)).
Корни характеристического уравнения комплексные и сопряженные (рисунок 9.5):
p1 j св p2 j св,
где св 
 02 2 .
02 2 .
Корни уравнения располагаются симметрично относительно действительной оси в левой полуплоскости на полуокружности с центром в на-
чале координат и с радиусом |
|
1 |
|
. |
|
|
|
||
|
||||
0 |
|
LC |
||
84

Рисунок 9.5 – Расположение комплексно сопряжённых корней на комплексной плоскости
Величина св называется угловой частотой свободных колебаний в RLC - цепи. Выражение для тока i(t) запишется в виде:
i |
E U0 |
e t sin |
t. |
(9.8) |
|
||||
|
|
св |
|
свL
Кривая зависимости i(t) показана на рисунке 9.6.
Рисунок 9.6 – Графики изменения тока цепи и напряжения на ёмкости в последовательном колебательном контуре при колебательном характере переходного процесса
Из выражения (9.8) и рисунка 9.6 видно, что при 0 в цепи возникают затухающие синусоидальные колебания, причем огибающими
служат кривые E U0 e t . Колебания возникают вследствие перио-
свL
85

дического преобразования энергии электрического поля в энергию магнитного поля и наоборот, причем, эти колебания сопровождаются потерей
энергии в сопротивлении. Чем меньше по сравнению с 0, тем медлен-
нее затухает колебательный процесс и тем ближе св к 0.
О быстроте затухания колебательного процесса судят по величине
e Tсв , |
называемой декрементом колебания, где Тсв |
2 |
. |
Кроме того, |
|
||||
|
|
|
|
|
|
|
св |
|
|
для этих же целей используется логарифмический декремент колебания
Тсв.
Величину 1 называют постоянной времени колебательного контура:
1 2LR
Из сопоставления рисунков 9.3 и 9.5 видно, что о характере переходного процесса можно судить по расположению корней характеристического уравнения на комплексной плоскости. Если корни различны и лежат на действительной оси, то имеет место апериодический процесс. Если p1 p2 , то имеет место критический случай. Для р1 и р2 комплексно сопряженных имеет место колебательный процесс.
9.4 Подготовка к лабораторной работе
9.4.1При выполнении расчетов к лабораторной работе следует считать, что параметры колебательного контура L= 50 мГн и С= 0,1 мкФ остаются неизменными в процессе выполнения работы, а сопротивление R принимает четыре значения: 510 Ом, 1 кОм, 1,5 кОм и 3 кОм.
9.4.2Рассчитать значение критического сопротивления контура: Rкр.
9.4.3Найти корни характеристического уравнения для R = 510 Ом, 1кОм, 1,5 кОм, 3 кОм.
9.4.4Найти частоты свободных колебаний исследуемого контура
св1 для R = 510 Ом и св2 для R=1 кОм.
9.5 Порядок выполнения работы
9.5.1Подключить вход осциллографа к выходу генератора и получить на экране устойчивое изображение 1-2 импульсов напряжения генератора, используя внутреннюю синхронизацию. Период следования импульсов должен быть в 10 раз больше периода свободных колебаний. Определить масштаб изображения.
9.5.2Подключить генератор ко входу последовательного колебательного контура с R = 510 Ом, а вход осциллографа – к выводам конденсатора С. Зарисовать полученную осциллограмму.
86
9.5.3Повторить п.п. 9.5.1, 9.5.2 для R = 1 кОм ( св2 ).
9.5.4Повторить п. 9.5.3 для R = 1,5 кОм.
9.5.5Повторить п. 9.5.3 для R = 3 кОм.
9.6 Обработка результатов
9.6.1 На основании полученных осциллограмм напряжения найти частоты свободных колебаний СВ1Э , СВ2Э и критическое сопротивление
RКРЭ . Сравнить их с расчетными значениями.
9.6.2Определить корни характеристического уравнения, соответствующие экспериментальным кривым в колебательном режиме. Сравнить их со значениями, найденными расчетным путем.
9.6.3Вычислить абсолютные и относительные погрешности полученных результатов.
Контрольные вопросы:
1.Чем определяется порядок цепи при расчете переходных процессов?
2.В каких случаях свободная составляющая напряжения на конденсаторе имеет колебательный характер, а в каких – апериодический?
3.Чем определяется частота свободных колебаний контура?
4.Как определяется постоянная времени последовательного колебательного контура?
5.Чем определяется декремент затухания и логарифмический декремент затухания колебаний?
6.Можно ли избежать возникновения переходного процесса в последовательном колебательном контуре?
7.В чем заключается преимущество и недостатки классического метода расчета переходных процессов?
8.Как изменится величина , если увеличить:
–сопротивление контура R;
–индуктивность L;
–ёмкость С?
9.Чем определяется длительность переходного процесса в последовательном колебательном контуре?
10.Как связан характер протекания переходного процесса в последовательном колебательном контуре с расположением корней характеристического уравнения на комплексной плоскости?
Рекомендуемая литература
[1, с. 87–295; 2, c. 346–362; 3, c. 427–445].
87
Лабораторная работа № 10 ИССЛЕДОВАНИЕ РАЗВЕТВЛЕННОЙ ЭЛЕКТРИЧЕСКОЙ
ЦЕПИ С ОДНИМ ИСТОЧНИКОМ ПОСТОЯННОГО ТОКА
10.1Цель работы: освоение методов эквивалентного преобразования электрической цепи; проведение опытной проверки аналитического расчета цепи с использованием законов Ома и Кирхгофа и подтверждение
вих справедливости.
10.2Оборудование и материалы: стенд, оборудованный источниками постоянного и переменного токов, щитовыми электроизмерительными приборами, наборами резисторов, конденсаторов и ключей, гнездами, сигнальными лампочками. Электропитание стенда осуществляется от силового щита лаборатории, содержащего разделительный трансформатор, коммутационную аппаратуру, устройства защиты и световой сигнализации. Конкретная схема исследуемой цепи собирается с помощью проводников, элементов и приборов стенда. При этом необходимо помнить о соблюдении полярности подключения амперметров и вольтметров постоянного тока и правильном выборе пределов измерения приборов.
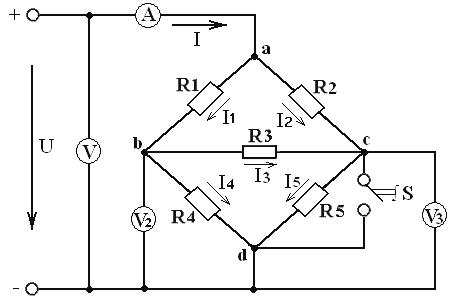
Принципиальная электрическая схема исследуемой цепи представлена на рисунке 10.1.
Рисунок 10.1 – Электрическая схема разветвлённой цепи постоянного тока
88
10.3 Сведения из теории
Расчет линейных разветвленных электрических цепей с одним источником постоянного тока проводят с использованием законов Ома и Кирхгофа.
Эквивалентное сопротивление цепи RЭ с входным током I при подключении к её входу напряжения U определяется законом Ома:
RЭ |
|
U |
. |
(10.1) |
|
||||
|
|
I |
|
|
Применяя первый закон Кирхгофа для узлов разветвления цепи, а второй закон Кирхгофа для отдельных контуров разветвленной цепи (при известных величинах I, U и сопротивлений ветвей Ri) находят токи, напряжения, мощности на отдельных участках. До записи уравнений по законам Кирхгофа на схеме цепи стрелкой указывают условно положительные направления токов в ветвях. Эти условно положительные направления токов выбирают произвольно.
Первый закон Кирхгофа: алгебраическая сумма токов в узле раз-
ветвления равна нулю. Физически первый закон Кирхгофа выражает закон сохранения заряда. Если с узлом исследуемой цепи соединено n ветвей, то уравнение по первому закону Кирхгофа для него будет иметь вид:
n |
|
|
Ii |
0. |
(10.2) |
i 1 |
|
|
При этом втекающие в узел токи выбирают со знаком «плюс», а токи, вытекающие из узла, – со знаком «минус». (Допускается использование и обратного правила выбора знаков токов). При расчёте цепи уравнения по первому закону Кирхгофа записываются только для независимых узлов. Их число всегда на 1 меньше общего количества узлов. Например, если электрическая цепь имеет q узлов, то число независимых узлов будет рав-
но q-1.
Второй закон Кирхгофа: при обходе контура электрической цепи
в любом направлении алгебраическая сумма падений напряжений на электрических элементах контура (сопротивлениях, индуктивностях, ёмкостях) равна алгебраической сумме действующих в контуре э.д.с.
Направление обхода контура выбирается произвольно и указывается внутри контура стрелкой. Если контур содержит l источников э.д.с. и k электрических элементов, то уравнение по второму закону Кирхгофа запишется для него в виде:
l |
k |
|
En |
Ii Ri . |
(10.3) |
n 1 |
i 1 |
|
Вуравнениях по второму закону Кирхгофа напряжения на элементах
иэ.д.с. источников выбираются со знаком «плюс», если их положительно
89
выбранные направления совпадают с направлением обхода контура. В противном случае их величины берутся со знаком «минус». Уравнение второго закона Кирхгофа для контура, не содержащего источников э.д.с., запишется в виде:
k
Ii Ri 0.
i 1
Число расчетных уравнений по второму закону Кирхгофа определяется количеством независимых контуров n, которое рассчитывается по числу ветвей р и числу узлов q схемы цепи:
n p (q 1). |
(10.4) |
Решив совместно уравнения, составленные по законам Кирхгофа, определяют токи в отдельных ветвях. Если при решении получится отрицательное значение тока той или иной ветви, то этот ток имеет направление, обратное указанному на схеме.
Наряду с методом, основанным на использовании законов Кирхгофа, для расчёта разветвлённой электрической цепи используют метод эквивалентных преобразований. По этому методу всю схему разбивают на отдельные участки, содержащие только последовательно соединённые или только параллельно соединённые элементы. Находят эквивалентные сопротивления таких участков и, учитывая способ соединения их между собой, эквивалентное сопротивление всей цепи и её ток. Далее, используя закон Ома, находят необходимые напряжения между узлами и токи ветвей. В методе эквивалентных преобразований схема исходной разветвлённой электрической цепи заменяется более простыми схемами цепей, которые имеют такое же эквивалентное сопротивление.
Если схема разветвлённой цепи содержит участки, в которых элементы соединены по схеме «Звезда» (сопротивления Ra, Rb, Rc рисунка 10.2а) или «Треугольник» (сопротивления R1, R2, R3 рисунка 10.2б), то для расчёта эквивалентного сопротивления цепи преобразуют «Звезду» в «Треугольник» или наоборот.
Эквивалентным преобразованием «Треугольника» в «Звезду» называется такая замена части цепи, соединённой по схеме «Треугольник», цепью, соединённой по схеме «Звезда», при которой токи и напряжения в остальной части цепи остаются неизменными. Иначе говоря, при одинаковых напряжениях между одноимёнными узлами входящие в них токи одинаковы и для «Треугольника», и для «Звезды». То есть мощности в этих цепях одинаковы. Преобразование «Треугольника» в «Звезду» производится по формулам:
Ra |
|
|
R1R2 |
; |
Rb |
|
R1R3 |
; |
Rс |
|
R2R3 |
. (10.5) |
|||||
R |
R |
2 |
R |
R |
R |
2 |
R |
R |
R |
R |
|||||||
|
1 |
|
3 |
|
|
1 |
|
3 |
|
|
1 |
2 |
3 |
|
|||
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
