2.3 Задачи

1НТ1(З) При β >> ω₀ и ω₀ = 10 амплитуда отклонения осциллятора при его свободной релаксации изменилась в «е» раз за время t = 1с коэффициент затухания β = …

Ответ : 50

2НТ1(О) При β >> ω0 и β = 20 амплитуда отклонения осциллятора от положения равновесия уменьшилась в «е» раз за время t = 10^-1 с собственная частота осциллятора равна

ω0 = …

Ответ : 2

3НТ3(З) Известно , что в общем случае апериодический процесс релаксации описывается двумя слагаемыми, одно из которых убывает при β >> ω₀ существенно быстрее другого. Если собственная частота осциллятора , а более «медленное» слагаемое убывает в «е» раз за t = 0,2 с . То пренебречь быстро убывающим слагаемым можно уже при t >>…

А) c

В) 0,05 с

С) 0,01 с

*D) 0,1 с

4НТ1(О) Если собственная частота колебаний диссипативного осциллятора равна ω₀ = 10 , то критический режим процесса релаксации будет иметь место при β = ….с^-1

Ответ : 10

5НТ1(О) В электрическом контуре Гн, С = 1МкФ критический режим процесса релаксации тока после отключения контура от источника будет иметь место при R = … Ом

Ответ: 2

6НТ1(З) Для того, чтобы в RLC контуре имели место колебания при R= 20 Ом и С = 1 МкФ, индуктивность должна быть больше L > … Гн

*А) В) С) D)

7НТ1(О) Частота свободных затухающих колебаний диссипативного осциллятора равна 4 , а собственная частота 5

Коэффициент затухания осциллятора равен β =…

Ответ: 3

8НТ1(О)Циклическая частота свободных затухающих колебаний в RLC контуре с сопротивлением R = 6 Ом равна 4 , а собственная частота 5 .

Индуктивность контура равна L =… Гн

Ответ:1

9НТ2(З)

Начальна фаза в RLC контуре = 30^о сдвиг среды между током и напряжением на U_L = 100^о векторная диаграмма колебаний имеет вид:

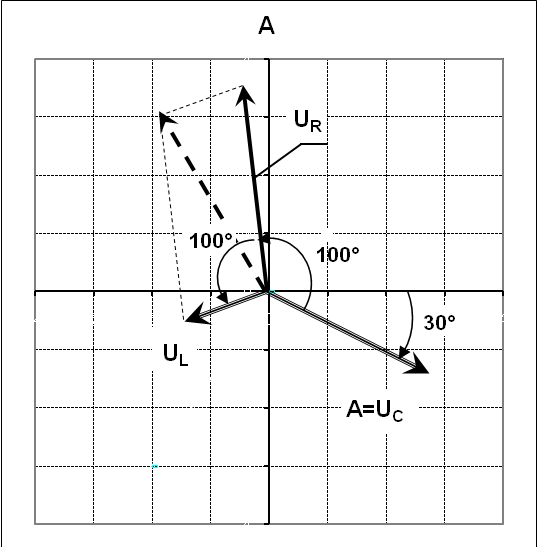
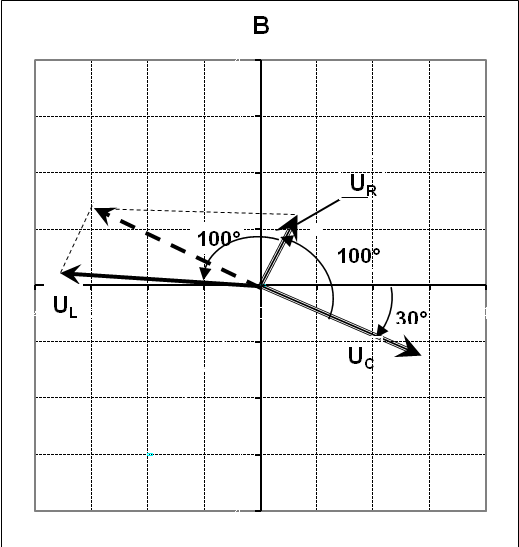
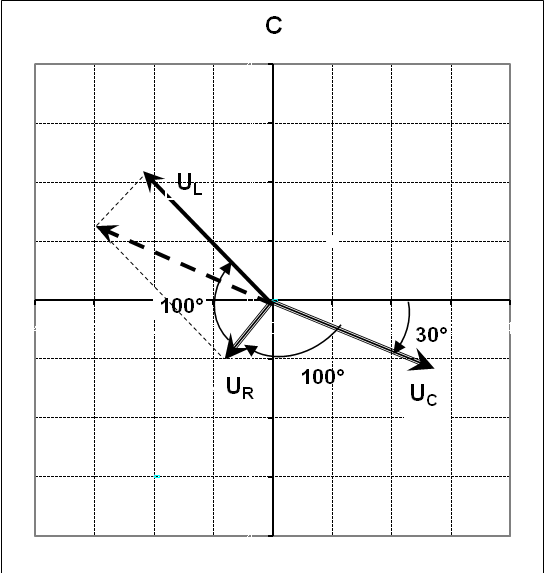
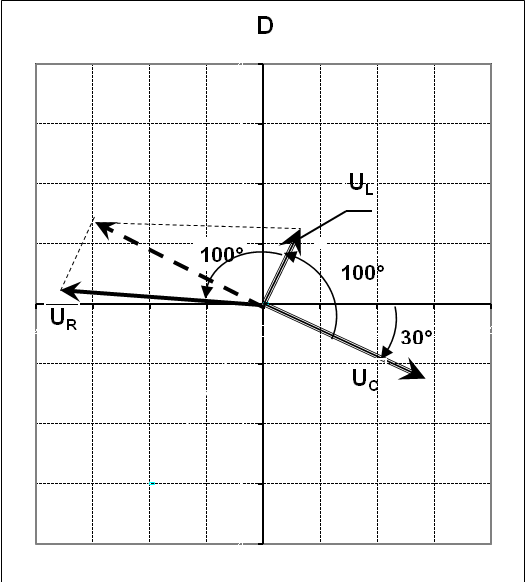
Ответ: В

10НТ2(О) Отношение квадратов циклической частоты затухающих колебаний к коэффициенту затухания равно 3. Сдвиг фазы между напряжением на конденсаторе и током в RLC контуре равен(в градусах)…

Ответ: 150

11НТ2(О) На рисунке приведена векторная диаграмма затухающих колебаний для некоторого момента времени в RLC контуре, циклическая частота колебаний ω = 10

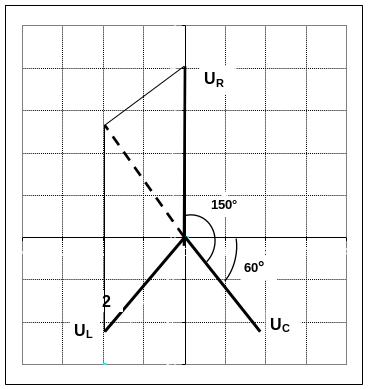
Коэффициент затухания контура равен β = …

Ответ: 10

12НТ2(О) На рисунке приведена векторная диаграмма затухающих колебаний для некоторого момента времени в RLC контуре, циклическая частота колебаний ω = 10

Индуктивность контура L = 0,1 Гн.

Сопротивление контура R = … Ом

Ответ: 2

13НТ1(О)В пружинном маятнике коэффициент силы сопротивления равен r₀ = 0,4 , а коэффициент затухания . если частота свободных колебаний маятника ω₀ = 20 , то коэффициент упругости пружины k = …,

Ответ: 40

14НТ1(З) Колебательная функция некоторого диссипативного осциллятора имеет вид . График функции приведён на рисунке…

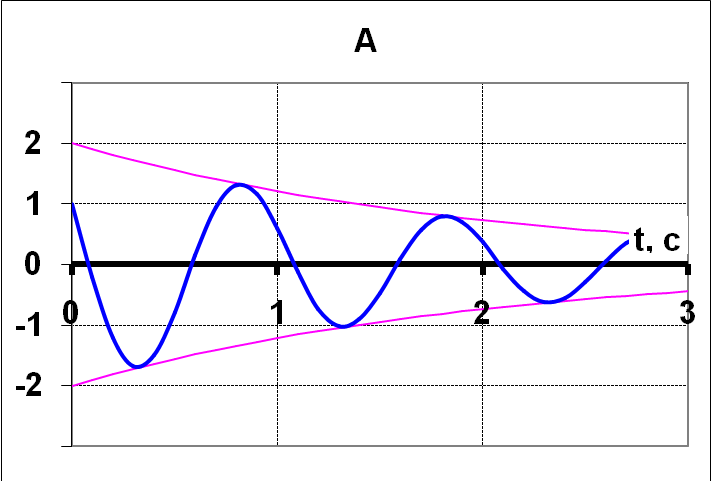
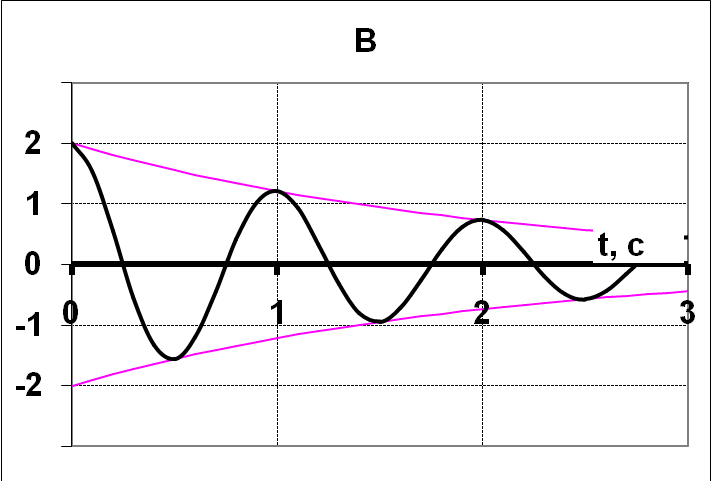
Ответ: А

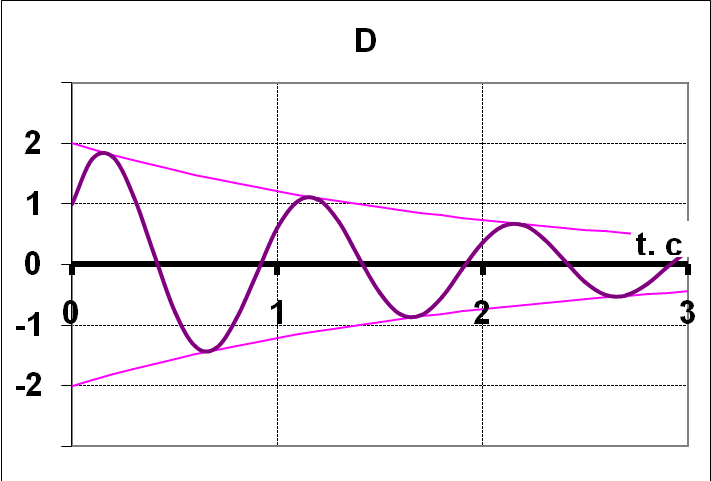
15НТ1(З)Колебательная функция некоторого диссипативного осциллятора имеет вид . График функции приведён на рисунке:

Ответ: D

16НТ1(О) Параметры электрического колебательного контура равны L = 2 мГн, С = 0,2 мкФ, R = 2 π Ом. Амплитуда свободных затухающих колебаний в контуре уменьшится в «e» раз после изменения фазы колебаний на … рад

Ответ: 50

17НТ2(О) Параметры электрического колебательного контура равны L = 2 мГн, С = 0,2 мкФ, R = 2 Ом.

Число колебаний за которое амплитуда колебаний уменьшится в «е» раз равно…

Ответ:50

18НТ2(О) Параметры электрического колебательного контура равны L = 2 мГн, С = 0,2 мкФ, R = 2 π Ом. Число свободных колебаний , за которое энергия колебаний уменьшится в «е» раз равно…

Ответ: 25

19НТ1(О) в электрическом контуре с индуктивностью L = 10^-2 Гн и емкостью С = 5 мкФ .

амплитуда электрического заряда в контуре при свободных гармонических колебаниях q_m = 10^-2 Кл.

Энергия колебаний заряда в контуре равна… Дж

Ответ: 1

20НТ1(З) Если логарифмический декремент Δ = 0,02, то энергия колебаний уменьшится в е раз через N полных колебаний

A)N = 50

B)N = 100

*C) N = 25

D) N = 250

21.HT1(З) Если за 50 полных колебаний энергия системы уменьшилась в е раз, то логарифмический декремент системы равен:

A)0,01

B) 0,02

C) 0,05

D) 0,5

22НТ2(З) Логарифмический декремент Δ, при котором энергия колебательного контура за N полных колебаний уменьшилась в m раз , равен:

A)

B)

C)

D)

23HT2(з) Амплитуда затухающих колебаний системы с добротностью θ - 100π уменьшится в е раз через число колебаний N_e, равное

A) 10

*B) 100

C) 50

D) 200

24НТ2(з) Энергия затухающих колебаний системы с добротностью θ - 100π уменьшится в е раз через число колебаний N, равное

A) 10

B) 100

*C) 50

D.)200

25НТ2(З) Добротность осциллятора, в котором амплитуда колебаний уменьшается в г раз через 100 периодов, равна:

A) 100

B) 100π

C) 50π

D) 200

26НТ2(З) Фаза колебаний осциллятора изменилась на ∆φ = 50π при уменьшении его энергии в е раз. Добротность осциллятора равна:

А) 50

В) 100π

*С) 50 π

D) 100

27НТ1(З) Добротность θ колебательного контура, состоящего из катушки с индуктивностью L = 2мГн, конденсатора с емкостью C = 0,2мкФ и резистора с сопротивлением R = 1 Ом , равна:

	A.	50
	B.	75
*	C.	100
	D.	200