
- •1.Что такое Всеобщее управление качеством?
- •2. История развития систем управления качеством
- •3.Основные принципы tqm.
- •4.Показатели качества продукции
- •5. Петля качества.
- •6.Цикл Деминга
- •Этапы жизненного цикла продукта и правило 10-кратных затрат
- •Три основных пути конкурентной борьбы.
- •11.Имидж компании, айсберговый эффект
- •12.Теория вариаций
- •13.Понятие размаха вариации.
- •14.Понятие среднего линейного отклонения.
- •15.Статистические методы контроля качества
- •16.Нормальный закон распределения.
- •17.Функция Лапласа
- •18.Правило трех сигм
- •19.Контрольный листок
- •20.Гистограмма
- •21.Диаграмма разброса
- •22.Диаграмма Парето.
- •23.Расслаивание (стратефикация).
- •24.Диаграмма Исикавы
- •Контрольная карта
- •Семь инструментов управления качеством
- •27.«Мозговая атака» («штурм, осада»)
- •28. Диаграмма сродства
- •29. Диаграмма связей
- •30.Древовидная диаграмма
- •31.Матричная диаграмма (таблица качества)
- •32. Стрелочная диаграмма
- •33.Процессный подход согласно стандартов исо 9000
- •34.Кружки качества.
- •35.Qfd (технология развертывания функций качества)
- •36.Профиль качества
- •37.Дом качества
- •38.Структура фаз в методе сфк
- •39.Типы улучшения качества «Кайрио» и «Кайзен»
- •40.Управление процессом по Джурану
- •41.Функции менеджмента качества
20.Гистограмма
Для наглядного представления тенденции изменения наблюдаемых значений применяют графическое изображение статистического материала. Наиболее распространенным графиком, к которому прибегают при анализе распределения случайной величины при проведении контроля качества, является гистограмма.
Для построения гистограммы распределения, используется контрольный листок (таблица накопленных частот) который включает в себя следующие графы: (см.табл.).
Таблица - Таблица накопленных частот
Номер интервала |
Границы интервала |
Абсолютная
частота
|
Относительная
частота
|
|
нижняя |
верхняя |
|||
1 |
1,65 |
1,77 |
2 |
0,02 |
2 |
1,77 |
1,89 |
3 |
0,03 |
3 |
1,89 |
2,01 |
6 |
0,06 |
4 |
2,01 |
2,13 |
12 |
0,12 |
5 |
2,13 |
2,25 |
26 |
0,26 |
6 |
2,25 |
2,37 |
28 |
0,28 |
7 |
2,37 |
2,49 |
11 |
0,11 |
8 |
2,49 |
2,61 |
5 |
0,05 |
9 |
2,61 |
2,73 |
4 |
0,04 |
10 |
2,73 |
2,85 |
2 |
0,02 |
Сумма |
|
|
100 |
1 |
|
|
|
|
|
Гистограмма — это инструмент, позволяющий зрительно оценить закон распределения статистических данных.
Гистограмма распределения обычно строится для интервального изменения значения параметра. Для этого на интервалах, отложенных на оси абсцисс, строят прямоугольники (столбики), высоты которых пропорциональны частотам интервалов. По оси ординат откладывают абсолютные значения частот (см. рисунок). Аналогичную форму гистограммы можно получить, если по оси ординат отложить соответствующие значения относительных частот. При этом сумма площадей всех столбиков будет равна единице, что оказывается удобно. Гистограмма также очень удобна для визуальной оценки расположения статистических данных в пределах допуска. Чтобы оценить адекватность процесса требованиям потребителя, мы должны сравнить качество процесса с полем допуска, установленным пользователем. Если имеется допуск, то на гистограмму наносят верхнюю и нижнюю его границы в виде линий, перпендикулярных оси абсцисс, чтобы сравнить распределение параметра качества процесса с этими границами. Тогда можно увидеть, хорошо ли располагается гистограмма внутри этих границ.
На основании контрольного листка строится гистограмма, или, при большом количестве измерений, кривая распределения плотности вероятностей.
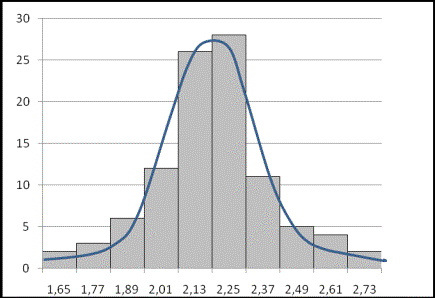
Рисунок – Гистограмма
