
- •1.Что такое Всеобщее управление качеством?
- •2. История развития систем управления качеством
- •3.Основные принципы tqm.
- •4.Показатели качества продукции
- •5. Петля качества.
- •6.Цикл Деминга
- •Этапы жизненного цикла продукта и правило 10-кратных затрат
- •Три основных пути конкурентной борьбы.
- •11.Имидж компании, айсберговый эффект
- •12.Теория вариаций
- •13.Понятие размаха вариации.
- •14.Понятие среднего линейного отклонения.
- •15.Статистические методы контроля качества
- •16.Нормальный закон распределения.
- •17.Функция Лапласа
- •18.Правило трех сигм
- •19.Контрольный листок
- •20.Гистограмма
- •21.Диаграмма разброса
- •22.Диаграмма Парето.
- •23.Расслаивание (стратефикация).
- •24.Диаграмма Исикавы
- •Контрольная карта
- •Семь инструментов управления качеством
- •27.«Мозговая атака» («штурм, осада»)
- •28. Диаграмма сродства
- •29. Диаграмма связей
- •30.Древовидная диаграмма
- •31.Матричная диаграмма (таблица качества)
- •32. Стрелочная диаграмма
- •33.Процессный подход согласно стандартов исо 9000
- •34.Кружки качества.
- •35.Qfd (технология развертывания функций качества)
- •36.Профиль качества
- •37.Дом качества
- •38.Структура фаз в методе сфк
- •39.Типы улучшения качества «Кайрио» и «Кайзен»
- •40.Управление процессом по Джурану
- •41.Функции менеджмента качества
12.Теория вариаций
Теория вариаций – базируются на следующих положениях:
Следует понимать природу вариаций, включая оценку стабильности системы, а также представление о случайных и закономерных изменениях.
Вариации постоянно происходят в обществе, производстве, обслуживании, продукте. Что же эти изменения могут нам сказать о процессе и людях, занятых в нем?
Следует понимать возможности процесса. Какие должны быть его результаты, чтобы сделать выводы о его стабильности? Стабильный статистический подконтрольный процесс имеет совершенно определенные возможности.
Поведение процесса полностью различно в двух случаях: стабильном и не стабильном. Ошибка в распознавании этих двух состояний ведет к катастрофе.
Знание об этих различиях основано на оценке уверенного поведения управляемой системы. Управляемая система стабильна в статистическом смысле.
При попытке усовершенствования процесса возможны два рода фатальных ошибок:
исправлять как закономерное изменение любые отклонения, ошибки, когда на самом деле эти изменения носят случайный характер;
классифицировать как случайное изменение какую-либо ошибку, отклонение, когда на самом деле происходит закономерное изменение.
Следует знать действия, нацеленные на минимизацию потерь от этих двух ошибок.
Необходимо знать, какое вмешательство может усилить воздействие либо свести его к нулю. В любом случае эффективность любой системы зависит от вмешательства человека. Важно все знать о взаимодействии между людьми, группами, подразделениями, компаниями, странами.
Знание о функции потерь должно содержать информацию об условиях оптимизации системы. Следует обратить особое внимание на характеристики качества.
Необходимо знать о потерях, которые возникают в результате случайных воздействий или изменений.
13.Понятие размаха вариации.
Размах
вариации
это разница между максимальным и
минимальным значением.
![]()
С одной стороны показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе проч. С другой стороны, размах может быть очень широким и не иметь практического смысла.
Ниже приведена графическая интерпретация размаха вариации.
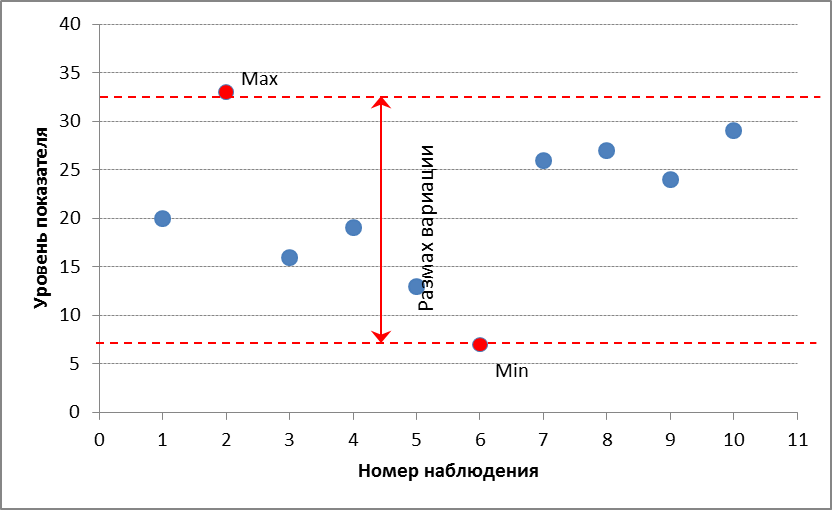
Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
Данный показатель не дает устойчивую оценку, так как все зависит от двух, как правило, случайных значений – от максимума и минимума. Таким образом, размах вариации очень неустойчивая величина.
14.Понятие среднего линейного отклонения.
Среднее линейной отклонение характеризует меру разброса значений совокупности данных вокруг их среднего значения. В чем суть? Для того, чтобы показать меру разброса данных нужно вначале определиться, относительно чего этот самый разброс будет считаться. Обычно это средняя величина. Дальше нужно посчитать, насколько значения анализируемой совокупности данных находятся далеко от средней. Понятное дело, что каждому значению соответствует некоторая величина отклонения, но нас же интересует общая оценка, охватывающая всю совокупность. Поэтому рассчитывают среднее отклонение по формуле обычной средней арифметической. Но! Но для того, чтобы рассчитать среднее из отклонений, их нужно вначале сложить. И если мы сложим положительные и отрицательные числа, то они взаимоуничтожатся и их сумма будет стремиться к нулю. Чтобы этого избежать, все отклонения берутся по модулю, то есть все отрицательные числа становятся положительными. Вот теперь среднее отклонение будет показывать обобщенную меру разброса значений. В итоге, средне линейное отклонение будет рассчитываться по формуле:
![]()
где
a – среднее линейное отклонение,
x – анализируемый показатель, с черточкой сверху – среднее значение показателя,
n – количество значений в анализируемой совокупности данных,
Рассчитанное
по указанной формуле среднее линейное
отклонение отражает среднее абсолютное
отклонение от средней величины по данной
совокупности.
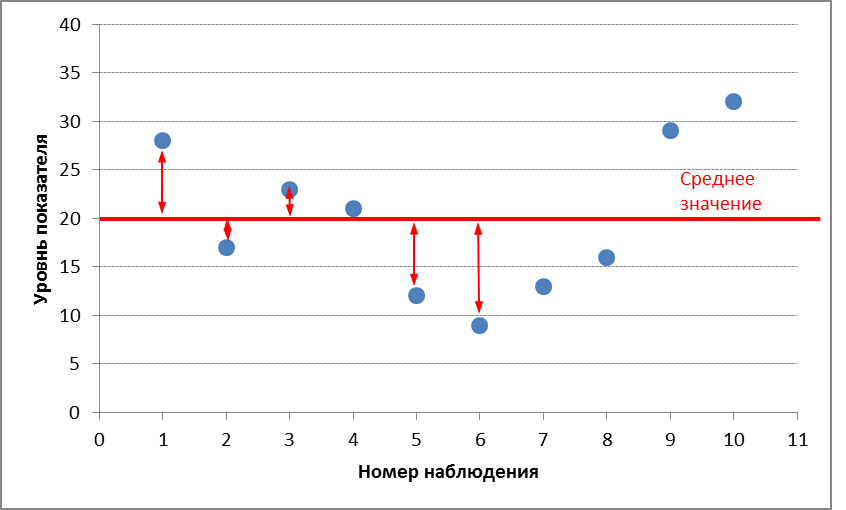
Отклонения каждого наблюдения от среднего указаны маленькими стрелочками. Именно они берутся по модулю и суммируются. Потом все делится на количество значений.
