
- •1.Что такое Всеобщее управление качеством?
- •2. История развития систем управления качеством
- •3.Основные принципы tqm.
- •4.Показатели качества продукции
- •5. Петля качества.
- •6.Цикл Деминга
- •Этапы жизненного цикла продукта и правило 10-кратных затрат
- •Три основных пути конкурентной борьбы.
- •11.Имидж компании, айсберговый эффект
- •12.Теория вариаций
- •13.Понятие размаха вариации.
- •14.Понятие среднего линейного отклонения.
- •15.Статистические методы контроля качества
- •16.Нормальный закон распределения.
- •17.Функция Лапласа
- •18.Правило трех сигм
- •19.Контрольный листок
- •20.Гистограмма
- •21.Диаграмма разброса
- •22.Диаграмма Парето.
- •23.Расслаивание (стратефикация).
- •24.Диаграмма Исикавы
- •Контрольная карта
- •Семь инструментов управления качеством
- •27.«Мозговая атака» («штурм, осада»)
- •28. Диаграмма сродства
- •29. Диаграмма связей
- •30.Древовидная диаграмма
- •31.Матричная диаграмма (таблица качества)
- •32. Стрелочная диаграмма
- •33.Процессный подход согласно стандартов исо 9000
- •34.Кружки качества.
- •35.Qfd (технология развертывания функций качества)
- •36.Профиль качества
- •37.Дом качества
- •38.Структура фаз в методе сфк
- •39.Типы улучшения качества «Кайрио» и «Кайзен»
- •40.Управление процессом по Джурану
- •41.Функции менеджмента качества
17.Функция Лапласа
Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид
где а и s—некоторые постоянные, называемые параметрами нормального распределения.
Функция распределения F(x) в рассматриваемом случае принимает вид

Использование формул f(x) и F(x) для практических расчетов затруднительно. Но решение задач по этим формулам можно упростить, если от нормального распределения с произвольными параметрами а и s перейти к нормальному распределению с параметрами а=0, s = 1.
Функция плотности нормального распределения f(x) с параметрами а=0, s =1 называется плотностью стандартной нормальной случайной величины и ее график имеет вид:
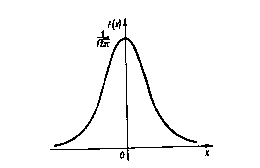
Функция плотности и интегральная функция стандартной нормальной случайной величины(СВ) будут иметь вид:

Для
вычисления вероятности попадания СВ в
интервал (a,
b)
воспользуемся функцией Лапласа:
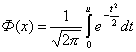
Перейдем к стандартной нормальной случайной величине
![]()
Тогда
![]()
Значения функции Ф(u) необходимо взять из таблицы приложений "Таблица значений функции Ф(х)" .
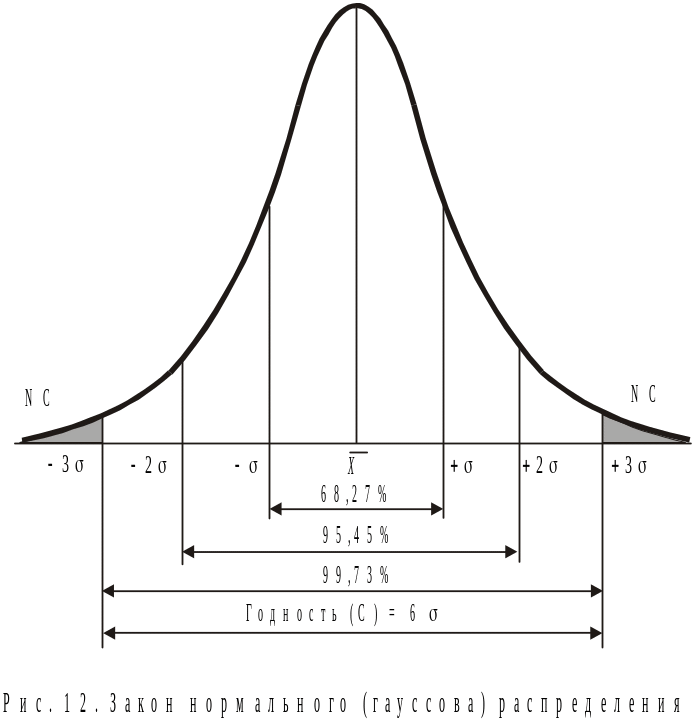
18.Правило трех сигм
![]() от
своего математического ожидания по
абсолютной величине не превысит
от
своего математического ожидания по
абсолютной величине не превысит
![]() .
.
Воспользуемся
формулой для нахождения вероятности
заданного отклонения, в которую в
качестве
![]() подставим
:
подставим
:
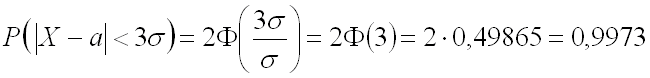 .Таким
образом, вероятность того, что отклонение
случайной величины
по
абсолютной величине будет меньше
утроенного среднего квадратического
отклонения, равна 0,9973.
Другими словами,
вероятность того, что абсолютная величина
отклонения превысит
,
составляет всего 0,0027. Такое событие,
исходя их принципа невозможности
маловероятных событий, можно считать
практически невозможным.
Вывод
(правило трех сигм):
если случайная величина распределена
нормально, то абсолютная величина ее
отклонения от математического ожидания
не превосходит утроенного среднего
квадратического отклонения.
.Таким
образом, вероятность того, что отклонение
случайной величины
по
абсолютной величине будет меньше
утроенного среднего квадратического
отклонения, равна 0,9973.
Другими словами,
вероятность того, что абсолютная величина
отклонения превысит
,
составляет всего 0,0027. Такое событие,
исходя их принципа невозможности
маловероятных событий, можно считать
практически невозможным.
Вывод
(правило трех сигм):
если случайная величина распределена
нормально, то абсолютная величина ее
отклонения от математического ожидания
не превосходит утроенного среднего
квадратического отклонения.
т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.
Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм:
19.Контрольный листок
Какая бы задача не стояла перед системой, объединяющей последовательность применения статистических методов, всегда начинают со сбора исходных данных, на базе которых затем применяют тот или иной инструмент.
Контрольный листок (или лист) — это инструмент для сбора данных и автоматического их упорядочения для облегчения дальнейшего использования собранной информации.
Обычно контрольный листок представляет собой бумажный бланк, на котором заранее напечатаны контролируемые параметры, согласно которым можно заносить в листок данные с помощью пометок или простых символов. Он позволяет автоматически упорядочить данные без их последующего переписывания. Таким образом, контрольный листок — хорошее средство регистрации данных.
Число различных контрольных листков исчисляется сотнями, и в принципе для каждой конкретной цели может быть разработан свой листок. Но принцип их оформления остается неизменным. Например, график температуры больного — один из возможных типов контрольных листков. В качестве другого примера можно привести контрольный листок, применяемый для фиксирования отказавших деталей в телевизорах (см. рисунок 3.2.).
Рис. Контрольный листок.
Дата_______ Смена____ Цех________ Бригада____ Изделие______
Границы интервала |
Группа данных |
Кол–во |
30,011-30,020 |
/ / / / |
4 |
30,021-30,030 |
|
13 |
30,031-30,040 |
|
34 |
30,041-30,050 |
|
33 |
30,051-30,060 |
|
12 |
30,061-30,070 |
/ / / / |
4 |
Итого |
100 |
|
Объем партии ________ Контролер_____________
При составлении контрольных листков следует обратить внимание на то, чтобы было указано, кто, на каком этапе процесса и в течение какого времен собирал данные, а также чтобы форма листка была простой и понятной без дополнительных пояснений. Важно и то, чтобы все данные добросовестно фиксировались, и собранная в контрольном листке информация могла быть использована для анализа процесса.
