15.Статистические методы контроля качества

Различаются две области применения статистических методов в произ­водстве (рис.):

-при регулировании хода технологического процесса с целью удержания его в заданных рамках (левая часть схемы);

-при приемке изготовленной продукции (правая часть схемы).

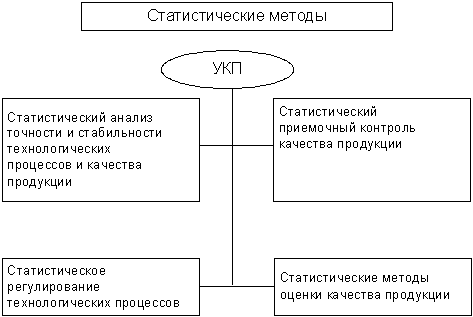
рис. Области применения статистических методов управления

качеством продукции

Для контроля технологических процессов решаются задачи статисти­ческого анализа точности и стабильности технологических процессов и их статистического регулирования. При этом за эталон принимаются допуски на контролируемые параметры, заданные в технологической документации, и задача заключается в жёстком удержании этих параметров в установленных преде­лах. Может быть поставлена также задача поиска новых режимов выполнения операций с целью повышения качества конечного производства.

Прежде чем браться за применение статистических методов в производ­ственном процессе, необходимо четко представлять цель применения этих методов и выгоду производства от их применения. Очень редко данные используются для заключения о качестве в том виде, в каком они были получены. Обычно для анализа данных используются семь, так называемых, статистических методов или инструментов контроля качества: контрольный листок, гистограмма, диаграмма разброса, диаграмма Парето, стратификация, (расслоение) диаграмма Исикавы (причинно-следственная диаграмма), контрольная карта.

16.Нормальный закон распределения.

Одним из наиболее часто встречающихся распределений является нормальное распределение. Оно играет большую роль в теории вероятностей и занимает среди других распределений особое положение.

Определение: Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид

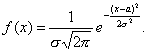
Параметр а- есть математическое ожидание случайной величины, имеющей нормальное распределение, s - среднее квадратическое отклонение, тогда дисперсия равна

Выясним геометрический смысл параметров распределения а и s. Для этого исследуем поведение функции f(x). График функции f(x) называется нормальной кривой.

Рассмотрим свойства функции f(x):

1. Функция f{x) имеет в точке х = a максимум, равный

2. График функции f(x) симметричен относительно прямой х = а.

Как видно из рисунка, нормальная кривая имеет колоколообразную форму. Эта

форма является отличительной чертой нормального распределения. Иногда нормальную кривую называют кривой Гаусса.

При изменении параметра а форма нормальной кривой не изменяется. В этом случае, если математическое ожидание (параметр а) уменьшилось или увеличилось, график нормальной кривой сдвигается влево или вправо .

При изменении параметра s изменяется форма нормальной кривой. Если этот параметр увеличивается, то максимальное значение функции f(x) убывает, и наоборот. Так как площадь, ограниченная кривой распределения и осью Ох, должна быть постоянной и равной 1, то с увеличением параметра кривая приближается к оси Ох и растягивается вдоль нее, а с уменьшением s кривая стягивается к прямой х=а .