3. Сложение чисел в простых кодах

Следует различать процедуры сложения в простых и модифицированных кодах.

В простых кодах для кодирования знака используется один старший разряд кода.

В модифицированных кодах для кодирования знака используется два разряда кода.

Ниже, в этом разделе рассматриваются особенности сложения в простых дополнительных и обратных кодах, а затем в разделе 4 сложение в модифицированных кодах.

3.1. Процедура сложения чисел в простых дополнительных кодах (ПДК)

Процедура1. Основные правила сложения в простых дополнительных кодах:

1. положительные операнды участвуют в сложении в прямых кодах;

2. отрицательные операнды должны быть преобразованы в дополнительные коды и, в таком виде – суммироваться;

3. знаковый разряд слагаемых участвует в операции наравне с числовыми разрядами;

4. перенос из знакового разряда, который может возникнуть при сложении, должен быть игнорирован (отброшен);

5. при суммировании операндов одного знака возможно отрицательное или положительное переполнение;

6. при сложении может формироваться либо положительная, либо отрицательная сумма. При этом:

6.1 если сумма – положительное число, а переполнение отсутствует, то она содержит “0” в знаковом разряде и представлена в прямом коде.

6.2 если сумма – отрицательна, то результат суммирования содержит единицу в знаковом разряде, а сумма представлена в дополнительном коде;

7. при использовании дополнительных кодов возможен случай т.н. особого переполнения (особый случай переполнения).

Далее проводится анализ различных случаев сложения (Процедура 1) в дополнительных простых кодах чисел, представленных в форматах дробных и целых чисел. Таблица 1, строится исходя из того, что на результаты сложения влияют

1. знаки слагаемых;

2. величины модулей слагаемых и их соотношение.

Учитывается то, что при сложении возможно переполнение результата, определяются признаки таких ситуаций. Выделены по перечисленным признакам девять случаев, которые могут иметь место при сложении. В последующий разделах каждый случай проанализирован с точки зрения возможности его возникновения, особенностей получаемых результатов и последствий.

3.1.1. Сложение дробных и целых положительных чисел без переполнения. (Случай 1)

3.1.1.1 Дробные числа. Пусть складываются два положительных слагаемых представленных в форме дробных чисел. Пусть также (A+B)<1.

Очевидно, что сумма в этом случае – число, представимое в заданной разрядной сетке т.е. переполнение в этом случае возникать не должно. Слагаемые представляются в прямых кодах, а сумма также должна быть сформирована прямом коде и иметь признаки положительного числа.

А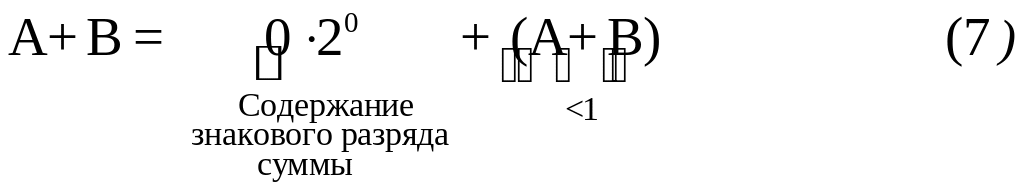 налитически эти допущения приводят к зависимости

Соотношения (7) интерпретируется следующим образом. Вследствие ограничения (А+В)<1 при сложении отсутствует перенос CY из старшего разряда модуля суммы в знаковый разряд. Такой перенос мог бы повлиять на значение знака суммы. Тогда, содержимое знакового разряда результата определяется суммой S_A+S_B+ CY =0*2⁰+0*2⁰+0=0. Таким образом, в отсутствии переноса, сумма – положительное число, представленное в прямом коде с нулевым знаковым разрядом, а переполнение отсутствует.

3.1.1.2 Целые числа. Пусть складываются два положительных слагаемых представленных в форме целых чисел. Пусть также (A+B)<2^n-1. Сложение выполняется в прямых кодах. Очевидно, что сумма в этом случае должна быть положительным числом, переполнения возникать не должно, а сумма должна быть сформирована прямом коде.

Аналитически этот случай описывается как

Таблица 2 – Случаи сложения дробных и целых чисел в простых дополнительных кодах

Знаки слагаемых	Знак		Соотношение величин модулей слагаемых	Возможность переполнения	Случай	Условия наличия/отсутствия переполнения	Знак суммы, как признак наличия/отсутствия переполнения
	A	B
Одинаковые	+	+	несущественно	возможно положительное переполнение	1, переполн. нет, сумма положит.	(A+B)<1 –для дроби (A+B)<2n-1 –для целого	“+“, совпадает со знаками слагаемых
					2, пол. переполнение	(A+B) 1 – для дроби (A+B) 2n-1 –для целого	“–“, противоположен знакам слагаемых
	–	–	несущественно	возможно отрицательное переполнение	3, переполн. нет, сумма отрицат.	|A+B|<1 –для дроби |A+B|<2n-1 –для целого	“–“, совпадает со знаками слагаемых
					4, отр. переполнение	|A+B|1 – для дроби |A+B|2n-1 – для целого	“+“, противоположен знакам слагаемых
	–	–	|A|+B|=1 –для дроби |A|+|B|=2n-1 – для целого	особый случай переполнения	5, особый случай переполнения	|A|+|B|–1= 0 –для дроби |A|+|B|–2n-1= 0 – для целого	“–“ , совпадает со знаками слагаемых
Разные	+	–	|A| > |B|	переполнение невозможно	6, сумма положит.	Переполнение невозможно, а соотношение модулей слагаемых определяет знак суммы	“+”
	+	–	|A| < |B|		7, отриц.		“–“
	–	+	|A| > |B|		8, отриц.		“–“
	–	+	|A| < |B|		9, сумма положит.		“+”

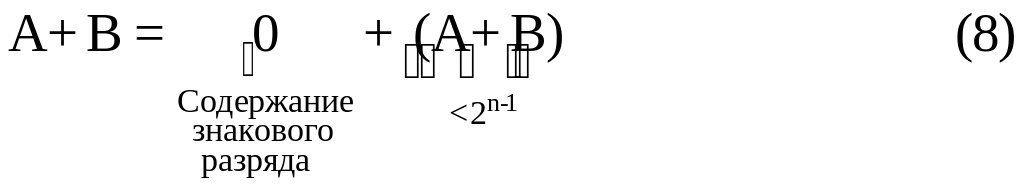Как и для дробных чисел, вследствие ограничения (А+В)<2^n-1, отсутствует перенос CY в знаковый разряд из старшего разряда модуля числа. Поэтому, содержимое знакового разряда определяется суммой S_A+S_B+ CY =0+0+0=0. Таким образом, сумма – положительное число, представляемое в разрядной сетке и сформированное в соответствующем прямом коде.

Пример 1 Сложение дробных и целых положительных чисел без переполнения (Случай 1)
Выполнить в ПДК сложение дробных А,В и целых X,Y положительных операндов.
	Дробные слагаемые равны	Целые слагаемые равны
	А= 0.742187510=0.10111112; В= 0,187510 = 0.00110002,	X= 3710 = 0 01001012; Y= 2410 = 0 00110002.
Предварительное решение. При заданных значениях слагаемых, суммы (А+В) и (X+Y) должна быть равны, соответственно (А+В) =0.929687510 ®0.11101112 и (X+Y) = 6110 ®0 01111012.
Предварительные выводы. Полученные суммы не превосходят максимальных значений чисел, представимых на заданной разрядной сетке т.е 1 для дробного числа и 127 для целого. Таким образом, при заданных слагаемых переполнения возникать не должно.
Решение. Так как все слагаемые положительные числа, то они представляются непосредственно в прямых кодах.
Сложение в двоичных простых прямых кодах имеет вид:
Т аким образом, результаты – положительные суммы без переполнения, сформированные в прямом коде, что подтверждает условия (7), (8). Признаком отсутствия переполнения является знак суммы, совпадающий со знаком слагаемых.