1. Введение в системы счисления

1.1 Общие положения. Классификация систем счисления

Системой счисления называется совокупность приемов и правил для обозначения и наименования чисел.

Система счисления задает правила кодированной записи количественных эквивалентов, позволяющие для каждого числа однозначно получать его кодовую запись и по каждой кодовой записи — соответствующий ей количественный эквивалент.

Множество символов, используемых для такого представления, называют цифрами и служебными символами. Цифры это – 0,1,2,… и т.п. К служебным относятся необходимые для записи числа символы – запятая, плюс, минус и т.п.

В микропроцессорной технике применяются в основном системы счисления, которые получили название позиционных систем счисления .

Их “ место” во множестве известных систем счисления иллюстрируется следующей классификацией СС

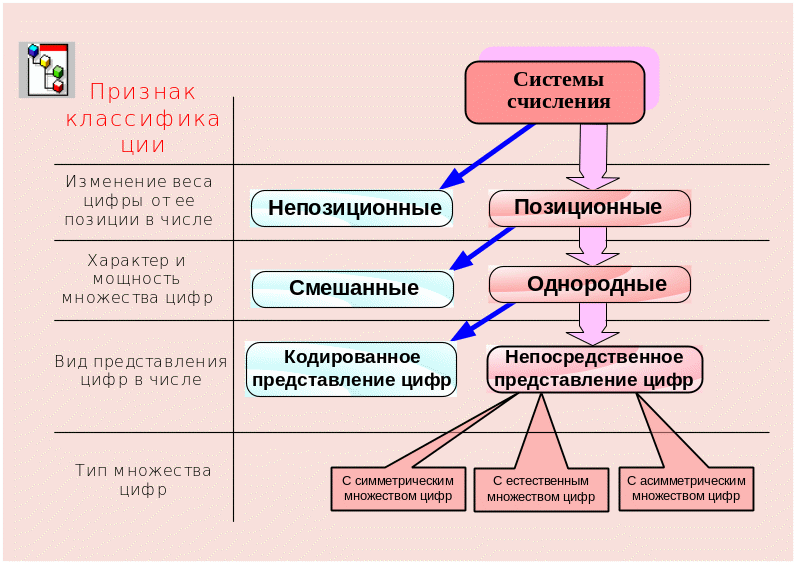
Из диаграммы следует, что кроме позиционных систем счисления существуют также непозиционные.

Непозиционные системы характеризуются сложными и громоздкими алгоритмами представления чисел и выполнения арифметических операций, поэтому они не получили значительного распространения в ЭВМ и микропроцессорной технике (МПТ).

Коротко, не углубляясь в тонкости непозиционных систем, целесообразно отметить следующее.

Цифрам в непозиционных системах соответствует некоторый числовой эквивалент, который не изменяется при изменении позиции (места) цифры в числе. Характерны в этом смысле римская и единичная (унитарная) системы. В таких системах, например десятичному числу 6, соответствуют числа VI (в римской) и 111111 (в унитарной) СС. В унитарной СС используется всего одна цифра, например – 1. Этой цифре сопоставлен количественный эквивалент, равный единице, а функцией при вычислении ко­личественного эквивалента кода числа здесь является операция сложения.

В вычислительной техники для обработки информации на всех этапах (подготовка данных, обработка, хранение и вывод результатов) используются позиционные системы.

Систему счисления называют позиционной, если одна и та же цифра может принимать различные численные значения в зависимости от местоположения (разряда) этой цифры в совокупности цифр, представляющей заданное число.

Например, вес старшей цифры 3 в десятичном числе 33 в десять раз больше веса 3 в младшем разряде, а вес старшей цифры в двоичном числе 111 – в четыре раза больше веса младшей. цифры.

Позиционные системы разделяют на однородные и смешанные. Во всех разрядах числа, представленного в однородной системе, используются цифры из одного и того же множества. Например, в обычной десятичной систе­ме во всех разрядах любого числа используются цифры из множест­ва {0,1, •••, 9}, в двоичной системе — цифры из множества {0, 1} и т. п.

В смешанных системах множества цифр различны по характеру и мощности для разных разрядов числа. Примерами смешанных систем являются, например

система для измерения углов и дуг (в разряде градусов могут быть использованы — 360 различных цифр, обозначающих градусы как координату положения, в разрядах минут и секунд –60 различных цифр),

система измерения времени, например, в секундах, минутах, часах, сутках, неделях,

система английских денежных единиц и т.п..

Если в позиционной системе для каждой цифры имеется отдельный символ, то ее называют системой с непосредственным представлением цифр. В позиционных системах с кодированным представлением цифр количество символов меньше, чем количество допустимых цифр.

В таких системах в силу “недостатка” символов каждая цифра кодируется определенной комбинацией из нескольких других символов.. Для кодирования собственных цифр используются комбинации цифр из других систем счисление. Причем должно быть установлено взаимнооднозначное соответствие между количественным эквивалентом кодируемой цифры и количественным эквивалентом кодовой комбинации.

Примером кодированной системы, используемой в ЭВМ является двоично-десятичная система – BCD ( Binary Coded Decimal). В такой системе каждая десятичная цифра представляется двоичной комбинацией из четырех цифр двоичной системы счисления – тетрадой.

Преимущественное распространение в ЭВМ и микропроцессорной технике (МПТ) получили позиционные однородные системы счисления. Причем, используются как системы с непосредственным представлением чисел, так и кодированные СС.

Всякая позиционная система задается тремя компонентами (А, , F). Здесь А— множество цифр системы; — функция, определяющая для цифр в каждом разряде их количественный эквивалент; F — функция, определяющая по количественным эквивалентам в записи числа количественный эквивалент самого числа.

Если в системе с основанием q множество цифр состоит из элементов 0, 1, ... ..., q - 1, то система имеет естественное множество цифр (естественная система счисления).

Если q = m + k +1, а множество цифр делится на два подмножества —

{–s, –s+ 1, –s+2, ..., -1} и {0, 1, 2, ..., k}, то

если s = k то система имеет симметрическое множество цифр,

если k > s или s > k , то имеет место асимметрическое соответствие в положительную или отрицательную сторону множества цифр.

Системы с такими свойствами называются соответственно – симметрической и асимметрической.

По виду функции  системы классифицируются следующим образом.

Если для любых цифр a_i из множества A имеет место соотношение (a_i,j)=q^j .(a_i,0), то система имеет основание q.

Если значение функции (a_i,j)=p_j .(a_i,0) и p_j не совпадает при различных j ,то система называется весомозначной, где – p_j веса разрядов.

Наконец, по характеру функции F системы классифицируются следующим образом.

Если в качестве этой функции используется функция сложения, то систему называют аддитивной (как в римской и в унитарной), если же используется функция умножения, систему называют мультипликативной.

В вычислительной и микропроцессорной технике используются позиционные, однородные системы счисления, с естественным кодированием. Кроме того, получили распространение и кодированные системы. Такие системы рассматриваются ниже более подробно.

Для дальнейшего анализа, целесообразно уточнить следующие термины.

Во–первых, число содержащее целую и дробную части наз. смешанным.

Во–вторых, число, состоящее только из целой части наз. целым.

В–третьих, число, состоящее только из дробной части наз. правильной дробью или дробным числом. Допустимо ( но не совсем точно) дробную часть числа называть мантиссой.

В позиционной однородной весомозначной системе с естественное множество цифр любое смешанное число X выражается в полиномиальной форме.

Целая часть числа представляется как полином вида

X_q = a_n-1*q ^n-1+a _n-2*q^n-2+ …+a_r*q^r+…+a₀ (1.1)

Дробная часть имеет вид

X_q = a_-1*q^-1+a_-2*q^-2+…+ a_-m*q^−m , (1.2)

где q − оcнование системы счисления

r − номер позиции цифры в числе r { n–1, …0,1,2,…,m}

a_r {0,1,2,…,q-1} – цифра, соответствующая r –ой позиции

n, m − длина соответственно целой и дробной части числа­

Степень q^r называется весом r-ой цифры (разряда) числа X_q

Смешанное число, представляется суммой полиномов соответственно вида (1.1) и (1.2).

Если значение q известно заранее, то числа обычно записывают в “привычной” символической форме

X = a_n-1a _n-2…a _r…a₀ , a_-1a_-2 … a_-m (1.3)

Представление числа в символической форме (1.3) наз. кодовой записью или кодом q–ичного числа.

В выражении (1.3) запятая отделяет целую часть числа от дробной, а для кодирования знака числа перед старшим разрядом используются служебные символы “ + ”, ” – “. Знак “ + ” в положительном числе может не проставляться и подразумеваться “по умолчанию”.

Одно и тоже число может быть представлено в различных системах счисления. В этом случае кодовые записи разных чисел в различных системах могут совпадать. Например, число 100 (сто) в десятичной системе и число 100 (четыре) в двоичной системе имеют одинаковые кодовые записи_, но существенно отличаются по числовому эквиваленту. Поэтому, в кодовой записи числа необходимо указывать используемую систему счисления. Для известных систем достаточно указать основание системы. Для этого могут быть использованы следующие способы.

Во–первых, основание системы может быть указано в виде нижнего индекса после кодовой записи числа.

Во–вторых, в конце кода числа может использоваться идентификатор, определяющий используемую систему счисления.

Таблица 1 — Способы указания используемой системы счисления в коде числа

Обозначение системы в числе	Система счисления
	Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная	Двоично–десятичная
Используемый индекс	10	2	8	16	2–10
Буквенный идентификатор	D или d	B или b	Q или q	H или h	BCD

Например, запись1011011,10101₂ означает, что для представления числа используется система счисления с основанием q=2. Равноценная запись – 1011011,10101B. Приведенные в Табл.1 аббревиатуры буквенных идентификаторов означают:

• D (decimal) для десятичной системы счисления,

• B(binary) для двоичной системы счисления,

• Q (octal) для восьмеричной системы счисления,

• H(hex) для шестнадцатеричной системы счисления,

• BCD– Binary Coded Decimal для двоично–десятичной системы.

Целесообразно выделить следующие свойства чисел, представимых в виде полиномов (1.1), (1.2).

С войство 1. Значение цифры r-го разряда для целой части числа в q раз больше значения такой же цифры в (r -1)-м разряде (r = п–1, ..., 1, 0). Например, цифра 9 во втором разряде целого десятичного числа 99 в десять раз больше ( с учетом веса) цифры 9 в первом разряде.

Свойство 2. Значение цифры j-го разряда для дробной части числа в q раз меньше значения такой же цифры в (j -1)-м разряде (j = –1, ..., –т). Например, цифра 1 во втором разряде десятичной дроби 0,11 в десять раз меньше ( с учетом веса) цифры 1 в первом разряде.

Систему счисления порождающую числа со Свойствами1,2 называют системой с естественным порядком весов. Существуют также системы с искусственным порядком весов, для которых указанное соотношение весов одинаковых цифр в соседних раз­рядах не является обязательным.

С войство 3. Максимальный модуль либо положительного, либо отрицательного смешанного (n+m)–разрядного числа, которое может быть представлен в форме (1.1) и (1.2). определяется как

X_max = q ⁿ − q ^{−m к}

Свойство 4. Минимальный модуль смешанного числа отличающегося от нуля, а также дробного числа представимого согласно (1.2), равен

X_min = q ^−m .

Свойство 5. Из свойства 3 следует, что максимальные модули целого и дробного чисел равны, соответственно

для целого числа X_max = q ⁿ − 1 ^к

для дробного числа X_max = 1 − q ^{−m к}

С войство 6. Из приведенных выражений следует, что максимальное количество чисел одного диапазона, которые можно предста­вить на (n+m) разрядах, определяется как

M=q ^n+m .

Свойство 7. Для представления N различных чисел в систе­ме с основанием q необходимо не менее

L = [log _q N]

разрядов. Здесь запись […] означает округление в сторону ближайшего большего целого, если число в скобках – дробное.

С войство 8.

Пусть целое q-значное n-разрядное число X_q состоит из b максимальных в этой системе счисления цифр. При этом: 1)b n; 2)младщая цифра последовательности имеет позиции k=0; 3) остальные n-b цифр цисла равны 0.

Тогда количественный эквивалент такого числа определяется как

и ли

Пример 1. Доказать, что 8-ми разрядное целое десятичное число X¹⁰, определенное разностью 10⁶–1 имеет числовой эквивалент 00999999d.

Решение. Степень 10⁶ –десятичное число 01000000. Тогда разность

10⁶–1 равна 0999999d.

Пример 2. Определить десятичный эквивалент 8-разрядного целого двоичного числа X₂=00111111b.

Решение. Согласно Свойству 7, при b=6 и k=0 X₂= 2⁶–1=63₁₀.

Для проверки полученного результата можно выполнить вычисление суммы полиномиального разложения, соответствующего исходному числу

2⁵+2⁴+2³+2²+2¹+2⁰=63₁₀

Д ругая проверка поясняет сущность операции вычитания 2⁶–1

Замечание 1.

Очевидно, что при в = n, то

Таким образом, Свойство 1 является частным случаем Свойства 8.

Замечание 2. Свойство 7 позволяет упростить реализацию арифметических операций.

Н апример, может быть упрощен перевод двоичных чисел соответствующих условиям Свойства 8 в десятичную систему счисления. Замена суммирования b членов полиномиального ряда вычислением разности qⁿ–1 приводит к упрощению вычислений. Причем, выигрыш в упрощении тем больше, чем длиннее последовательность.

Свойство 9.

Пусть q-значное n-разрядное целое число X_q содержит последовательность из b максимальных в этой системе счисления цифр(b n).

Младшая цифра последовательности занимает k-ую (n-1 k 0) позицию в числе, т.е.

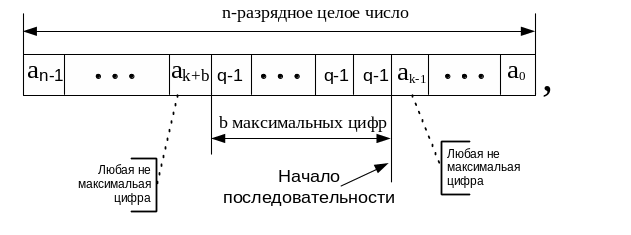
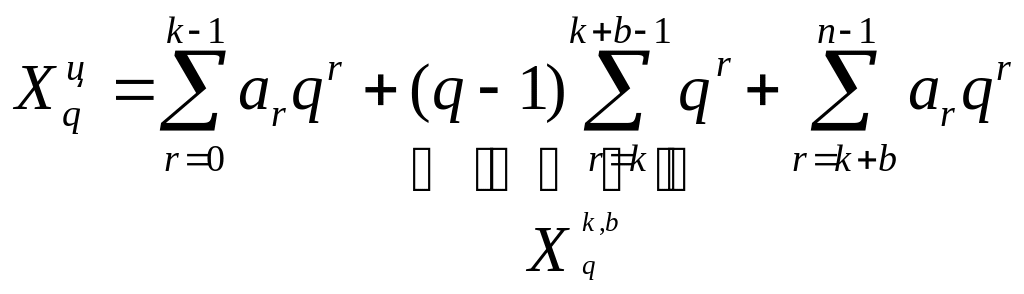
Тогда количественный эквивалент числа определяется как

а количественный эквивалент последовательности как

Пример3. Определить количественный эквивалент последовательности из 6-ти максимальных цифр в 9-ти разрядном десятичном числе

X₁₀ =9369999954D.

Согласно заданное число можно представить как 9360000000+(10⁷–10²)+0000000054.

П ри этом разность (10⁷–10²⁾ оценивает количественный эквивалент последовательности из 6-ти девяток, младшая цифра которой занимает вторую позицию в числе

Р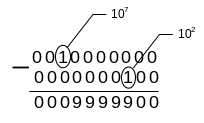 азность “в столбик” определяется как

Тогда X¹⁰ =9360000000+0009999900+0000000054=9369999954, что подтверждает справедливость Свойства 8.

Пример 4. Определить количественный эквивалент последовательности из 7-ми максимальных цифр в 12-ти разрядном двоичном числе

X₂ =100111111101b.

Согласно заданное число можно представить как 10000000000+(2⁹-2²)+000000000001.

Количественный эквивалент последовательности в десятичной системе счисления определяется путем вычисления разности (2⁹-2²). Степени равны 2⁹=512 и 2²=4, а их разность (2⁹-2²)=512 - 4=508.

Использование вычислений в “столбик” приводит к результату

В результате последующего суммирования 100000000000+000111111100+00000000001=100111111101b получается исходное число, что подтверждает справедливость Свойства 9.

Свойство 10. Пусть дробная часть q-значного n-разрядного числа Xq состоит из b максимальных в этой системе счисления цифр. При этом bm.

Начальные условия поясняются рисунком.

О чевидно, что

Тогда при введенных условиях Свойство 9 состоит в следующем

и ли

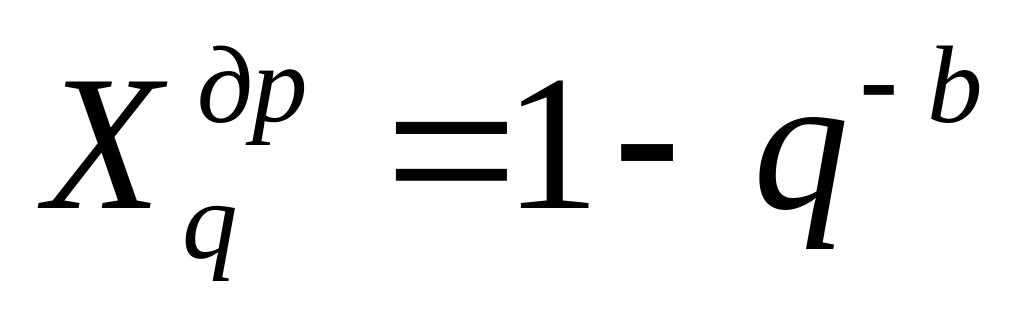
Пример5. Определить количественный эквивалент 16-ти разрядного дробного двоичного числа 0,111111100000000b, дробная часть которого состоит из 7-ми максимальных цифр.

Решение. Согласно ( ) заданное число X2 =0,111111100000000b, представляется как X₂= 1– 2^–7=(128-1)/128=0,9921875.

Пример 6. Подтвердить, что разность 1– 2^–9 задает двоичное дробное число 0,11111111100.

Р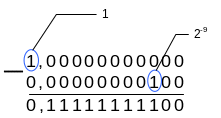 ешение. 2^–9=0,000000001. Вычитание в “столбик” приводит к результату

Т аким образом, разность 1– 2^–9 = 0,11111111100. Это подтверждает условие примера.

Свойство 11.

Пусть q-значное m-разрядное дробное число Xq содержит последовательность из b максимальных в этой системе счисления цифр(bm).

Старшая цифра последовательности занимает k-ую позицию в числе. Условия, для которых определено Свойство 11 иллюстрируются рисунком

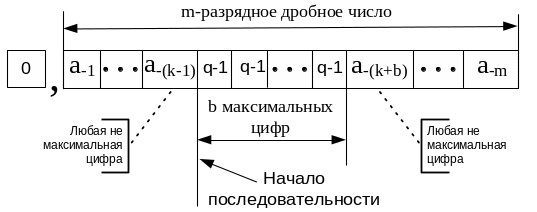
Очевидно, что справедливо представление заданного числа в виде

а далее

К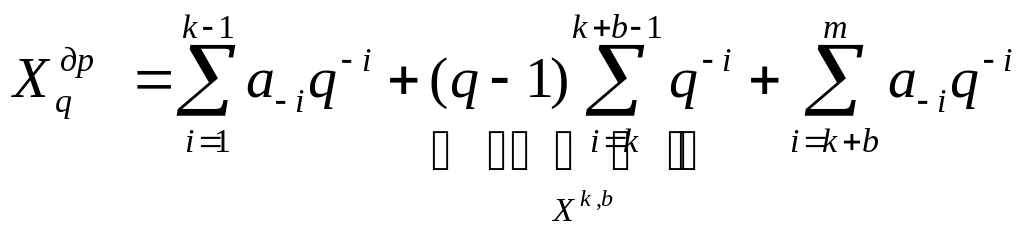 оличественный эквивалент X^k,b задается соотношением

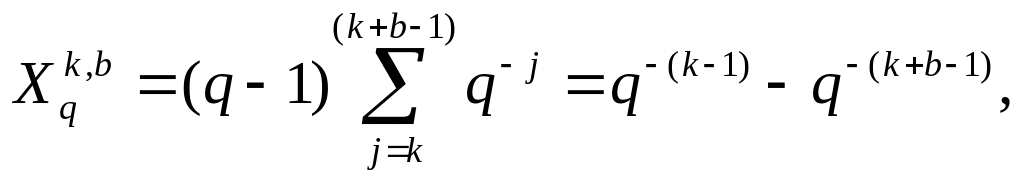
Таким образом, свойство 11 состоит в следующем:

Количественный эквивалент последовательности из b максимальных цифр, старшая из которых занимает k-ую позицию в дробном q-ичном числе определяется разностью степеней

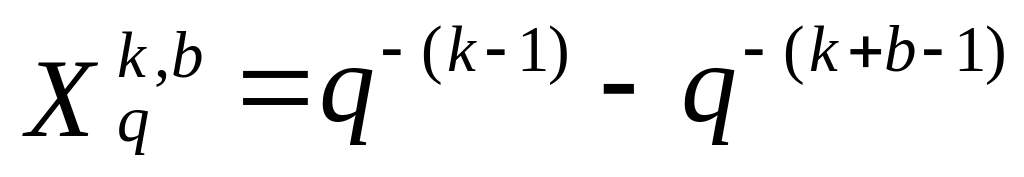
Соотношение можно проверить, задавшись, например, параметрами k=2, b=5.

Последовательность в соответствующем числе начинается со второй позиции и включает 5 цифр.

Т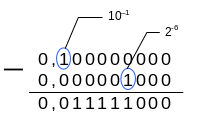 огда её количественный эквивалент определяется разностью 2^–1–2^–6, т.е.

Количественный эквивалент двоичной последовательности X^2,5, подсчитанный через разность 2^–1–2^–6 равен 0,484375.

Вычисление через полиномиальное разложение приводит к аналогичному результату 2^-2+2^-3+2^-4+2^-5+2^-6=0,484375.

Пример иллюстрирует упрощение вычислений при использовании Свойства 11.

Г лавным преимуществом позиционных систем счисления по сравнению с непозиционными является удобство представления чисел и простота выполнения арифметических операций. Недостаток по­зиционных систем — невозможность выполнения арифметических операций как поразрядных, т.е. операций не формирующих межразрядные переносы или заемы.