1.2 Системы счисления, используемые в мпт

В микропроцессорной технике применяются следующие системы счисления.

Десятичная. Привычная “школьная” система с основанием q=10, в которой используется десять цифр a_r Î{0,1,2,…,9}. В этой системе могут представляться исходные данные, решаются контрольные примеры и выводятся на различные носители и средства визуального отображения полученные результаты.

Двоичная. Основание такой системы q=2. Используется две цифры a_rÎ{0,1}.

В двоичной системе счисления смешанное число X₂ выражается в следующем виде.

Целая часть числа представляется двоичным полином вида

X₂ = (a_n-1*10 ^n-1+…+a_2*10¹⁰ +a_1*10⁰¹+a₀)₂ (1.4)

Дробная часть имеет вид

X₂ =(a_-1*10^-001+a_-2*10^-010+…+a_-m*10^−m)₂ , (1.5)

где a_r {0,1} - используемые на r – ой позиции двоичные цифры

n, m − длины соответственно целой и дробной части числа, выраженные двоичными числами

Такая система естественно отражает состояния элементов дискретных ключевых схем, являющихся базой микропроцессорной схемотехники, поэтому на этой системе основываются аналитические бинарные модели дискретных устройств. Двоичная система также применяется для непосредственного ввода данных в МПТ, вывода полученных результатов. Однако, из Свойства 7 следует недостаток двоичной системы: для представления чисел в систе­ме с основанием 2 необходимо больше разрядов, чем, в других систем с непосредственным представлением чисел.

Шестнадцатеричная. Известная система с основанием q=16, в которой используется шестнадцать цифр a_r Î{0,1,2,…,9, A,B,C,D,E,F}. В качестве цифр, превышающих по значению 9, используются прописные буквы латинского алфавита.

В шестнадцатеричной системе счисления смешанное число X₁₆ вы­ражается в следующем виде.

Целая часть числа полином вида

X₁₆ = (a_n-1*10 ^n-1+…+a_A*10^A +… +a₀)₁₆ (1.6)

Дробная часть представляется как

X₁₆ =(a_-1*10^-1+…+a_-A*10^-A+…+a_-m*10^−m)₁₆ ,(1.7)

где

a_r Î{0,1,2,…,9, A,B,C,D,E,F} – используемые шестнадцатеричные цифры

n, m − длины соответственно целой и дробной части числа, выраженные шестнадцатеричными числами

Шестнадцатеричная система в силу компактности записи числа удобна для задания данных и символического отображения внутренних состояний функциональных частей МПТ. Она обеспечивает компактный вывод данных и результатов на средства визуального отображения – электролюминисцентные индикаторы, в поля ввода–вывода экранных форм и т.п.

Это преимущество шестнадцатеричных систем счисления иллюстрируется Рисунком 1, на котором приведены символические экраны для вывода десятичного числа X =60658 в шестнадцатеричной СС (X=ECF2h) и двоичной системе счисления X= 1110110011110010B.

Восьмеричная. Система с основанием q=8, в которой используется восемь цифр a_r Î{0,1,2,…6,7}.

В восьмеричной системе счисления смешанное число X₈ выражается в следующем виде.

Целая часть числа представляется как полином вида

X₈ = (a_n-1*10 ^n-1+…+a_7*10⁰⁷ +… +a₀)₈ (1.8)

Дробная часть имеет вид

X₈ =(a_-1*10^-1+…+a_-7*10^-07+…+a_-m*10^−m)₈ ,(1.9)

где a_r Î{0,1,2,…,7} – используемые восьмеричные цифры

n, m − длины соответственно целой и дробной части числа, выраженные восьмеричными числами

Двоично-десятичная система счисления (BCD ( Binary Coded Decimal)). Относится к двоично–кодируемым позиционным системам.

Основанием системы является десятичное число 10, а для кодирования десятичных цифр используется десять двоичных четырехразрядных комбинаций (тетрад). Каждая комбинация однозначно соответствует десятичной цифре в десятичном числе.

Известно, что число двоичных четырехразрядных комбинаций превышает число цифр десятичной системы счисления. Действительно – 2⁴ 10.

Вследствие этого возникает дополнительная проблема выбора оптимального по определенным критериям соответствия между десятичными цифрой и двоичными тетрадами (кодирование).

Н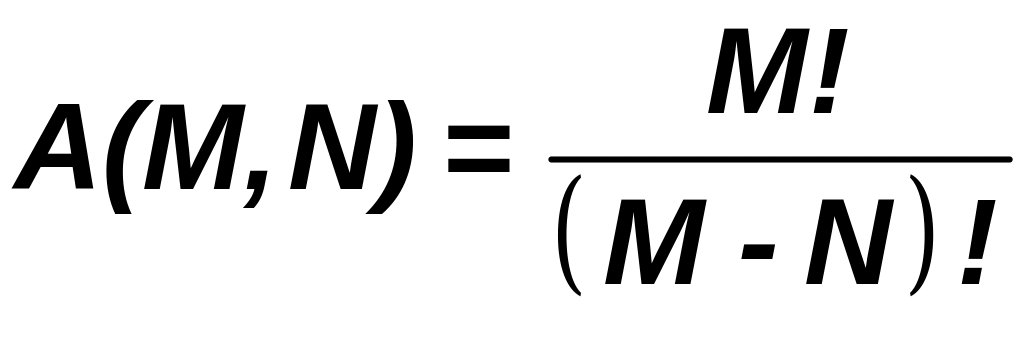 етрудно показать, что число различных вариантов кодирования определяется как число размещений с перестановками из шестнадцати элементов на десяти местах. Такое число A(M,N) может быт подсчитано как

Подсчеты показывают, что число кодов около 6 млн.(!). Актуальность решения задачи выбора кода усугубляются тем, что тип отображения цифра → тетрада порождает код с уникальными свойствами. Пригодность и эффективность конкретного кода для машинных расчетов – различна.

Поэтому при выборе кода желательно, чтобы были учтены некоторые ограничения.

Известны пять основных требований (критериев), которые сформулированы Рутисхаузером.

1. Единственность. Необходимо однозначное соответствие цифр и тетрад. Если это требование не выполнено, то невозможно кодирование и декодирование чисел.

2. Упорядоченность. Большим десятичным цифрам должны соответствовать большие (по количественному эквиваленту) тетрады.

Выполнение этого требования необходимо при сравнении кодированных чисел.

3. Четность. Четным десятичным цифрам должны соответствовать четные тетрады (тетрады, у которых в крайнем правой разряде стоит нуль), а нечетным цифрам — нечетные тетрады.

4. Дополнительность. Если цифры десятичной системы таковы, что сумма их равна девяти, то им должны сопоставляться тетрады, которые взаимно инвертированы, т. е. получаются друг из друга заменой единиц на нули, а нулей на единицы. Выполнение этого требования необходимо для того, чтобы ввести в двоично-десятичной системе дополнительный или обратный код.

5. Весомозначность. Должны существовать четыре веса р_0, р₁, р₂, р₃ таких, что если десятичной цифре х сопоставлена тетрада (a₃ a₂ a₁a₀), то имеет место равенство

х= a₃р₃ + a₂ р₂+a₁р₁ + a₀р₀

К весомозначности приводит, например, следующий способ кодирования: каждая десятичная цифра кодируется ее записью в двоичной системе с использованием полинома вида (1.4) .

В этом случае цифра 5 будет закодирована тетрадой 0101, цифра 6 –тетрадой 0110 и т.д. Такой способ кодирования называется кодом прямого замещения с весами (8, 4, 2, 1).

Кодирование, удовлетворяющее всем пяти требованиям, называется совершенным.

Код прямого замещения не является совершенным. Действтельно, он удовлетворяет всем требованиям Рутисхаузера, кроме четвертого. Нарушение этого требования не позволяет вводить дополнительный или обратный код, что в свою очередь не позволяет заменить вычитание операцией сложения.

Для выполнения свойства дополнительности можно кодировать десятичную цифру х тетрадой Т(х), равной х + 3. Полученный код называется кодом с избытком 3, или кодом Штибитца.

Однако, кодирование с избытком 3, как и код прямого замещения, не является совершенным т.к.не обладает свойством весомозначности

Коротко останавливаясь на свойствах возможных вариантов кодирования целесообразно выполнить следующий анализ.

Для кодирования единицы необходимо, чтобы один из весов был равен 1. Если считать, что р₀ = 1, то необходимо чтобы р₃ + р₂+ р₁ = 8. Возможны следующие комбинации весов (р₃ , р₂, р₁) с точностью до их переста­новки:

(6,1,1), (5,2,1), (4,2,2), (3,2,3), (4,1,3).

Соответсвующие варианты кодирования (комбинации весов) сведены в таблицу.

Таблица 2 – Варианты двоично–десятичного кодирования

Кодируемая десятичная цифра x	Значение тетрады Т(х)в системе счисления
	(8,4,2,1)	(6,1,1,1)	(5,2,1,1 )	(3,3,2,1)	(4,3,1,1)	(2,4,2,1)	х + 3
0	0000	0000	0000	0000	0000	0000	0011
1	0001	0001	0001	0001	0001	0001	0100
2	0010	0011	0100	0010	0010	0010	0101
3	0011	0111	0101	0011	0100	0011	0110
4	0100	—	0111	0101	0110	0100	0111
5	0101	—	1000	1010	1001	1011	1000
6	0110	1000	1010	1100	1011	1100	1001
7	0111	1001	1011	1101	1100	1101	1010
8	1000	1011	1110	1110	1110	1110	1011
9	1001	1111	1111	1111	1111	1111	1100

Данные таблицы позволяют сделать следующие выводы.

В системе с весами (8,4,2, 1) отсутствует свойство дополнительности.

Для случая (6,1, 1,1) нарушается первое требование Рутисхаузера: для цифр 4 и 5, т.е. отсутствуют соответствующие тетрады.

В системе с весами (5, 2, 1, 1) не выполняется требование четности для цифр 4 и 5.

В системе с весами (3, 3, 2, 1) не выполняется требование четности для цифр 4 и 5.

В системе с весами (4, 3, 1, 1) не выполняется требование четности для цифр 2, 3, 6, 7.

Кодирование с избытком 3, как и код прямого замещения, не является совершенным т.к. не обладает свойством весомозначности

В системе с весами (2, 4, 2, 1) все пять требований выполнены, соответствующая арифметика является совершенной и называется в честь авторов — арифметикой Айкена—Эмери.

Двоично–десятичные системы эффективны при решении задач обработки больших массивов десятичных чисел. Например, при обработке массивов десятичных параметров (экономические задачи). В этом случае, за счет упрощения процедур перевода десятичных чисел в BCD–систему и обратно, может быть достигнуто повышение производительности вычислительного средства.

В таблице 3 приведены в качестве примера некоторые числа . представленные в рассмотренных системах.

Таблица 3 – Примеры кодирования чисел в машинных системах счисления

Число в десятичной СС	Число в двоичной СС	Число в шестнадцатеричной СС	Число в восьмеричной СС	Число в двоично–десятичной СС
				Код прямого замещения	Код Айкена—Эмери
00	0000	0	0	0000 0000	0000 0000
01	0001	1	1	0000 0001	0000 0001
02	0010	2	2	0000 0010	0000 0010
03	0011	3	3	0000 0011	0000 0011
04	0100	4	4	0000 0100	0000 0100
05	0101	5	5	0000 0101	0000 0101
06	0110	6	6	0000 0110	0000 1100
07	0111	7	7	0000 0111	0000 1101
08	1000	8	10	0000 1000	0000 1110
09	1001	9	11	0000 1001	0000 1111
10	1010	A	12	0001 0000	0001 0001
11	1011	B	13	0001 0001	0001 0001
12	1100	C	14	0001 0010	0001 0010
13	1101	D	15	0001 0011	0001 0011
14	1110	E	16	0001 0100	0001 0100
15	1111	F	17	0001 0101	0001 0101
16	10000	10	20	0001 0110	0001 1100
17	10001	11	21	0001 0111	0001 1101
0,0625	0,0001	0,1	0,04	0,0000011000100101	0,0000110000100101
0,125	0,001	0,2	0,1	0,000100100101	0,000100100101
0,25	0,01	0,4	0,2	0,00100101	0,00100101
0,375	0,011	0,6	0,3	0,001101110101	0,001111010101
0,5	0,1	0,8	0,4	0,0101	0,0101
0,625	0,101	0,A	0,5	0,011000100101	0,110000100101
0,75	0,11	0,C	0,6	0,01110101	0,11010101
Примечание – для экономии места в таблице “0” в целой части дробных BCD чисел записывается не тетрадой, а одной цифрой