1. Преобразование чисел в различные системы счисления

Для практической деятельности актуальна задача преобразования чисел представленных в одной системе счисления в другую (конвертирование). Задача состоит в представлении числа в требуемой СС с основанием q_тр , если оно задано в исходной системы СС с основанием q_исх .

Д ля преобразований могут использоватьcя методы, перечисленные в следующей диаграмме.

2.1 Метод непосредственного замещения

Алгоритм преобразования методом непосредственного замещения имеет вид.

1. Число заданное в исходной системе счисления с основанием q_исх , представляется в виде суммы полиномов (1.1) и (1.2). При этом используются цифры исходной системы.

2. Все цифры и числа, используемые в полученном полиноме заменяются их представлениями в новой СС.

3. Выполняются соответствующие операции по правилам новой СС. К таким операциям относятся – возведение в степень оснований, умножение полученных степеней на цифры и сложение полученных произведений.

4. Полученная сумма – число в новой системе счисления.

При конвертировании из двоичной в десятичную систему преобразования обычно начинают со второго этапа.

Эффективность метода непосредственного преобразования зависит от соотношения оснований исходной и требуемой систем. В основном он применяется, причем начиная со второго этапа, при преобразованиях из двоичной в десятичную систему счисления.

Особенно эффективен при “ручных” преобразованиях малоразрядных целых, реже дробных чисел.

2.2 Преобразования по схеме Горнера

.Применение схемы Горнера обеспечивает значительное ускорение процедур конвертации. Рассматриваемый метод является частным случаем метода непосредственного замещения, рассмотренного ранее. Конвертация как в методе непосредственного замещения в обеспечивается за счет замещения (этапы 1-2 алгоритма непосредственного замещения). Однако дальнейшие операции ускоряются за счет замены операций возведения в степень операциями последовательного умножения (деления) по схеме Горнера.

Алгоритм метода имеет вид

1. Число заданное в исходной системе счисления с основанием q_исх , представляется в виде суммы полиномов (1.1)и (1.2). При этом используются цифры исходной системы.

2. Все цифры и числа, используемые в полученном полиноме заменяются их представлениями в новой СС. Числами (цифрами) в новой системе счисления представляются коды цифр, оснований и степеней оснований в старой системе.

3. Дальнейшие преобразования целой и дробной части выполняются раздельно и сводятся к вычислениям по следующим схемам Горнера

3.1 для целой части

X =(… (a_n-1*q_ТР +a_n-2)* q_ТР +a_n-3) * q_ТР+a_n-4)* q_ТР +…+a₁)* q_ТР +a₀

Для вычислений требуется (n-1) умножений и сложений.

3.2 для дробной части

X =(… (a_-m/q_ТР +a _-m+1)/ q_ТР + a _-m+2)/ q_ТР+ a _-m+3)/ q_ТР +…+a_-1) / q_ТР

Для вычислений требуется m умножений и сложений.

Э тапы 1,2 могут выполняться «в уме», а вычисления начинаться с этапа 3.

Коротко останавливаясь на достоинствах метода необходимо отметить следующее. Метод хорошо формализован, поэтому удобно реализуется средствами вычислительной техники с использованием циклических алгоритмов. Недостатки связаны с необходимостью замещения кодов цифр, оснований и степеней в старой системе их эквивалентами в новой системе счисления. В основном применяется, при преобразованиях из двоичной в десятичную систему счисления.

Особенно эффективен при “ручных” преобразованиях малоразрядных целых, реже дробных чисел. Разрядность преобразуемых чисел может быть больше, чем в методе непосредственного замещения.

2.3 Метод “ цифра за цифрой”

Метод “цифра за цифрой” предусматривает последовательное получение цифр кода конвертированного числа.

При этом для целого числа, а равно для целой части смешанного числа конвертирование выполняется с использованием операции деления, а для дробного числа (дробной части смешанного числа) с использованием операции умножения. Конверсия для каждой части имеет свои особенности, поэтому соответствующие алгоритмы целесообразно рассмотреть отдельно.

Метод “ цифра за цифрой “ для целого числа (деление “ лесенкой “)

Преобразование целого числа или целой части смешанного числа. Требуется выполнить преобразование Xq → X_h. Исходное число заданое в СС с основанием q. Необходимо представить его в СС с основанием h.

Исходной целое число Xq в требуемой системе счисления с основанием h имеет вид

Xq = a_N-1*h ^N-1+a _N-2*h ^N-2+…+a_0*h⁰ (2.1)

Очевидно, что при конвертировании число разрядов для представления исходного числа в новой системе счисления может измениться. Это нашло отражение в разложении 2.1, в котором N – новая разрядность целой части искомого числа (N ≠ n).

Задача конвертирования заключается в определении неизвестных пока полиномиальных коэффициентов a_N-1, a _{N-2, … ,} a_0. Это выполняется путем деления исходного числа на основание требуемой системы счисления.

Деление Xq на h приводит к результату

(Xq):h = a_N-1*h ^N-2+a _N-2*h^N-3+ …+a₁ +(a₀):h

Если обозначить полученное частное как y₁, то результат деления можно записать как

Xq = y₁*h + a₀

Таким образом, младшая цифра искомого представления Xq в новой системе счисления − есть остаток от деления исходного числа на h. Если продолжить деление частного y₁ на h , то получается результат

( y₁):h = a_n-1*h ^n-3+a _n-2*h^n-4+ …+a₂+(a₁):h

в силу

y₁= y₂*h + a₁

остаток от второго деления есть вторая цифра исходного числа в h системе счисления.

Таким образом, последовательное деление обеспечивает последовательное получение цифр исходного числа в новой системе счисления. ( “цифра за цифрой”)

Поэтому алгоритм преобразования целого числа методом “цифра за цифрой”. может быть сформулирован в следующем виде.

Число Xq делится на q _тр по правилам деления системы с основанием q _исх до получения остатка.

Если частное от деления - не нуль, то частное становится делимым и процесс деления на q _тр продолжают.

Как только очередное частное станет равным нулю, либо станет меньше q _тр -- процесс деления на q _тр прекращается. Остаток, полученный при первом делении на q _тр, представляет цифру разряда результата с весом q⁰ в требуемой системе счисления. Остаток от второго деления представляет цифру разряда результата с весом q¹ и т. д. Последний остаток является старшей цифрой результата, имеющей вес q^n-1 .

Пример 5. Представить десятичное число 45D в двоичной системе счисления. Целесообразно применить метод “цифра за цифрой” в варианте “деление лесенкой”

Таким образом, X₁₀=45₁₀ =101101B

П роведенный аналитический анализ позволяет сделать вывод об универсальном характере метода к соотношению оснований исходной и заданной систем.

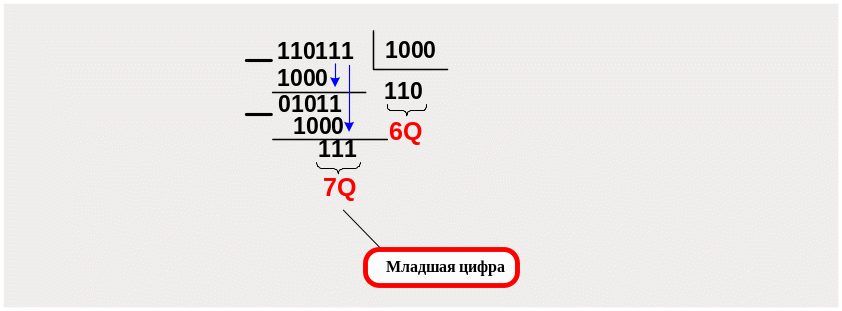
Пример 6. Преобразовать двоичное число 110111В в восьмеричную систему счисления. Формализованная запись задания 110111В → XQ.

Основание“новой” восьмеричной системы счисления − 8Q=1000В

Деление “лесенкой” выполняется по правилам двоичной (исходной) системы счисления.

Т аким образом, исходное двоичное число 110111В в восьмеричной системе счисления запишется как 67Q.

П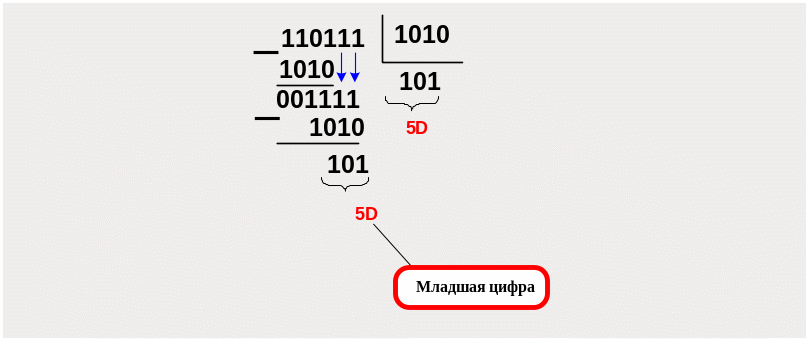 ример 7. Преобразовать двоичное число 110111В в десятичную систему счисления. Формализованная запись задания 110111В → XD.

Применяется “ деление лесенкой” целой части заданного числа на основание новой системы счисления записанное в виде двоичного целого − 10D =1010В

Таким образом, заданное числе в десятичной системе счисления представляется как 110111B = 55D.

П ример 8. . Преобразовать десятичное число 155D в шестнадцатеричную систему счисления. Формализованная запись задания 155D → XH.

П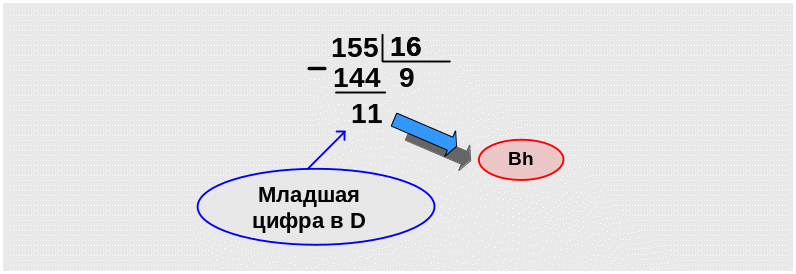 рименяется “ деление лесенкой” целой части заданного числа на основание новой системы счисления записанное в виде десятичного целого − 10H =16D.

Заданное число 155D в шестнадцатеричной системе счисления представляется как 9BH.

П ример 9. . Преобразовать десятичное число 155D в восьмеричную систему счисления. Формализованная запись задания 155D → XQ.

П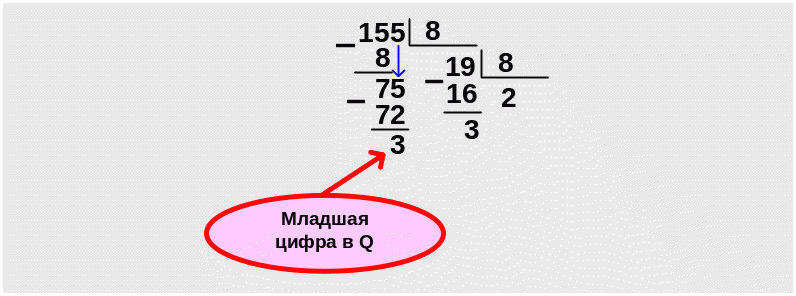 рименяется “ деление лесенкой заданного числа на основание новой системы счисления − 10Q =8D.

Заданное число 155D в восьмеричной системе счисления запишется как 233Q.

Целесообразно отметить несколько свойств и особенностей алгоритма “деление лесенкой”.

Первое. Алгоритм теоретически обеспечивает преобразование из системы с любым основанием в заданную систему с любым основанием. Это свойство иллюстрируется примерами 3-9.

Второе. Преобразования необходимо выполнять по правилам исходной системы счисления, что не всегда удобно и привычно.

Третье. Область преимущественного использования метода для “ручных” преобразований – преобразование из десятичного представления числа в двоичное, а также в восьмеричное и в шестнадцатеричное.

Четвертое. Алгоритм хорошо формализован и, как следствие, эффективен не только для ручных преобразований, так и для реализации на ЭВМ и МПТ.

Метод “ цифра за цифрой для правильной дроби (”последовательное умножение “)

Перевод правильных дробей из системы счисления с основанием q _исх в систему с основанием q _тр осуществляется так.

Как и при конвертировании целого числа, исходное число − правильная дробь, заданная в СС с основанием q _исх. Необходимо представить ее в СС с основанием h. В требуемой системе счисления (основание – h) правильная дробь Xq является полиномом вида

Xq = a_-1*h ^-1+a_-2*h ^-2+… a_-M+1*h ^−M+1 + a_-M*h ^−M (2.2)

Очевидно, что при конвертировании число разрядов для представления исходного числа в новой системе счисления может измениться . Поэтому целесообразно вместо обозначения m, применявшегося ранее в (2.2) обозначать новую разрядность как М (.M ≠ m).

Как и ранее, задача конвертирования заключается в определении неизвестных пока полиномиальных коэффициентов a_-1, a _{-2, … ,} a_-M.

Умножение полинома (1.4) на h позволяет получить произведение вида

Xq* h = a_-1+a_-2*h ^-1+… a_-M+1*h ^−M+2 + a_-M*h ^−M+1 = a_-1+ z₁

В полученном произведении содержится в виде целой части старшая цифра числа Xq и дробная часть z₁. Если опять умножить правильную дробь z₁ на основание h, то целая часть произведения дает следующую цифру числа в новой системе счисления и т.д. Правило перевода правильных дробей в новую систему счисления методом “цифра за цифрой” (“последовательное умножение”) формулируется следующим образом.

Дробь, соответствующая числу Xq, умножается на q тр по правилам умножения в системе с основанием q исх.

В полученном произведении отделяется целая часть, которая может быть равной нулю, а дробная часть снова умножается на q тр с последующим отделением целой части.

Эти операции повторяют

1. либо до получения нулевой дробной части произведения,

2. либо до получения необходимого количества разрядов числа Xq в новой системе счисления

3. либо до достижения заданной точности преобразования.

. Старшая цифра результата перевода (то есть первая после запятой) совпадает с первой отделенной целой частью, вторая цифра результата — со второй отделенной целой частью и т. д.

Нулевая дробная часть произведения формируется лишь для небольшого числа преобразуемых чисел. Для таких чисел должен существовать конечный полином вида 1.2 в требуемой системе счисления. Преобразование такого типа иллюстрируется Примерами 10, 11.

П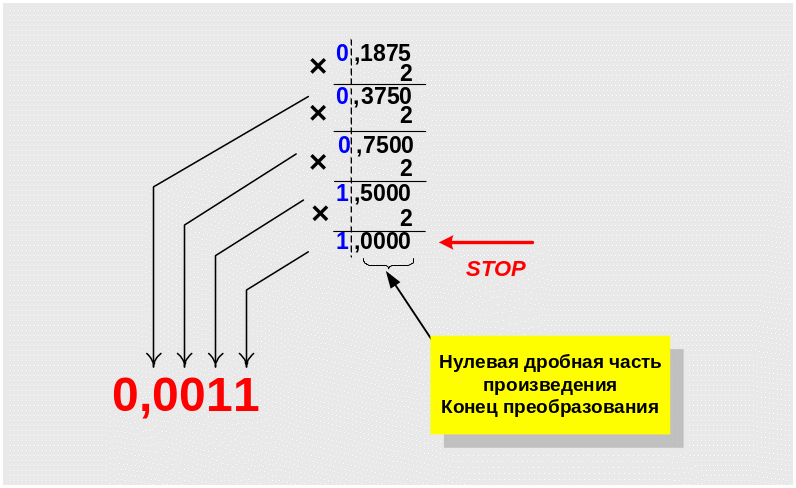 ример 10. . Преобразовать десятичное число 0,185D в двоичную систему счисления. Формализованная запись задания 0,185D → XB.

Результат преобразования конечен и имеет вид 0,185D = 0,0011B

П ример 11. Преобразовать двоичную правильную дробь XB =0, 01011В в восьмеричную систему счисления. Формализованная запись задания 0,01011В → XQ.

П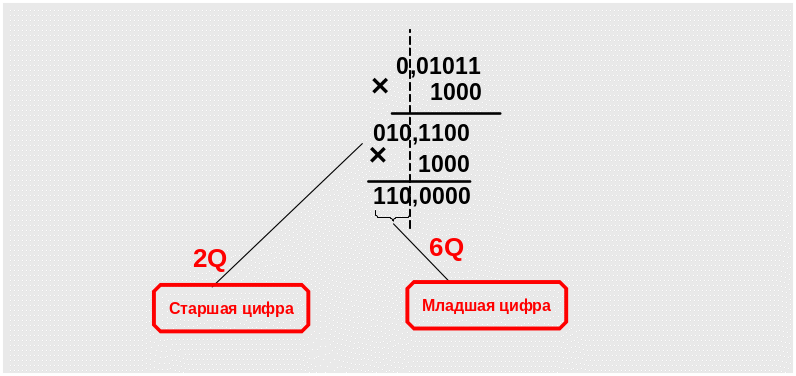 рименяется последовательное умножение дробной части двоичного числа на основание восьмеричной системы, представленное в виде двоичного целого. Преобразования выполняются по правилам двоичной системы счисления.

Таким образом, 0,01011В = 0,26Q,

Наиболее вероятны случаи либо ограничения количества разрядов числа Xq в новой системе счисления, либо достижения заданной точности преобразования.

Для вычислительных систем как правила имеет место ограничение разрядной сетки для представления числа в новой системе счисления. Эти случаи иллюстрируются примерами 12,13.

П ример 12. Преобразовать дробное двоичное число X₂= 0,01011В в десятичную систему счислении. Дополнительные требования: полученное десятичное число должно содержать не более трех разрядов для представления мантиссы. Формализованная запись задания 0,01011В → XD.

П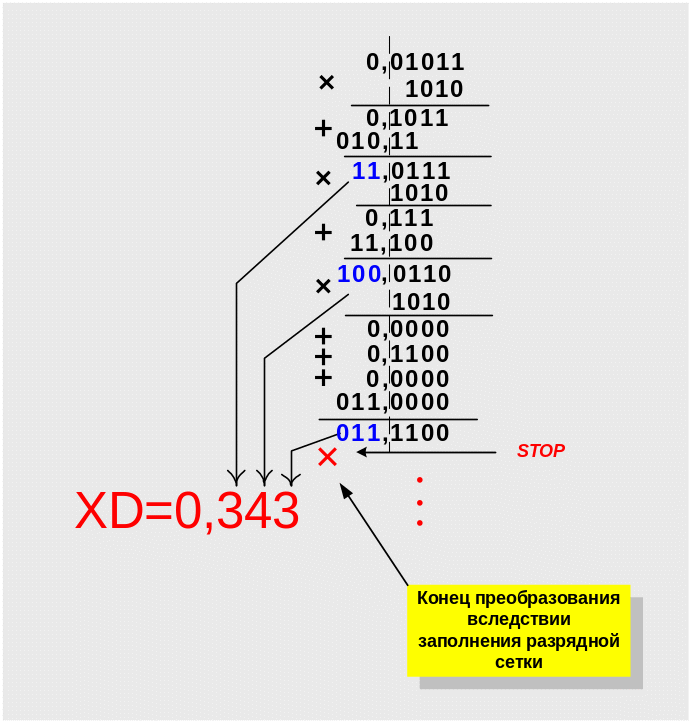 рименяется последовательное умножение дробной части двоичного числа на основание десятичной системы, представленное в виде двоичного целого. Преобразования выполняются по правилам двоичной системы счисления.

Таким образом, заданное двоичное число 0,01011B в десятичной системе счисления представляется приближенно, и равно 0,343D.

Следующий пример иллюстрирует то, что даже при бесконечной разрядной сетке преобразования могут не привести к конечному числу в новой системе счисления.

П ример 13. Преобразовать дробное десятичное число X₂= 0,1D в двоичную систему счисления. Формализованная запись задания 0,1D → XB..

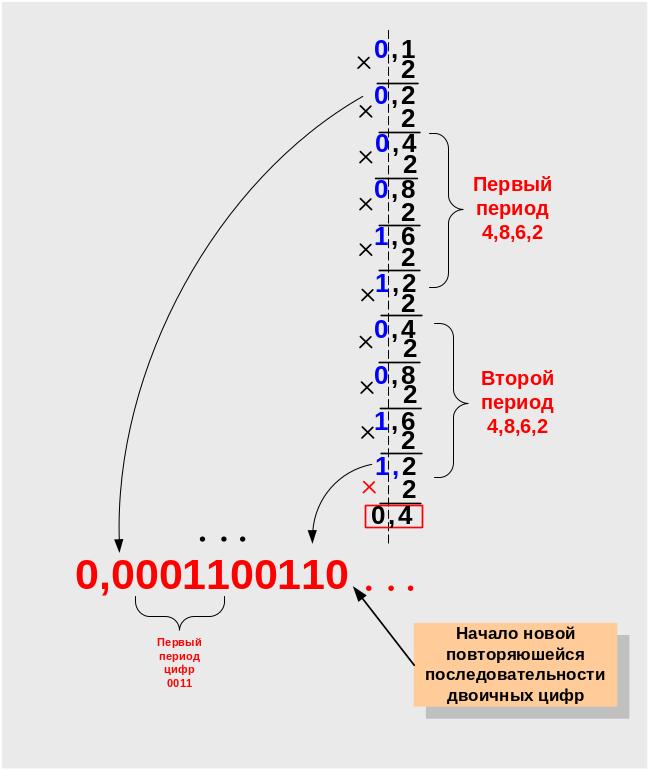
Как и при анализе методов конвертирования целых чисел необходимо выделить несколько основных свойств алгоритма “последовательное умножение”.

Первое. Алгоритм теоретически обеспечивает преобразование системы с любым основанием в заданную систему с любым основанием.

Второе. Преобразования необходимо выполнять по правилам исходной системы счисления, что не всегда удобно и привычно.

Третье. Область преимущественного использования метода для “ручных “ преобразований – преобразование из десятичного представления числа в двоичное.

Четвертое. Алгоритм хорошо формализован и эффективен для реализации на ЭВМ и МПТ.

Пятое. Конечных преобразований следует ожидать не всегда. Точность преобразований может быть ограничена длиной разрядной сетки для представления дробной части. Обычно перевод дробей из системы в систему производят приближенно.

Метод “ цифра за цифрой“ для смешанного числа

При преобразовании смешанного числа его целая и дробная часть преобразуются соответственно методами “деления лесенкой“ и “последовательного умножения“. Далее из полученных целого и дробного чисел в новой системе счисления составляется (конкетенация) преобразованное смешанное число. Целая и дробная часть числа разделяются запятой.

2.4 Специфические преобразования в классе систем с основанием “ целая степень двойки“

Т акие преобразования на практике выполняются для систем, основания которых связаны соотношением

где R – целое число

Очевидно, что практический интерес представляют взаимные преобразования в двоичной, восьмеричной и шестнадцатеричной системах счислениях. Эти задачи рассматриваются в следующих разделах

Двоично-восьмеричные и восьмерично-двоичные преобразования