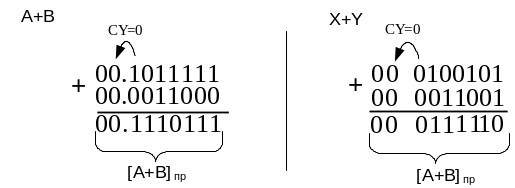3.2.1. Сложение дробных и целых положительных чисел без переполнения. (Случай 1)
3.2.1.1 Дробные числа. Пусть складываются два положительных слагаемых представленных в форме дробных чисел. Пусть также (A+B)<1. Очевидно, что сумма в этом случае – положительное число, представимое в заданной разрядной сетке т.е. переполнение в этом случае возникать не должно. Сумма должна быть сформирована прямом коде.
А
налитически
эти допущения описываются зависимостью
Соотношения (11) интерпретируется следующим образом. Вследствие ограничения (А+В)<1 отсутствует перенос CY в младший знаковый разряд из старшего разряда модуля числа. Перенос мог бы повлиять на значение знаков суммы. Содержимое знаковых разрядов определяется суммой SSA+SSB+ CY =00+00+0=00. Таким образом, сумма – положительное число, представленное в прямом коде, а переполнение отсутствует.
3.2.1.2 Целые числа. Пусть складываются два положительных слагаемых представленных в форме целых чисел. Пусть также (A+B)<2n-1. Сложение выполняется в прямых кодах. Очевидно, что сумма в этом случае должна быть положительным числом, переполнения в этом случае (см. условие 4) возникать не должно, а сумма должна быть сформирована прямом коде.
Аналитически этот случай описывается как
Как
и для дробных чисел, вследствие ограничения
(А+В)<2n-1,
отсутствует перенос CY
в знаковый разряд из старшего разряда
модуля числа. Поэтому, содержимое
знакового разряда определяется суммой
SSA+SSB+
CY
=00+00+0=00. Таким образом, сумма – положительное
число, представимое в разрядной сетке
и сформированное в прямом коде.
Пример 1. Сложение дробных и целых положительных чисел БЕЗ переполнениЯ (случай 1мдк) |
|||
Выполнить сложение в модифицированном дополнительном коде пар дробных и целых отрицательных операндов соответственно А,В и X,Y. |
|||
|
Дробные слагаемые равны |
Целые слагаемые равны |
|
А= 0.74218750=00.10111112; В=0,187510 =00.00110002 |
X= 3710=00 01001012; Y =2510=00 00110012 |
||
|
|
||
Предварительные выводы. Предварительное сложение приводит к результатам (А+В) → 0.92187510 = 00.1110112, (X+Y) → 6210 = 00 0111102. Должны быть получены положительные суммы, представленные в прямом коде. |
|||
Кроме того, так как суммы не превосходят максимальных чисел представляемых в заданной разрядной сетке, переполнение не ожидается. |
|||
Решение. Так как операнды – положительные числа, сложение выполняется в прямых кодах |
|||
Сложение в двоичных модифицированных кодах имеет вид: |
|||
|
|
|
|
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
Результаты подтверждают предварительные выводы.
|
|||
