25.161. (С) Продольная балансировка должна обеспечиваться в следующих условиях:

(1) при наборе высоты на режиме максимальной продолжительной тяги со скоростью не выше , с убранным шасси и закрылками в убранном (i) и во взлетной (ii) положениях. - скорость сваливания или минимальная скорость установившегося полета, полученная в конкретной конфигурации.

(2) при снижении с убранным газом на скорости не выше с выпущенным шасси и закрылками в убранном (i) и в выпущенном (ii) положениях, при наиболее неблагоприятной центровке, утвержденной для посадки независимо от веса ВС.

(3) во время горизонтального полета при любой скорости в диапазоне от до с убранными шасси и закрылками в диапазоне от до при выпущенном шасси. - максимальная эксплуатационная и максимальная скорость полета с выпущенным шасси.

25.173. Продольная статическая устойчивость.

(а) Для достижения и выдерживания скоростей, ниже заданной балансировочной скорости, требуются тянущие усилия ( ), а для достижения и выдерживания скоростей выше заданной балансировочной – толкающие усилия ( ).

(в) скорость полета должна восстанавливаться в пределах 10% исходной балансировочной в условиях набора высоты, захода на посадку и посадки и в пределах 73,5% исходной балансировочной скорости в условиях крейсерского полета.

(с) среднее значение должно быть не менее 0,5кгс/10 .

(А) Допускается нулевой градиент в диапазоне скоростей сигн. до .

Лекция 5. 3. Боковое движение. Боковое движение исследуется обычно в зависимости от параметров опорного продольного движения: углов атаки и тангажа, угловой скорости , скорости и высоты полета. Часто рассматривается сначала какой-либо опорный невозмущенный полет с заданным креном, углом скольжения или прямолинейный полет без крена и скольжения, а затем изучается характер изменения параметров бокового движения и т.п. в зависимости от разных факторов. Рассмотрим применяемые математические модели для аэродинамических сил и моментов в боковом движении.

3.1. Аэродинамические моменты крены и рыскания

При ассиметричном обтекании ВС воздушным потоком относительно плоскости XOY из-за скольжения возникает аэродинамическая поперечная сила, складывается из сил, действующих на фюзеляж , вертикальное оперение и гондолы двигателей

(3.1)

где:

соответствующие коэффициенты сил, площади и коэффициенты торможения потока около указанных элементов ВС. Коэффициент аэродинамической поперечной силы ВС при нейтральном положении руля направления ( )

, (3.2)

принимается и при (скольжение на правое полукрыло) , т.е. поперечная сила направлена в сторону левого полукрыла. Так как мы будем рассматривать углы скольжения в пределах ±20°, то часто принимается . При этом между поперечной силой и боковой существует связь:

С учетом малости получаем

,

или, когда значения Х невелики, то

.

Так же как и для продольного движения можно суммировать все моменты, возникающие от отдельных частей ВС, предполагая неизменной его конфигурацию. В качестве опорного движения примем прямолинейное движение с неизменной скоростью, а боковое – в малой окрестности его с отклоненными рулем направления и элеронами, со скольжением и по линейной траектории ( ).

В этом случае коэффициенты моментов крена и рыскания записываются в следующем виде

(3.3)

, (3.4)

где

В основном работа двигателей приводит к поперечной силе и моментов от нее за счет косой обдувки воздухозаборников при скольжении. определяется так же как (см. разд. 2.2). Производные моментов можно оценить так же как и в продольном движении по приближенным формулам. Чаще всего эти значения определяются и даются в зависимости от скорости полета (или М), угла атаки.

Рассмотрим здесь принятые обозначения, физическую сущность моментов, их определение. Величина принимается при в прямолинейном горизонтальном полете и зависит от скорости и балансировочного угла атаки.

Момент называют момент поперечной статической устойчивости, а - характеризует степень поперечной статической устойчивости. Все производные коэффициентов моментов являются функциями и V(M) и в частности - (при отрицательной ) будет играть роль «восстанавливающего» момента. Так, например при крене на правое полукрыло будет возникать скольжение в сторону опускающегося правого полукрыла, т.к. 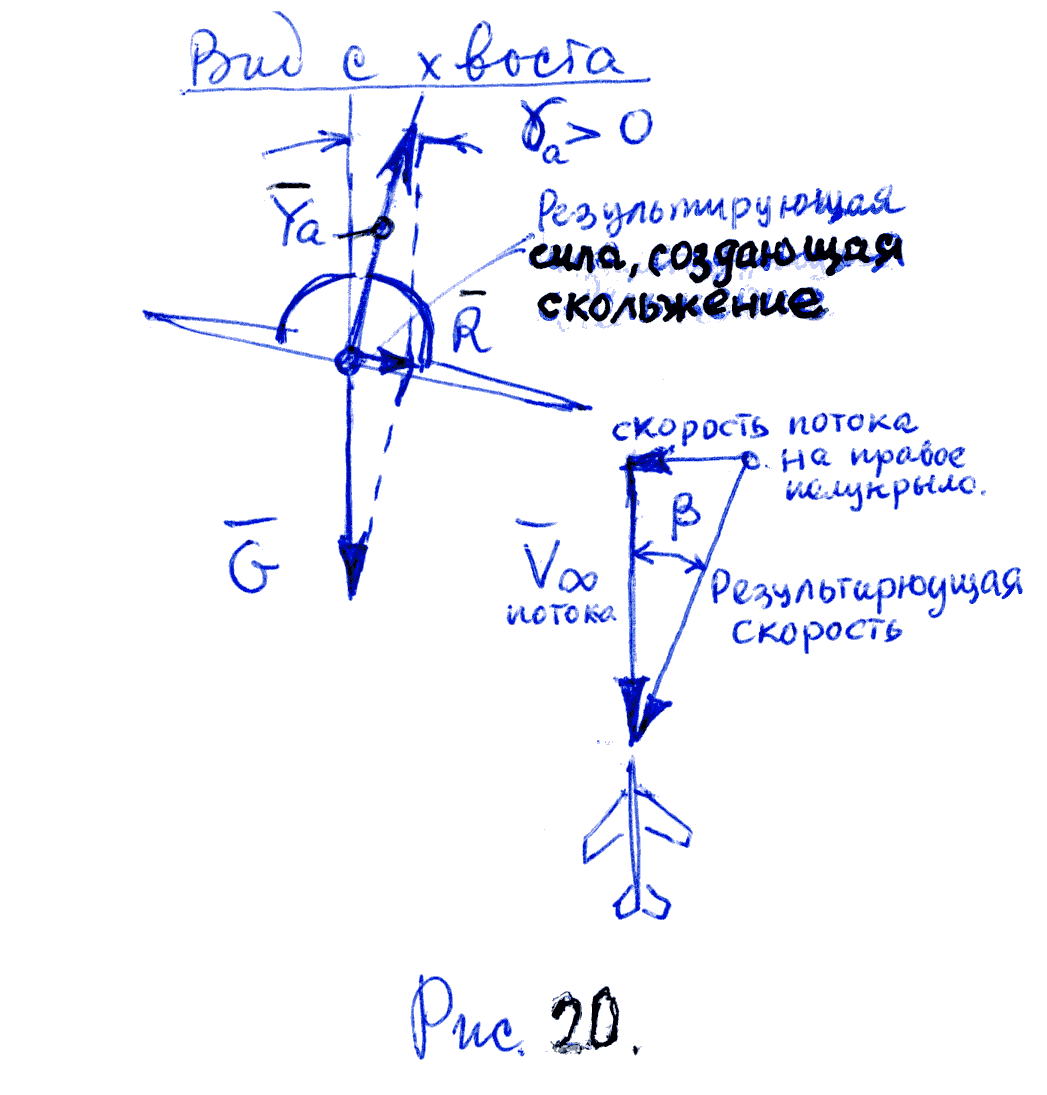результирующая сила играет роль центростремительной (см.рис. 20) неуравновешенной силы, искривляющей траекторию в сторону опущенного полукрыла и после суммирования скорости невозмущенного потока и скорости потока, набегающего на правое полукрыло, видно, что угол скольжения будет положительным.

При момент будет стремиться уменьшить величину первоначального крена , т.е. является «восстанавливающим». Моменты называются управляющими в «канале крена» и при положительных обычно являются отрицательными, т.е. <0 и <0. Моменты называют управляющими в «канале рыскания». При отклонении элеронов, например, на правом полукрыле вниз а на левом вверх происходит перераспределение давление воздушного потока ближе к концам крыльев и в результате на правом увеличится нормальная сила (также и подъемная), а на левом - уменьшится (см. рис. 21).

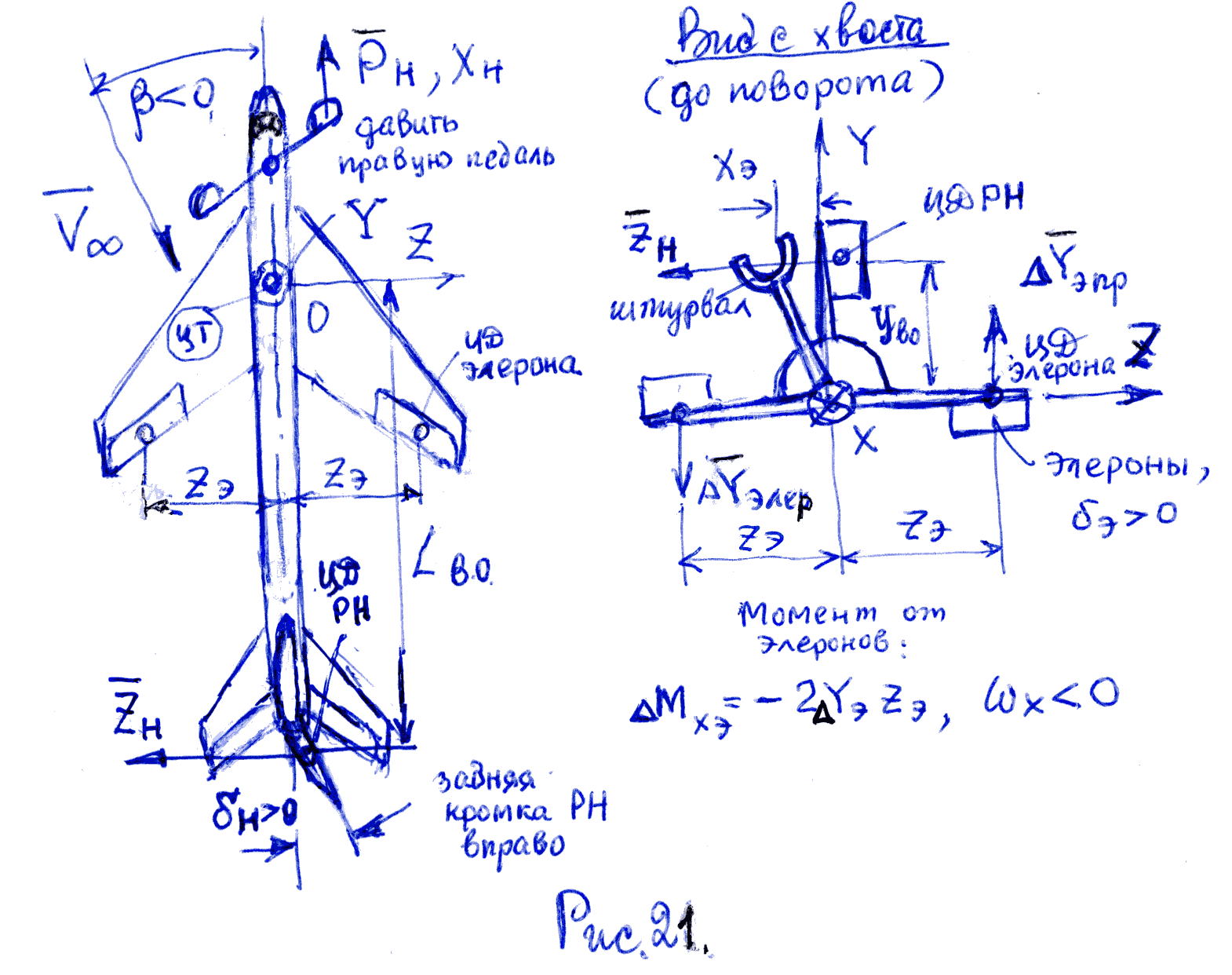
Прирост и уменьшение пропорциональны коэффициенту эффективности элеронов - и величине их отклонения . При отклонении руля направления вправо (правая педаль - вперед). На вертикальном оперении (ВО) также происходит перераспределение давлений воздушного потока и возникает дополнительная поперечная сила , которая создает на плече момент относительно ОХ и одновременно та же сила создает момент относительно OY на плече (который обычно в 5÷10раз больше )

Частная производная - называется коэффициентом эффективности руля направления. Обычно момент относительно OY в 5÷10 раз больше чем момент относительно ОХ. При отклонении РН (т.к. >> ) повернуть ВС относительно OY легче чем относительно OX (инерционные свойства ВС: сопротивление к повороту крыльев и ГО больше чем ВО) При совместном управлении элеронами и рулем направления ВС, слегка качнувшись влево, начинает разворачиваться левым полукрылом вперед, т.е. создается . на левом полукрыле возникает большая подъемная сила, чем на правом и ВС развивает положительную и положительный крен, который по отношению к моменту от элеронов будет «тормозящим» вращение.

Момент рыскания: существенно зависит от угла атаки (см. рис. 22.)

и при на малых углах , чаще всего и , т.е. развивается и положительное скольжение , которое в итоге приведет к созданию «подкручивающего момента». Аналогично можно показать, что при - моменты развиваются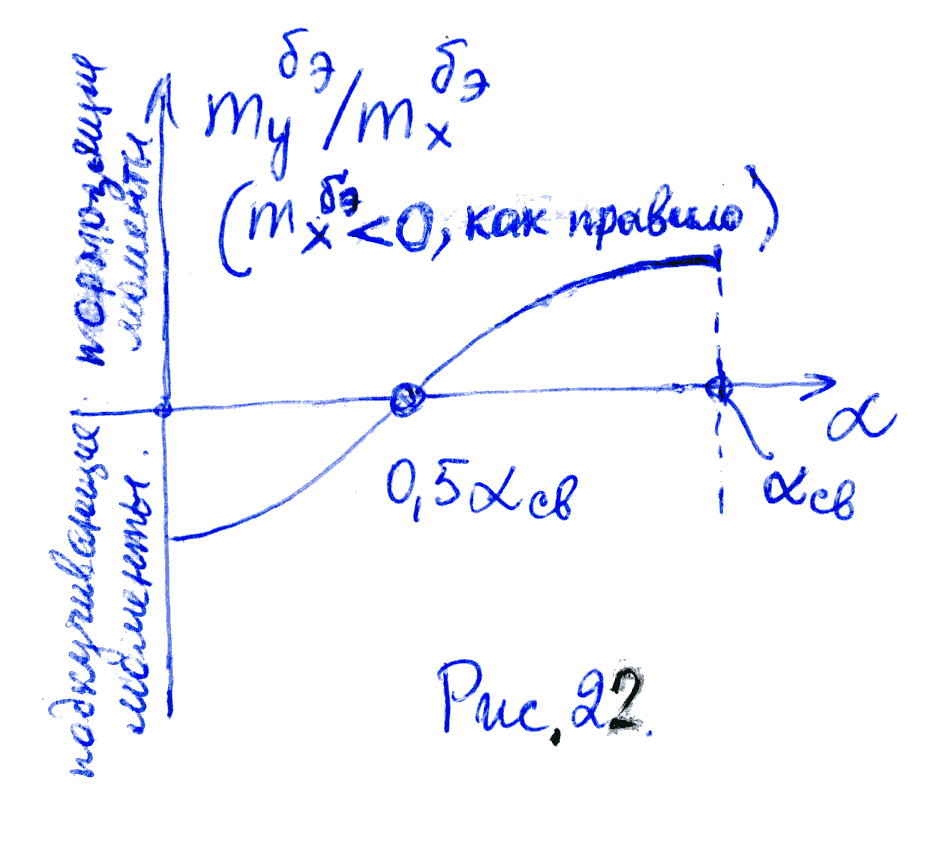

«тормозящие» (по отношению к исходным от отклонения элеронов). В зависимости от соотношения исходных моментов и «тормозящих» возможны случаи «обращения» управления.

Моменты являются демпфирующими, в линейном диапазоне изменения .Рассмотрим физическую природу этих моментов с помощью рис.23.

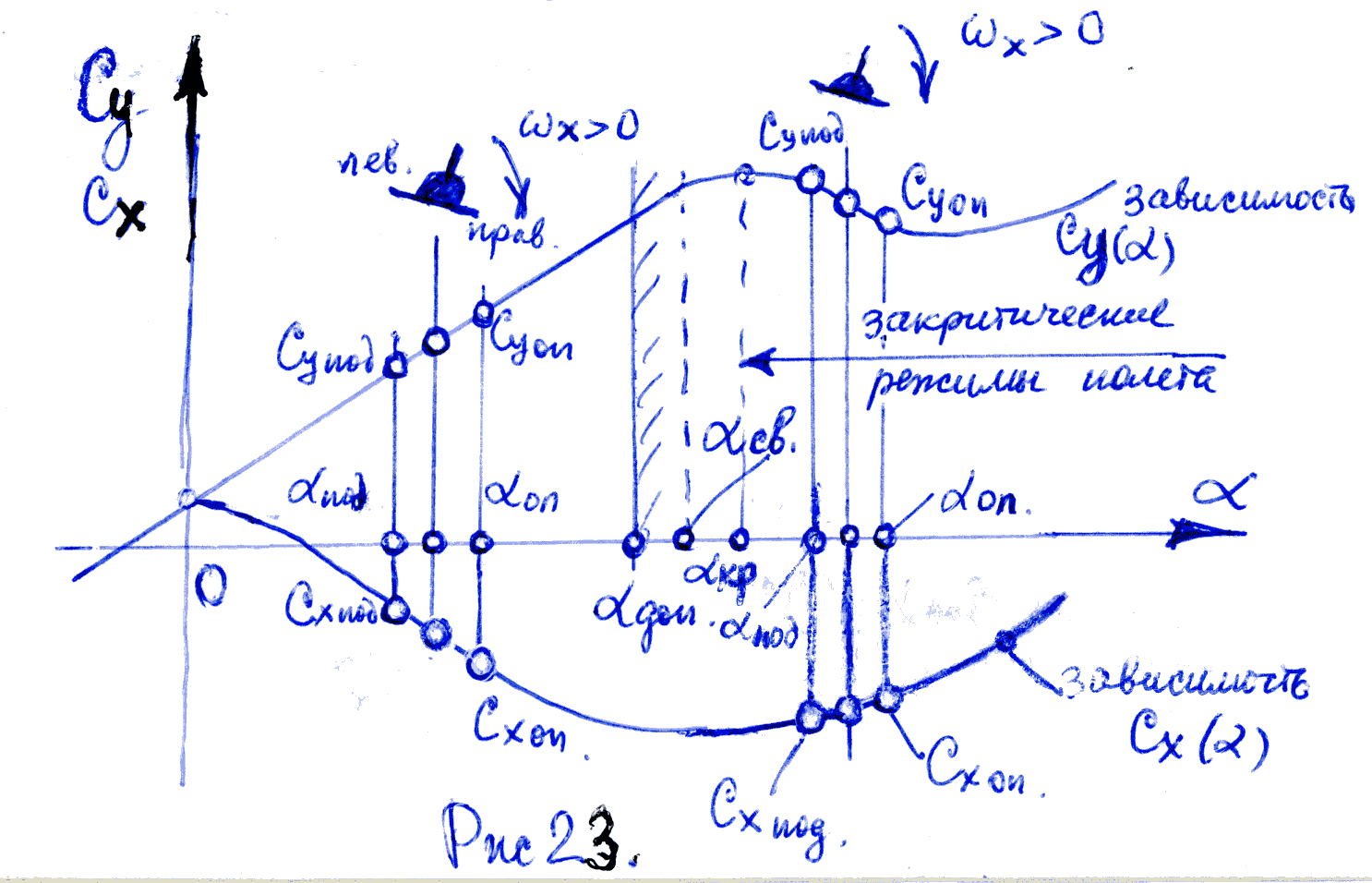
Пусть и на опускающееся правое полукрыло набегает дополнительный воздушный поток, зависящий от величины и расстояния z от OX. На опускающемся полукрыле всегда угол атаки и при , что в результате приводит к дополнительному моменту (обусловленному ), направленному в противоположную сторону вращения, тормозящему вращение, поэтому называется демпфирующим. При некоторых обычно их закритических углах атаки (режимах полета) может оказаться, что и появляется момент , подкручивающий вращение (направлен в ту же сторону). Этот момент называют авторотирующим. При одном и том же исходном угле атаки, является функцией Z и , т.е. , если принять по размаху полукрыла, то . Чем больше тем больше и возможно изменение авторотирующих моментов на демпфирующие. Все зависит от соотношения и

При варьировании изменяются соотношения и .Нормальная сила (направленная по ОХ, т.к <0, на рис.23) будет больше по модулю чем . (рис.24а)).

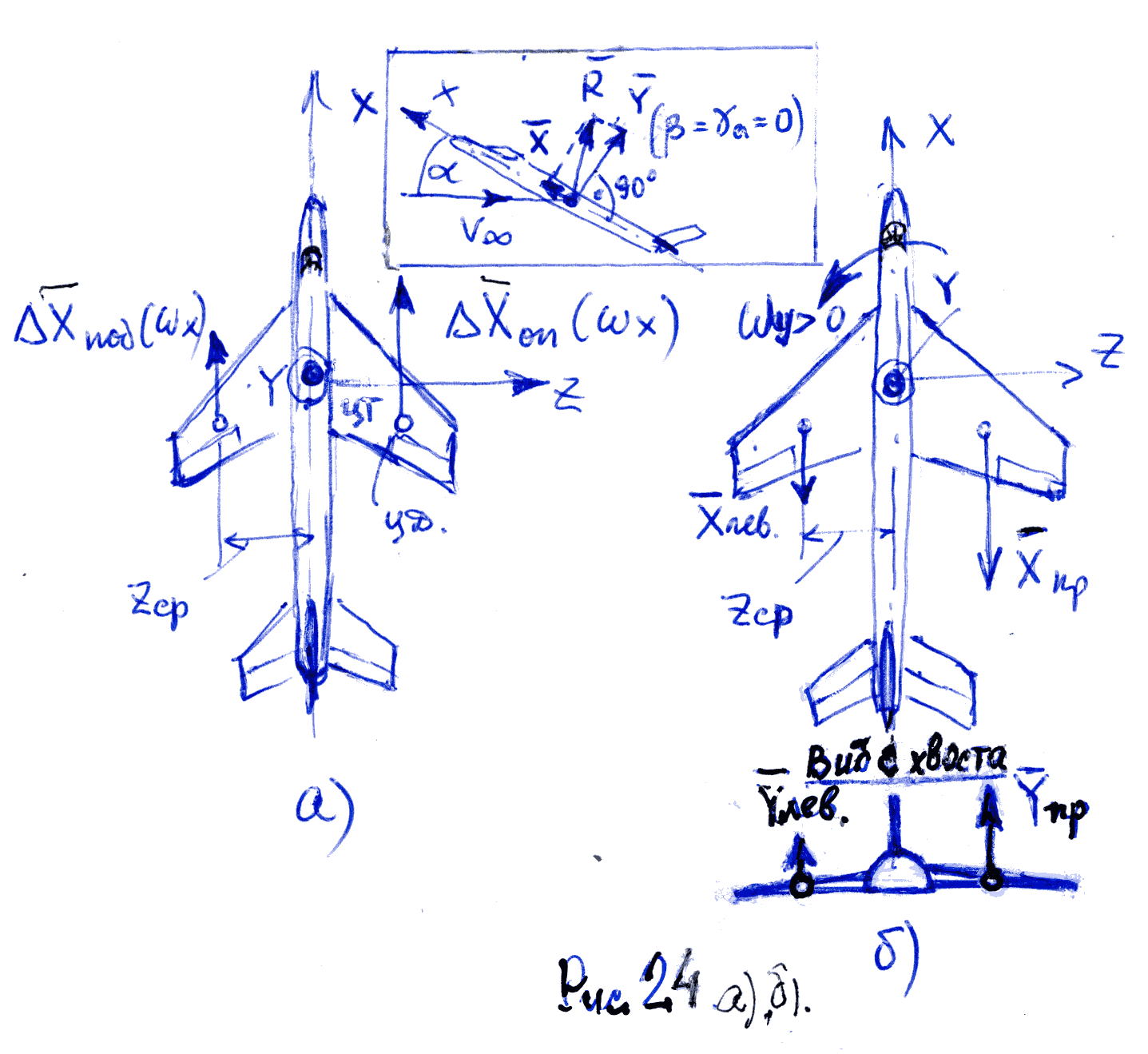
Разность этих сил создает момент относительно OY: , который называется спиральным или перекрестным моментом рыскания.

При вращении ВС относительно OY с угловой скоростью , правое полукрыло имеет большую скорость, а левое – меньшую скорость по отношению к скорости полета и и, например, для малых изображены на рис.24б). Разность этих сил создает момент ,препятствующий (тормозящий) вращение относительно OY и поэтому называется демпфирующим. Пара разностей сил по отношению к создают спиральный момент крена .