4.1.1. Решение линейных дифференциальных уравнений с постоянными коэффициентами классическим методОм. Теоремы а.М. Ляпунова об устойчивости

При исследовании собственного возмущения движения ВС выясняется устойчивость опорного движения. Анализ вынужденного движения позволяет определить реакцию ВС на управляющие воздействия и сделать оценку его управляемости. Рассмотрим решение однородной системы дифференциальных уравнений (4.4) (с целью дальнего исследования устойчивости) при ∆ .

(4.7)

Пусть по методу замороженных коэффициентов и система (4.7) приводится к виду

(Н.У.) (4.8)

Решение будем искать в виде ,где С– некоторой постоянный вектор – столбец, координаты которого зависят от выбора Н.У: ; - постоянное число. Подставим решение в исходное уравнение ,

откуда

(4.9)

Так как все элементы С не могут быть равны нулю, то для того чтобы существовало нетривиальное решение системы (4.9) относительно вектора С, необходимо и достаточно, чтобы

(4.10)

Это соотношение представляет алгебраическое уравнение n-ой степени относительно и называется характеристическим уравнением (многочленом). Его корни являются собственными числами матрицы А. Для каждого можно получить решение системы (4.9). Итак, частным решением системы (4.8) будет

(4.11)

а общее, как линейная комбинация частных решений

(4.12)

Эта линейная комбинация является общим решением системы только, если все действительны и различны. Подставляя в (4.12) Н.У., получаем при

(4.13)

Это уравнение относительно неизвестных является неоднородным и решение можно найти по формуле Крамера.

Из построенного общего решения (4.12) видно, что когда все действительны, то отклонения от невозмущенной (опорной) траектории изменяются по апериодическому (экспоненциальному) закону и будет возрастать или убывать в зависимости от знаков корней . Если все корни будут отрицательными, то при компоненты вектора стремятся к нулю и, следовательно, невозмущенное движение будет асимптотически устойчивым. Если хотя бы один из корней будет положительным, то из (4.12) видно, что компоненты будут возрастать с течением времени при сколь угодно малых начальных отклонениях и таким образом невозмущенное (опорное) движение будет неустойчивым.

Рассмотрим случай, когда среди корней характеристического уравнения имеются комплексные сопряженные. Пусть два корня: . Этим корням соответствует частное решение

,

где и определяются из системы (4.9) и являются комплексными сопряженными векторами = -i ; = +i ;

Компонент, соответствующий «S»-строке может быть представлен в виде

(здесь для простоты дальнейших преобразований принято ). Пользуясь формулой Эйлера ; , получим

, где , - новые производные постоянные. Откуда видно, что частое движение, соответствующее паре комплексных сопряжённых корней, будет колебательным с амплитудой , круговой частотой и фазой . Амплитуда будет неограниченно возрастать, если вещественная часть комплексного корня – положительная и затухать если . Поскольку общее решение будет содержать колебательную составляющую, то для устойчивости невозмущенного движения вещественные части корней должны быть отрицательными. Это, является основным содержанием теоремы А.М. Ляпунова об устойчивости по первому приближению.

Пусть исходная динамическая система описывается векторным уравнением

, (4.14)

где мерный вектор, мерный вектор, мерная непрерывная вещественная вектор-функция, заданная в ограниченной области переменных «у» и«n» и удовлетворяющая условиям Липшица.

Пусть для - начального условия в моменты времени и заданного управления получено единственное решение (4.14), которое называется невозмущенным (опорным, программным) движением.

Решение той же системы (4.14) с заданным управлением , но с другим начальным условием называется возмущенным и исследование устойчивости движения сводится к исследованию свойств решений возмущенного движения .Для анализа возмущенного движения сделаем замену переменных:

и поскольку невозмущенное движение удовлетворяет исходному уравнению(4.14)

(Н.У.)

то для возмущенного движения с учетом замены переменных, получаем

Очевидно, что исследование на устойчивость исходной системы может быть заменено исследованием на устойчивость преобразованной системы или, что одно и то же, расположенной в начале координат точки покоя . При исследовании точки покоя нелинейной системы представим ее в виде:

, (4.15)

где R(t, Δy) – имеет порядок выше первого относительно . Вместо точки покоя нелинейной преобразованной системы (4.15) будем исследовать устойчивость точки покоя Δy 0 линейной системы:

=A(t) Δy, (4.16)

называемой системой уравнений первого приближения для нелинейной (4.15).

Исследование на устойчивость линеаризованной системы остается проблематичным в случае переменной матрицы A(t) и значительно упрощается, если элементы матрицы А постоянны (A=const), т.е. исходная система и, следовательно, считать, что преобразованная стационарна в первом приближении. А.М. Ляпунов доказал основные теоремы.

Теорема об устойчивости

Если система (4.15) стационарна в первом приближении, все члены R_i в достаточномалойокрестности начала координат при t≥T≥t₀ удовлетворяют неравенствам ,

где N и α - постоянные, причем α>0 (т.е. если R_i не зависит от t, то их порядок выше первого относительно ) и все корни характеристического уравнения

|A - λ E|=0

имеют отрицательные действительные части, то тривиальное решение y 0 системы уравнений (4.15) и решение системы уравнений (4.16) асимметрически устойчиво, следовательно, в этом случае возможно исследование на устойчивость по первому приближению.

Теорема о неустойчивости

Если в условиях первой теоремы хотя бы один корень характеристического

уравнения имеет положительную действительную часть, то точки покоя Δy 0 системы (4.15) и (4.16) неустойчивы, следовательно, и в этом случае возможно исследование на устойчивость по первому приближению.

Эти теоремы не охватывают случай, когда корни характеристического уравнения чисто мнимые (или когда вещественная часть хотя бы одного корня равна нулю). В таком критическом случае начинают влиять на устойчивость нелинейные члены R_i и исследование на устойчивость по первому приближению, вообще говоря, невозможно.

Непосредственное исследование устойчивости невозмущенного движения (или точки покоя Δy 0 преобразованной системы) является простым лишь для уравнений первого и второго порядков. Поэтому для решения вопроса об устойчивости или неустойчивости разработаны косвенные признаки, по которым можно судить о знаке вещественной части корней характеристического уравнения, минуя вычисление самих корней, которые называются критериями устойчивости.

По критериям устойчивости можно судить об устойчивости линейной стандартной системы, определять границы устойчивости и выбирать параметры устойчивой системы.

Критерии устойчивости подразделяются на алгебраические и частные. Алгебраические критерии позволяют судить об устойчивости и неустойчивости систем по коэффициентам характеристического уравнения. Имеются различные формы критериев. Наибольшее применение получили критерии Гурвица и Рауса.

Приведем без доказательства теорему Гурвица.

Пусть характеристическое уравнение n-ой степени имеет вид

a_nλⁿ+a_n-1λ^n-1+…+a₁λ+a₀=0 (4.17)

в котором все коэффициенты a_k – вещественные числа, а a_n>0. Построим из коэффициентов a_k матрицу Гурвица (nxn):

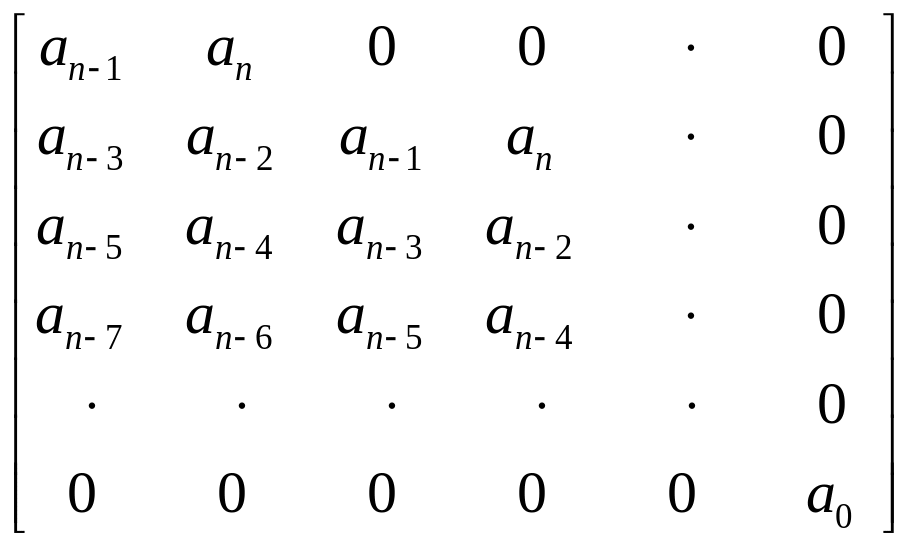
Теорема Гурвица

Для того чтобы все корни характеристического уравнения (4.17) имели отрицательные вещественные части, необходимо и достаточно, чтобы все главные диагональные миноры матрицы Гурвица были положительны:

Δ₁ = a_n-1>0; ; …; Δ_n = a₀ Δ_n-1>0. (4.18)

Пример: Дано уравнение четвертой степени

λ⁴+a₃λ³+a₂λ²+a₁λ+a₀=0 (a₄=1) (4.19)

Для «устойчивого движения» должны выполняться условия

Δ₁ = a₃>0; ; ; Δ₄ = a₀ Δ₃ > 0.

Равносильными для уравнения 4-ой степени являются условия Рауса-Гурвица:

a₀>0; a₁>0; a₂>0; a₃>0; R=Δ₃=a₁ a₂ a₃ - a₁²-a₀ a₃²>0. (4.20)

Найдем границы устойчивости

На границе устойчивости будут равны нулю действительный корень (λ=0) или вещественная часть комплексных сопряженных корней: ; ( ). Если подставить в (4.17) значение λ = 0, то получим границу апериодической устойчивости, а₀=0 или Δ_n = 0 (при всех остальных положительных минорах матрицы Гурвица). Подставляя в уравнение (4.17) вместо его значения: , получим границу колебательной устойчивости: , причем все остальные миноры матрицы Гурвица положительны. Третья граница устойчивости соответствует бесконечному корню и согласно уравнению (4.17) будет при а_n = 0 (что на практике встретить затруднительно).