2.1. Аэродинамический момент тангажа в установившемся прямолинейном полете.

Выделяя основные составляющие, момент М_z удобно представить как алгебраическую сумму аэродинамических моментов тангажа ВС без ГО момента ГО (при нейтральном положении органов управления ) и управляющих моментов ВС :

Второй из перечисленных моментов тангажа в зависимости от угла установки стабилизатора - , фактически также является управляющим и может быть объединен с последним.

Рассмотрим аэродинамический момент тангажа в установившемся (V=const) прямолинейном (θ=const) полете без крена ( =0) и скольжения (β=0).

Для ВС нормальной схемы (см. рис.6), условно в прямолинейном полете близком к горизонтальному (Н ≈ const, ) показаны аэродинамические силы (за исключением Х_а), которые создают основной момент относительно ОZ. Подъемная сила всех частей ВС за исключением ГО , зависящая от угла атаки (кроме )приложена в фокусе ВС без ГО (обозначен ).

Под фокусом по углу атаки будем понимать точку пересечения линии действия полной

аэродинамической силы зависящей только от угла атаки, с продольной осью ВС.

В частности вместо составляющей полной аэродинамической силы с некоторой погрешностью можно принять составляющую подъемной силы, зависящей от угла атаки.

Если ось OZ поместить в эту точку и вычислить продольный момент то в силу равенства нулю плеча действия сил, зависящих от , производная момента при всех осталь-

ных фиксированных параметрах: и т.д.

Так же как и аэродинамические силы по принципу суперпозиции складываются из сил,

действующих на отдельные части ВС (крыло, фюзеляж и др.) так и фокус (для краткости «по углу атаки » будем опускать) зависит от фокуса крыла, фюзеляжа и др. Поэтому можно считать, что подъемная сила всех частей ВС без ГО приложена в фокусе всех частей ВС без ГО. При этом полная подъемная сила (для статически устойчивого ВС)

Здесь отметим, что аналогично можно ввести понятия фокуса по отклонению руля высоты,

закрылков и др. отклоняемых органов управления при малых их отклонениях и фиксированных остальных параметрах (углах).

Аэродинамический момент тангажа ВС запишем в следующем виде

где

Здесь индексами обозначены составляющие момента тангажа: «кр»- от крыла; «ГО»-от горизонтального оперения; «ф»- от фюзеляжа; « »-от гондол двигателей; «подв»- от различных подвесок. Можно обозначить М_z от всех частей кроме ГО как , а момент от стабилизатора и руля высоты .

Из рис.6. видно, что для сбалансированных режимов полета момент от всех частей без ГО <0 (на пикирование) должен уравновешиваться моментом, создаваемым ГО, >0 (на кабрирование). При этом результирующая подъемная сила направляется вниз при отрицательном отклонении руля высоты < 0 (задняя кромка - вверх) и тогда суммарная подъемная сила, которая в основном уравновешивает силу тяжести (например, в горизонтальном полете) определяется в виде разности сил , что является невыгодным с точки зрения создания полной подъемной силы и этот случай кратко называют «потерей на балансировку».

При малых углах атаки, полагая приближенно и можно записать выражение для момента тангажа (см. рис. 6)

, (2.1)

где: - момент тангажа ВС без ГО при α = 0; ; - угол атаки горизонтального оперения, ε – скос потока в области ГО, приближенно зависящий от α и С_yaб.г.о. линейно:

.

Подставив это соотношение в выражение для α_г.о., получаем (прибавляя и вычитая α_об.г.о.)

= (2.2)

Преобразуем (2.1), принимая во внимание (2.2), выражения для и поделив на qSb_A

, (2.3)

где: коэффициент торможения потока у ГО, ; - относительная площадь ГО; - относительное плечо ГО; - относительный статический момент площади ГО; полагая малой величину , коэффициент представим в виде

(2.4)

Преобразуем выражение (2.3), учитывая (2.2), (2.4)

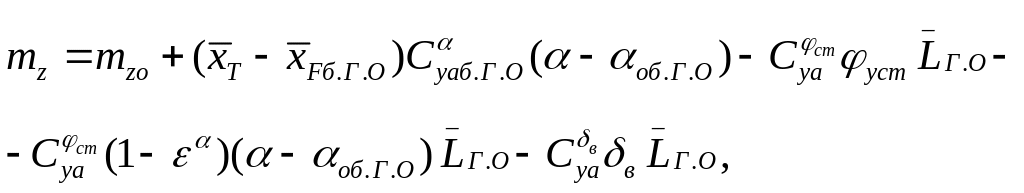(2.5)

где обозначены: ;

- коэффициент относительной эффективности руля высоты; при М<1, S_в – площадь руля высоты.

С целью дальнейшего упрощения выражения (2.5), установим соотношение между . При этом рассмотрим часть подъемной силы, зависящую только от угла атаки с учетом (2.2).

Откуда при , получаем

(2.6)

Преобразуем теперь составляющие (2.5), являющиеся множителями при α с учетом предыдущего соотношения

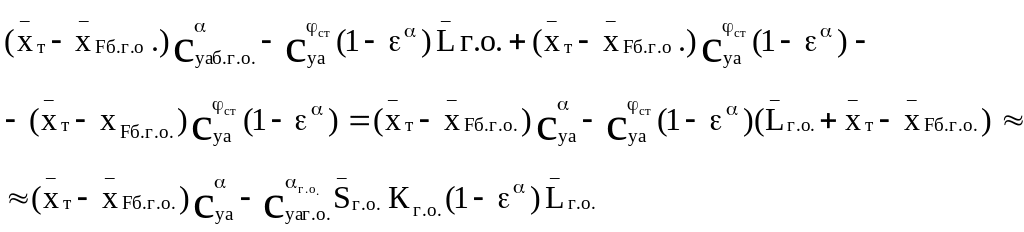(2.7)

(с точностью до в предыдущем соотношении (2.7)).

Введем обозначения

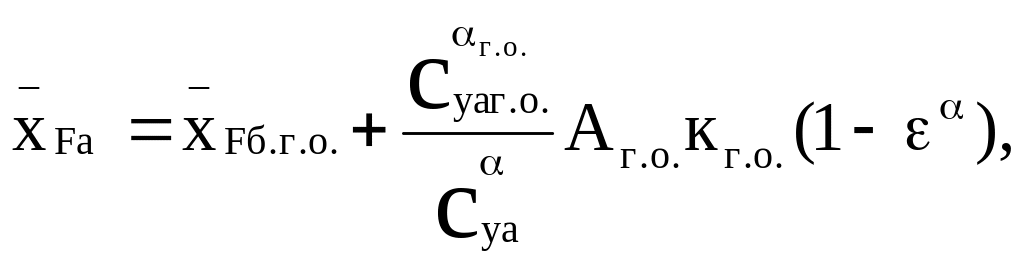(2.8)

тогда (2.7) преобразуется к виду

(2.9)

и коэффициент момента тангажа (2.5), с учетом (2.9), запишем в новой форме

(2.10)

где обозначены:

(2.11)

(2.12)

Учитывая, что можно (2.10) записать в другом виде

(2.13)

где

(2.14)

При этом имеется в виду, что зависит только от α при нулевых , а общая зависимость (в линейном диапазоне изменения ) имеет вид

(2.15)

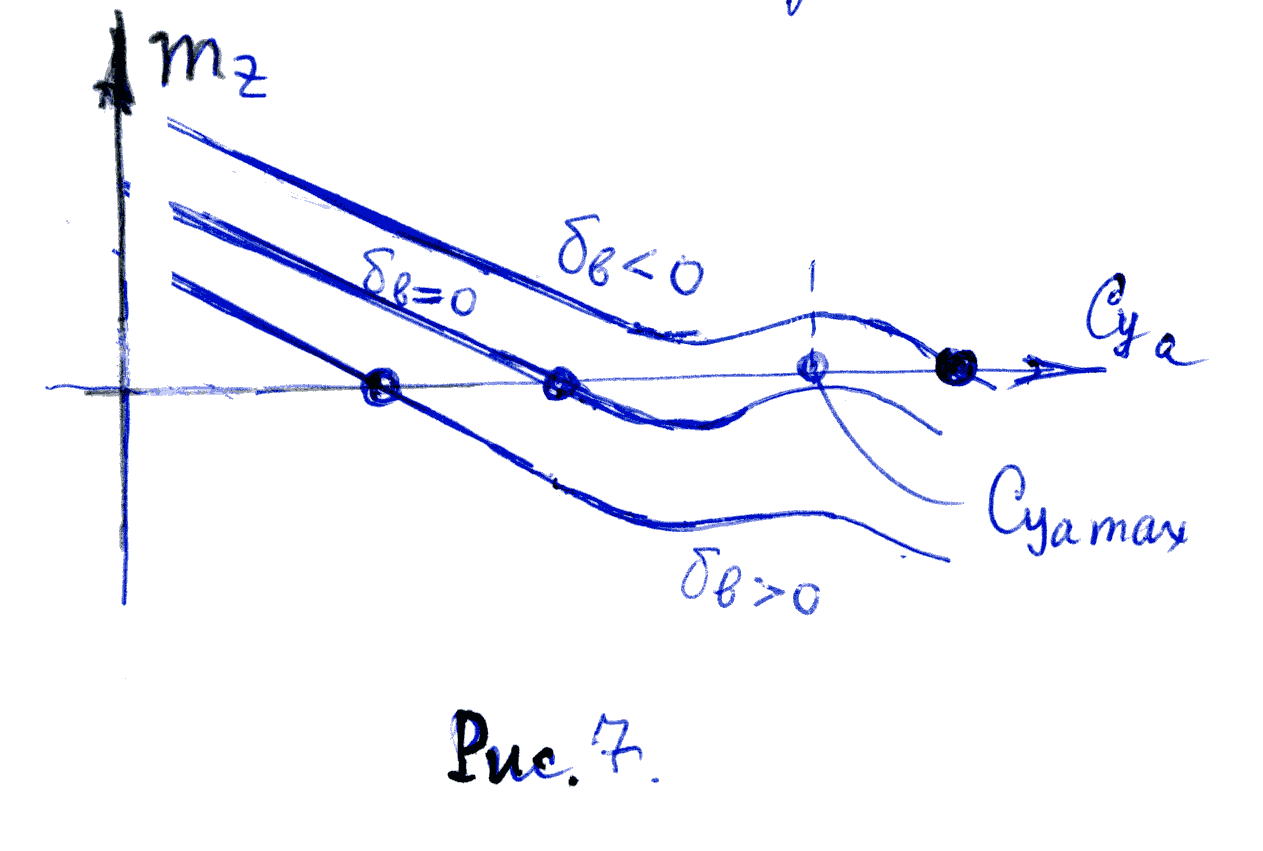
при переменном . Если вместо руля высоты используется управляемый стабилизатор, то надо принять в (2.13) Примерная зависимость (2.13) для ВС нормальной схемы при М=const; имеет вид