6.3Передаточные функции в боковом возмущенном движении
Изолированное движение рыскания. Из системы (6.12) после преобразования Лапласа получаем
;
(6.20)
где:
;
;
;
;
;
hδ – декремент затухания углового движения в боковой плоскости;
ωδ – частота недемпфированных колебаний в боковом движении.
.
(6.21)
Изолированное движение крена
В уравнениях (6.12) пренебрегаем составляющими
и
и после преобразования Лапласа получаем
;
(6.22)
где:
;
;
.
(6.23)
Из первого уравнения системы (6.1),
предполагая
(угол
«установился»),
при
малых и после преобразования Лапласа
.
(6.24)
Здесь
,
(см.(5.37));
Траекторное движение центра масс
ВС. Будем предполагать, что ВС
сбалансировано по моментам
откуда
Примем, что:
где
(6.25)
Рассмотрим уравнение для
системы
(6.1)
Здесь выражение в скобках соответствует
приближенно углу пути
,
т.е. можно записать
Продифференцируем это уравнение по времени
где приближенно
и соответствующая система уравнений
возмущенного траекторного движения
может быть представлена в следующем
виде
(6.26)
После преобразования Лапласа, определяются передаточные функции:
;
(6.27)
Рассмотрим основные передаточные функции в боковом возмущенном движении во взаимосвязи между собой
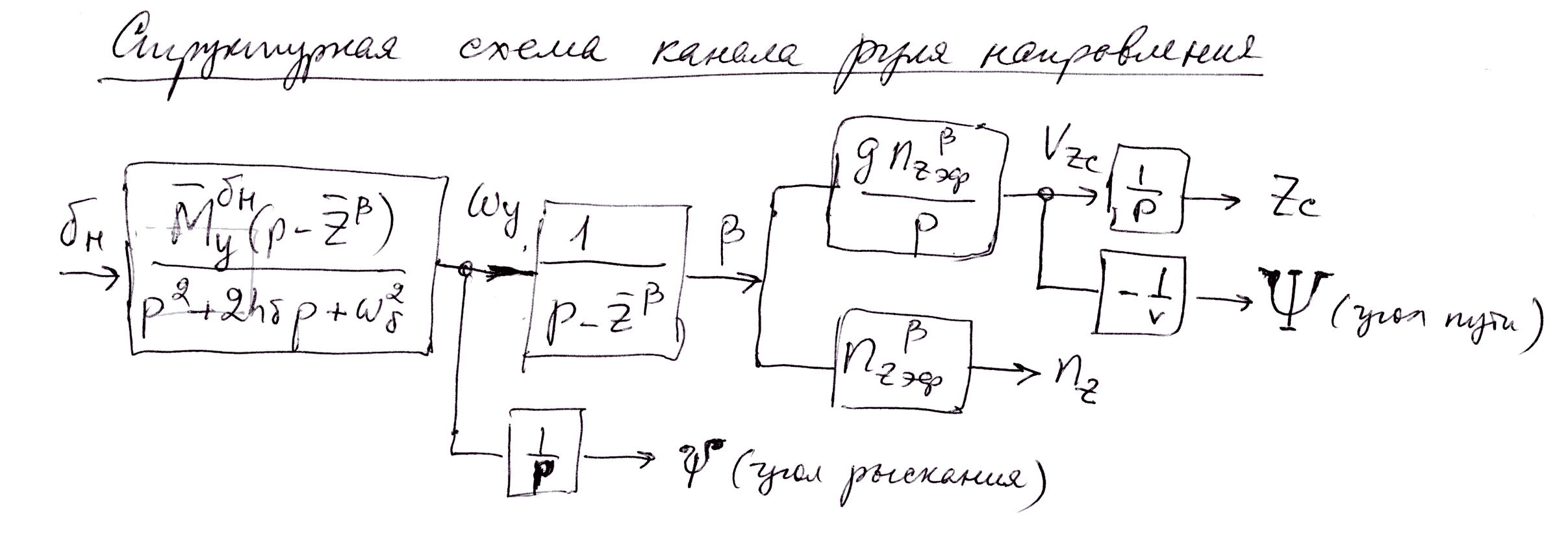
6.4. Анализ переходных процессов в боковом возмущенном движении.
6.4.1. Реакция ВС на отклонение элеронов
Для определения характеристик переходного процесса необходимо рассмотреть переда-
точную функцию
более общего вида, чем ранее. С этой
целью в уравнении
(см. систему (4.6)) для
учитывается
составляющая
,
и в итоге получаем
(6.28)
где
.
Характер переходных процессов по
определяется параметром
(6.29)
и при
(
)
переходный процесс
имеет апериодический характер.
В этом случае передаточная функция
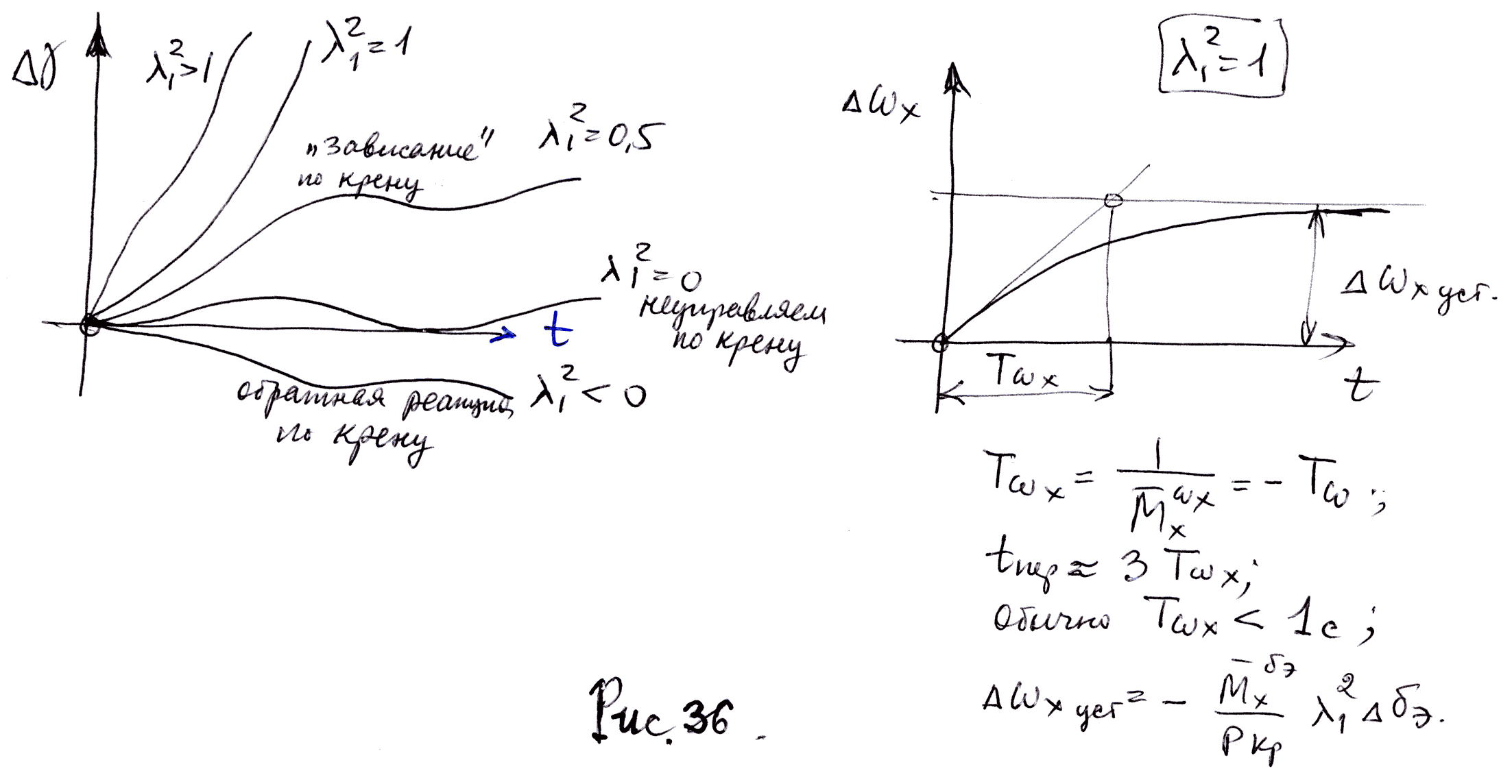
принимает вид (6.23) На рис. 36 представлены
переходные процессы по углу крена при
различных значениях
и
