5. Динамика продольного возмущенного движения вс

В разделе 4 получены формулы (4,5), описывающие продольное возмущенное движение. Принимается β=γ_a=0, m(t)=const, изменение аэродинамических сил по высоте мало,

, , ;

пренебрегается изменением по высоте ρ(H), p(H), a(H), полагая момент тангажа сбалансированным в опорном движении . Для упрощений уравнений возмущенного движения целесообразно перейти от производных сил к производным перегрузок, учитывая что

nya= (P sin(α+φ_p)+Ya); nxa= (P cos(α+φ_p)-Xa);

при (γa=0, β=0): nya=nyk; nxa=nxk; M= ; .

Проделаем преобразования на примере первого уравнения и уравнения для описания опорного движения . Уравнение в отклонениях от опорного (возмущенного ) запишем в виде (принимая во внимание: )

Проделав аналогичные преобразования можно уравнения (4.5) представить в матричной форме.

, (5.1)

где

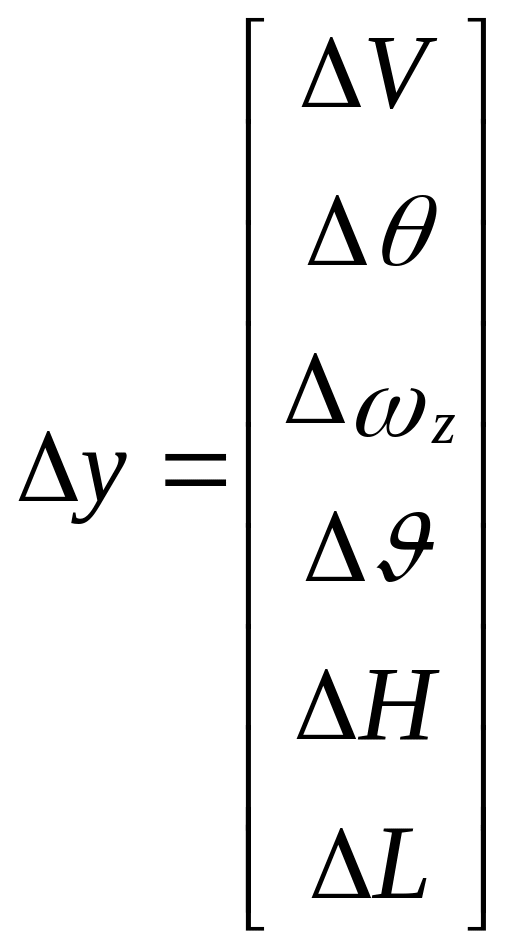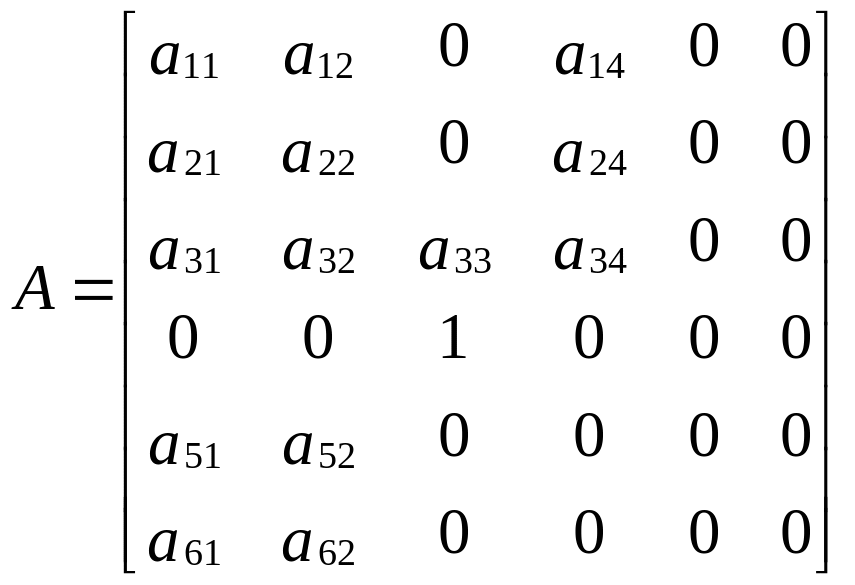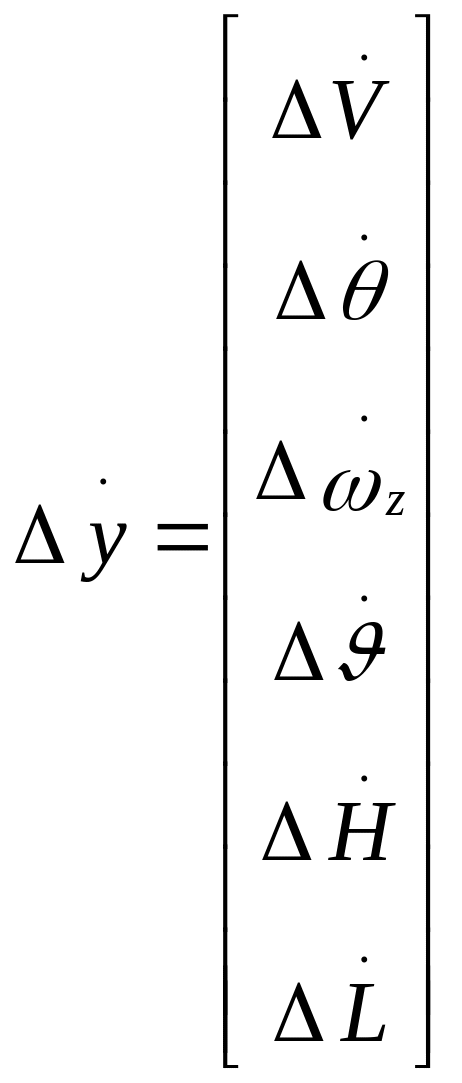; ; ; ; ; (5.2)

a₁₁ = g n_xk^V = n_xk^M M; a₂₁ = (n_yk^M M – n_yk + cos θ); a₁₂ = g(n_xk^θ – cos θ)=g(-n_xk^α – cos θ);

a₂₂ = (n_yk^θ + sin θ) = (-n_yk^α + sin θ); a₁₄ = = g n_xk^α; a₂₄ = = n_yk^α;

D_z= ; a₃₁ = (2m_z + 2m_pz1 + m_z^M M + m_pz1^MM); a₃₂ = D_z m_z^θ; a₃₃ = D_z m_z^ωz;

a₃₄ = D_z ; a₅₁ = sin θ; a₅₂ = V cos θ; a₆₁ = cos θ; a₆₂ = -V sin θ; b₁₁ = g ;

b₂₁ = ; b₃₁ = D_z ; b₂₂ = n_yk^δв; b₃₂ = D_z m_z^δв.

В системе (5.1) параметры ΔH и ΔL не входят в правые части четырех первых уравнений и нe влияют на изменение соответствующих фазовых переменных, поэтому могут рассматриваться независимо от двух последних.

5.1. Собственное продольное возмущенное движение вс. Условия устойчивости опорного движения

В опорном режиме полета управление u˚(t) = (P˚(t), δ_b˚(t)) задано и изменение Рассмотрим уравнения продольного собственного возмущенного движения (см. (5.1), без включения строк и столбцов, соответствующих ΔH и ΔL).

(5.3)

Характеристический многочлен

|A - λE| = |λE - A| = 0, (5.4)

или

.

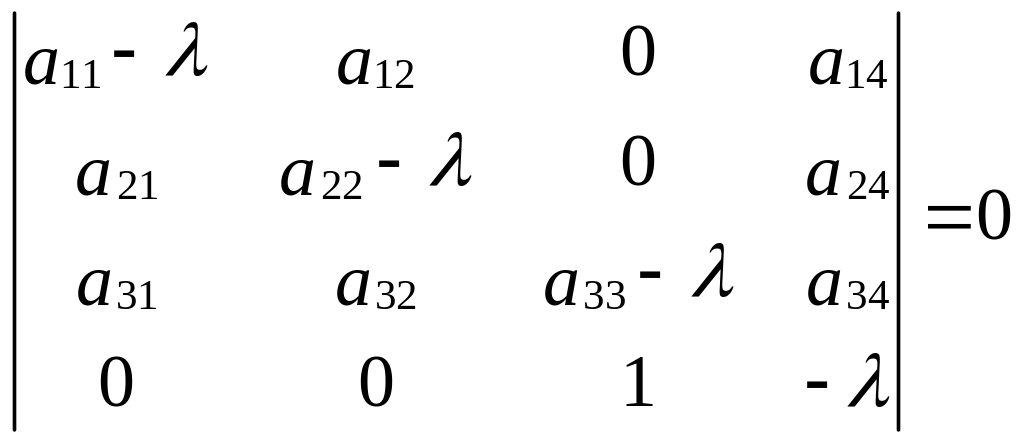Раскрывая определитель по последней строке, получаем:

λ⁴ + a₃ λ³ + a₂ λ² + a₁ λ + a₀ = 0, (5.5)

где: a₃ = -a₁₁ – a₂₂ – a₃₃; a₂ = a₁₁ a₂₂ + a₂₂ a₃₃ + a₁₁ a₃₃ – a₂₁ a₁₂ + a₃₄;

a₁ = - a₁₁ a₃₄ – a₂₂ a₃₄ + a₃₁ a₁₄ + a₃₂ a₂₄;

a₀ = a₁₁ a₂₂ a₃₄ + a₂₁ a₃₂ a₁₄ + a₃₁ a₁₂ a₂₄ – a₃₁ a₁₄ a₂₂ – a₂₁ a₁₂ a₃₄ – a₁₁ a₃₂ a₂₄.

Для асимптотической устойчивости в соответствии с условиями Рауса – Гурвица должно соблюдаться:

a₀>0; a₁>0; a₂>0; a₃>0; R = a₁ a₂ a₃ – a₁² – a₀ a₃²>0.

Возмущенное движение в целом по всему вектору Δy = (ΔV, Δθ, Δω_z, Δ , ΔH, ΔL) можно проанализировать по уравнениям для ΔH и ΔL, т.е. пусть = V Δθ; = ΔV. Интегрированием этих уравнений получаем:

ΔH(t) = V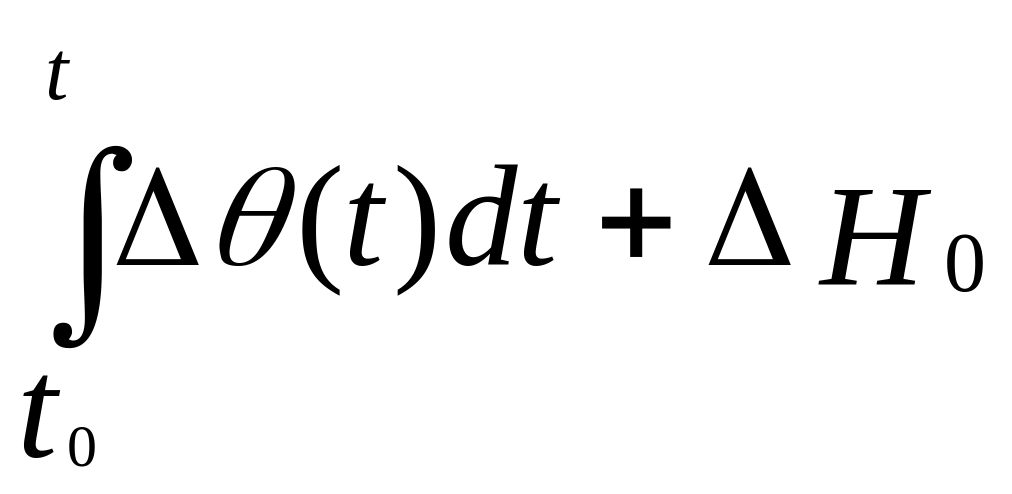 ; (ΔH₀≠0)

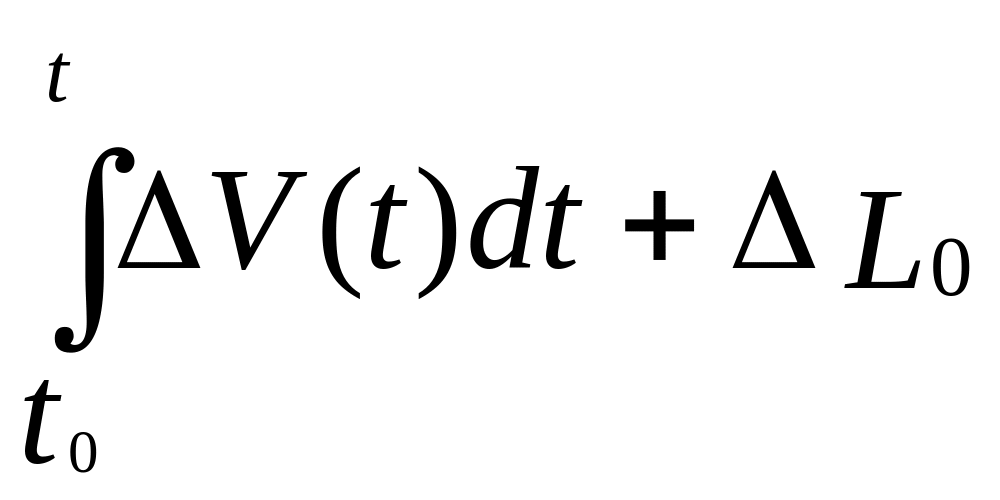ΔL(t) = ; (ΔL₀≠0)

Откуда видно, что если ВС асимптотически устойчиво по Δθ(t) и ΔV(t), т.е. при t→∞ Δθ(t)→0, ΔV(t)→0, то при этих условиях ΔH(t)→ΔH₀ и ΔL(t)→ΔL₀ и движение не будет асимтотически устойчивым, но может быть просто устойчивым по Ляпунову при малых ΔH₀ и ΔL₀.