Книги и конспекты / Горьковой Дискретная Математика

2.2. Матрицы отношений

Пусть заданы пронумерованные конечные множества

X = {x1, . . . , xm } и Y = {y1, . . . , yn}.

Тогда таблица из нулей и единиц, задающая любое отношение α, представляет собой m × n-матрицу A = kaij k :

В примере 6 матрицы A, B, отвечающие соотношениям α, β, имеют вид

Обратно, любая m × n-матрица A = kaij k из нулей и единиц определяет отношение ρ(A) по формуле (2.2.1). Поэтому всякую (прямоугольную) матрицу из нулей и единиц мы будем называть матрицей отношения.

На пересечении i-й строки и j-го столбца матрицы M (α) = A любого бинарного отношения α между множествами X и Y стоит элемент aij , значение характеристической фукции e = eS(α) : X × Y → {0, 1} графика S(α) X × Y отношения α. Иными словами,

Каждое бинарное отношение α между X и Y определено его графиком S(α) и каждое подмножество T X × Y является графиком единственного бинарного отношения ρT между X и Y , которое определяется условием xρT y тогда и только тогда, когда (x, y) T . Поэтому соответствия α → S(α) и T → ρT определяет взаимно обратные биекции множества всех бинарных отношений между X и Y и множества всех подмножеств P (X × Y ) произведения X × Y :

21

Кроме того, S(α′) = [S(α)]′ : отрицание отношения в этой биекции отвечает взятию дополнения к графику. По этой причине α′ также называется дополнением к отношению α.

Б у л е в ы о п е р а ц и и. Описанные биекции приводят к рассмотрению булевой алгебры, элементами которой являются бинарные отношения между X и Y . Введем операции и следующим образом:

для любых двух отношений между X и Y и любых двух подмножеств T, V X ×Y. В частности, для любых двух дополнительных отношений, таких как α и α′ = β в примере 6, S(α α′ ) = (пустое множество) и S(α α′) = X × Y. Мы будем называть α β пересечением бинарных отношений α, β, а α β — их объединением. Наконец, будем писать α ≤ β, если S(α) S(β). Иными словами,

2.3. Алгебра отношений

Бинарные отношения между множествами, кроме общих свойств булевых алгебр, обладают многими алгебраическими свойствами. Например, по любому отношению α между множествами X и Y можно определить обратное отношение α˘ между X и Y следующим образом:

Очевидно, что матрица k˘aij k отношения α˘ получается транспонированием матрицы kaij k отношения α, т. е. заменой строк столбцами и наоборот (отражением относительно главной диагонали в

случае m = n). Иными словами, a˘ij = aji.

Только в исключительном случае и отношение и обратоное к нему могут одновременно соответствовать функциям. Тогда, полагая α = ρf и α˘ = ρg , имеем: каждый элемент y Y (поскольку g

22

— функция) должен отвечать некоторому элементу x X, и притом единственному (поскольку f — функция). Поэтому функции f и g, отвечающие α и α˘, должны быть взаимно обратными биекциями. Их матрицы отношений (если они существуют) должны быть квадратными матрицами перестановок, у которых в любой строке и в любом столбце имеется ровно одна единица.

Понятие композиции двух функций можно обобщить на отношения. Пусть α, β — отношения между X, Y и Y, Z соответственно. Тогда композицией αβ называется отношение x(αβ)z тогда и только тогда, когда существует такой

Если α = ρf и β = ρg отвечает функциям, то αβ = ρg◦f , т. е. композиция отношений отвечает композиции функций.

которое обобщает соотношение (f g)−1 = g−1 f −1.

Б и н а р н ы е о т н о ш е н и я на S. Бинарное отношение между множеством S и им самим (т. е. X = Y = S ) называется отношением на множестве S. Важным частным случаем этого понятия является отношение равенства e на S : xey означает x = y. Ясно, что на множестве n ему отвечает единичная матрица. Это квадратная матрица n × n с единицами на главной диагонали и нулями на остальных местах:

1 если =

= k ij k где ij = , i j,

I δ , δ 0, если i =6 j.

Из (2.3.2) следует, что композиция любых двух отношений на множестве S существует. Отношение равенства e удовлетворяет условиям eα = αe = α для всех α. Наконец, справедлив ассоциативный закон

α(βγ) = (αβ)γ для любых отношений α, β, γ на S. (2.3.4) Действительно, оба утверждения x[α(βγ)]y и x[(αβ)γ]y означа-

ют, что для подходящих элементов z1, z2 S имеют место утверж-

дения xαz1, z1βz2 и z2γy.

23

Резюмируем сказанное:

Теорема 5. Бинарные отношения на множестве S относительно композиции образуют алгебраическую систему, которая ассоциативна и в качестве единицы имеет отношение равенст-

ва.

Существует много важных типов бинарных отношений на S. Если xαx для всех x S, отношение α называется рефлексивным. Если из xαy следует, что yαx, отношение α называется симметричным, а в противном случае — асимметричным. Если x = y, то из xαy, очевидно, следует, что yαx; обратно, если из xαy и yαx следует, что y = x, отношение α называется антисимметричным.

Мы видели, что отношение включения между множествами рефлексивно и антисимметрично. Поэтому таково же отношение включения между отношениями.

Бинарное оотношение α на множестве S называется транзитивным, если из xαy и yαz (x, y, z S) вместе следует, что xαz. В частности, отношение включения между множествами транзитивно.

Пусть, например, T = {1, 2, 3}, и α — отношение на T с графиком

S(α) = {(1, 1)(1, 2)(2, 1)(2, 2)(2, 3)(3, 2)(3, 3)}.

Это отношение рефлексивно и симметрично, но не транзитивно, ибо 1α2 и 2α3, но 1α′3. Заметим, что график S(α2) отношения α2 совпадает с T × T . Таким образом, α2 — отношение, выполняющееся на всем T : xα2y для всех x, y T .

Данные выше определения можно переформулировать следующим образом. Бинарное отношение α на S рефлексивно тогда и только тогда, когда оно содержит отношение равенства e (e ≤ α ) или, что то же самое, когда e α = e и e α = α. Оно симметрично в том и только том случае, когда α = α˘. Оно антисимметрично тогда и только тогда, когда α α′ ≤ e. Оно транзитивно тогда и только тогда, когда α2 ≤ α (где α2, конечно, есть αα).

Если S = n, рефлексивность отношения на S означает, очевидно, что все диагональные элементы матрицы этого отношения равны единице. Отношение α симметрично в том и только том случае, когда матрица kaij k симметрична (т. е. aij = aji для всех i, j).

Наконец, понятие декартова произведения функций обобщается на отношения следующим образом. Пусть α — бинарное отношение между множествами A и Y , а β — между множествами B и

24

Y . Определим декартово (или прямое) произведение γ = α × β как отношение между множествами A × B и Y вида

Аналогично, пусть ξ — бинарное отношение между множествами A и X, а η — бинарное отношение между множествами A и Y . Определим отношение ζ = ξ × η следующим образом:

2.4. Частичное упорядочение.

Бинарное отношение на множестве S называется частичным упорядочением этого множества (или частичным поядком на нем), если оно рефлексивно, антисимметрично и транзитивно. Такие отношения часто обозначаются символом ≤. Аксиомы частичного порядка могут быть записаны тогда привычным способом:

P1. x ≤ x для всех x S.

P2. Если x ≤ y и y ≤ x, то x = y. P3. Если x ≤ y и y ≤ z, то x ≤ z.

Пр и м е р 7. Отношение m|n (m делит n) является частичным упорядочением на множестве всех положительных целых чисел.

Пр и м е р 8. Обычное отношение ≤ является частичным упорядочением множества всех положительных целых чисел.

Пр и м е р 9. Для любого множества U отношение S T является частичным порядком на множестве P (U ) всех подмножеств множества U .

Оп р е д е л е н и е 16. Частично упорядоченным множеством называется любая пара [S, ≤], где ≤ частичный порядок

намножестве S.

Имеется много полезных примеров частичных упорядочений. Рассмотрим некотоpые из простейших свойств частично упорядоченных множеств. Во-первых, отношение, обратное к частичному порядку ≤, снова является частичным порядком, который называется двойственным к первому и обозначается символом ≥. Таким образом, по определению, X ≥ Y тогда и только тогда, когда Y ≤ X. Во-вторых, частично упорядоченные множества, состоящие из небольшого числа элементов, удобно описывать диаграммами. Маленькие кружочки на них означают элементы; линия, ведущая вверх, соединяет элемент с каждым непосредственно

25

следующим за ним большим элементом.

П р и н ц и п д в о й с т в е н н о с т и. Мы уже упоминали, что обращение частичного порядка является частичным порядком. Поэтому в любой общей теореме о частично упорядоченных множествах можно всюду заменить отношение ≤ отношением ≥, не нарушив ее истинности. Эта математическая теорема о теоремах называется принципом двойственности в теории частично упорядоченных множеств.

В частично упорядоченном множестве [P (3), ] элементы и 3 являются универсальными границами потому, что ≤ x ≤ 3 для любого элемента x P (3). Это понятие можно определить в обшем случае: элементы O и I называются универсальными границами частично упорядоченного множества S (соответственно верхней и нижней), если

Иными словами, O наименьший, а I наибольший элемент множества S.

Лемма 2. В любом частично упорядоченном множествые [S, ≤] может существовать не более одного наименьшего эле-

мента и не более одного наибольшего элемента.

Д о к а з а т е л ь с т в о. Пусть O, O два наименьших элемента [S, ≤]. Тогда O ≤ O (ибо O наименьший элемент) и O ≤ O (ибо O наименьший элемент). Согласно P2 отсюда следует, что O = O . Доказательство для I аналогично.

Cуществуют частично упорядоченные множества без универсальных границ. Таково множество вещественных чисел [R, ≤] с обычным отношением порядка (если оно не расширено формальным присоединением –∞, ∞).

Кроме того, [R, ≤] является линейно упорядоченным множеством или цепью: кроме свойств P1–P3, оно обладает свойством P4. Для любых x, y либо x ≤ y, либо y ≤ x.

Всякое подмножество упорядоченного множества, очевидно, само упорядочено индуцированным на нем бинарным отношением. Если множество линейно упорядочено, то его подмножества также линейно упорядочены. Все это следует из того, что свойства P1, P2, P3, P4 наследственны, т. е. сохраняются при ограничении на любое подмножество своей области, если они выполнялись на всей области.

26

Д о м и н и р о в а н и е. С любым отношением частичного порядка ≤ свзан ряд других бинарных отношений. К ним относятся: отношение x < y, означающее, что x ≤ y, но x =6 y; отношение x > y, означающее, что y < x, а так же отношение x y (««x и y не сравнимы»»), означающее, что ни одно из двух утверждений x ≤ y и y ≤ x неверно. Ясно, что если x, y [S, ≤], то справедлива только одна из следующих альтернатив: x = y, x > y, x < y или x y. Менее очевидно отношение, связанное с ≤, а именно доминирование.

О п р е д е л е н и е 17. Пусть P = [S, ≤] частично упорядоченное множество , а a и b его элементы. Будем говорить, что a доминирует над b, если a > b, но ни для какого x S неверно,

что a > x > b.

Покажем, что отношение ≤ однозначно восстанавливается по отношению доминирования в любом конечном частично упорядоченном множестве.

Теорема 6. Пусть a < b в конечном частично упоядоченном множестве P . Тогда P содержит по крайней мере одну цепь xo = a < x1 < ... < xl = b, в которой каждый из элементов xi (i =

1, . . . , l) доминирует над xi−1.

Д о к а з а т е л ь с т в о. используем индукцию по количеству n элементов y со свойством a < y < b. Если n = 0, то b доминирует над a, и утверждение очевидно. Пусть n > 0, и a < c < b. Тогда количество элементов y, удовлетворяющих условию a < y < c, и элементов z, удовлетворяющих условию c < z < b, не превосходит n − 1, ибо c мы исключили. Значит, по предположению индукции существуют конечные цепи, связывающие a с c и c с b, соседние элементы которых находятся в отношении доминирования. Соединяя эти две цепи, получим требуемый результат.

Удобно представить себе, что если a доминирует над b, то b находится в прямом подчинении к a относительно некоторой иерархии. Тогда x ≤ y означает отношение подчинения.

О п р е д е л е н и е 18. Элемент m частично упорядоченного множества [S, ≤] называется минимальным, если не существует такого элемента x S, что x < m. Элемент m называется максимальным, если не существует такого элемента x S, что x > m.

Напомним, что x < m означает, x ≤ m, но x =6 m; x > m означает, что m ≤ x, но m =6 x.

Очевидно, что если частично упорядоченное множество облада-

27

ет универсальной нижней границей, или наименьшим элементом O, то O является единственным минимальным элементом. В неупорядоченном множестве (где x ≤ y означает x = y) любой элемент минимален, а так же максимален. В цепи минимальный элемент должен быть наименьшим, и поэтому он единствен.

Следующий принцип, относящийся к конечным частично упорядоченным множествам, играет важную роль. Он утверждает существование согласованной (с порядком) нумерации.

Теорема 7. Пусть [S, ≤], S = {s1, . . . , sn} конечное частично упорядоченное множество. Тогда элементы S можно занумеровать таким образом: S = {x1, . . . , xn}, что из xi < xj будет следовать i < j.

Д о к а з а т е л ь с т в о. Положим Xm = {s1, . . . , sn}, где первоначальная нумерация S = {s1 , . . . , sn} выбрана каким угодно

способом. Мы построим последовательность биекций βm множеств

будет удовлетворять сформулированному в теореме утверждению:

При m = 1 биекция β1 строится однозначно. Предположим, что биекция βn−1 : n – 1 → n – 1 с требуемым свойством уже построена. Обозначим через k наименьшее из чисел i, обладающих

тельно, и здесь i < k (случай i = k невозможен); доказательство завершено.

28

Следствие. В любом конечном частично упорядоченном множестве P есть минимальный элемент m: не существует x P , такого, что x < m.

В е р х н я я и н и ж н я я г р а н и. Пусть S некоторое подмножество частично упорядоченного множества P . Назовем a P нижней границей, или минорантой, множества S, если a ≤ x для всех x S. Назовем a верхней границей, или мажорантой, множества S, если a ≥ x для всех x S. Назовем элемент b P нижней гранью S, если

множества имеет не более одной верхней и не более одной нижней грани.

Д о к а з а т е л ь с т в о. Пусть b1, b2 нижние грани множества S. Тогда b1 ≤ b2, потому что b1 нижняя граница, а b2 наибольшая нижняя граница. Аналогично, b2 ≤ b1. Из свойства P2 следует, что b1 = b2. Двойственное рассуждение доказывает единственность верхней грани.

2.5.Графы

Оп р е д е л е н и е 19. Kонечным графом G = (X, α) называется пара, где X конечное множество вершин, а α — бинарное

отношение на X.

Если α — симметричное отношение, то G называется неориентированным графом. В противном случае — ориентированным.

Если вершины x и y из X находятся в отношении α, то пишут xαy и говорят, что они смежны, а связь между x и y осуществляется с помощью ребра, ориентированного от x к y. Ребро, соответствующее соотношению xαx, называется петлей.

П р и м е р 7. Пусть X = {1, 2, 3, 4, 5}, α задается с помощью

29

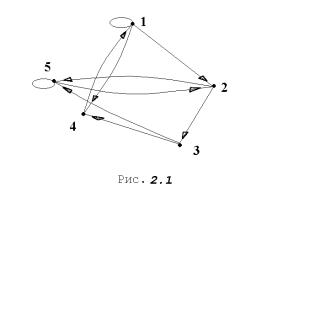
графика следующим образом:

G(α) = {(1, 1)(1, 2)(1, 4)(4, 1)(2, 3)(2, 5)(5, 2)(3, 4)(3, 5)(5, 5)}.

Графическое изображение этого графа имеет вид, указанный на рисунке.

Каждому бинарному отношению на X отвечает матрица отношений. Следовательно, с каждым графом можно связать матрицу из нулей и единиц ||aij ||, называемую матрицей смежности, такую, что

1 если xiαxj , aij = 0 если xiα′ xj .

О п р е д е л е н и е 20. Два графа G = (X, α) и H = (Y, β)

называются изомофными, если существует биекция ϕ : X → Y, такая, что для всех x, y X и z, t Y , для которых ϕ(x) = z, ϕ(y) = t, из того, что xαy в G, следует zβt в H.

П р и м е р 8. Пусть G = (X, α) и H = (Y, P ), такие, что

X = {1, 2, 3}, Y = {a, b, c}

и

G(α) = {(1, 2)(2, 3)(3, 1)}, G(β) = {(a, c)(c, b)(b, a)}.

(aβc), (2α3) → (cβb), (3α1) → (bβa) при отображении ϕ. Однако, биекция ϕ : 1 → a, 2 → b, 3 → c не является изоморфизмом, так как из того, что 1α2 и ϕ(1) = a, ϕ(2) = b, следует, что (1, 2) → (a, b), а это не удовлетворяет определению изоморфизма, так как a и b не находятся в отношении β, т. е. aβ′b.

30