Книги и конспекты / Горьковой Дискретная Математика

П р и м е р 17. Пусть даны графы G = (X, F ) и H = (Y, P ), где X = {x1, x2}, Y = {y1, y2, y3}, а F и P задаются следующими таблицами:

Согласно определению

Q = G × H = (Z, U )

и

Z = {(x1, y1)(x1, y2)(x1, y3)(x2, y1)(x2, y2)(x2, y3)},

Введем обозначения:

(x1, y1) = 1, (x1, y2) = 2, (x1, y3) = 3,

(x2, y1) = 4, (x2, y2) = 5, (x2, y3) = 6,

тогда Z = {1, 2, 3, 4, 5, 6}.

Для вычисления представлений для графов G и H необходимо вычислить графы G и H . В нашем случае они имеют вид

Очевидно,

TZ = TX • TY = {(2, 2)1, (1, 2)2, (2, 1)3, (4, 4)4, (2, 4)5, (4, 2)6}

. Тогда

AU (2, 2)1 = AF (1, 1)x1 • AP (2, 2)y1 = (2, 2)x2 • {(2, 2)y1 , (2, 1)y3 } = {(4, 4)4, (4, 2)6},

AU (1, 2)2 = AF (1, 1)x1 • AP (1, 2)y2 = (2, 2)x2 • (1, 2)y2 = (2, 4)5

AU (2, 1)3 = AF (1, 1)x1 • AP (2, 1)y3 = (2, 2)x2 • {(2, 2)y1 , (1, 2)y2 } = {(4, 4)4, (2, 4)5},

AU (4, 4)4 = AF (2, 2)x2 • AP (2, 2)y1 = {(1, 1)x1 , (2, 2)x2 } • {(2, 2)y1 , (2, 1)y3 } = {(2, 2)1, (2, 1)3, (4, 4)4, (4, 2)6},

AU (2, 4)5 = AF (2, 2)x2 • AP (1, 2)y2 = {(1, 1)x1 , (2, 2)x2 } • (1, 2)y2 = {(1, 2)2, (2, 4)5},

71

Теорема 26. Представление графа N = (Z, L) = G + H есть пара ΠN = (TZ , AL), такая, что TZ = TX + TY , где TZ есть множество всевозможных сумм пар из TX и TY , определенных следующим образом:

ξ= |F x × {y}| + |{x} × P y| = |F x| + |P y|,

η= |F −1x × {y}| + |{x} × P −1y| = |F −1x| + |P −1y|,

и если |F x| = α, |F −1x| = β, |P y| = γ, |P −1y| = δ, то ξ = α + γ, η = β + δ.

Пусть x F x и y P y, тогда

ξ = |F x × {y}| + |{x} × P y| − |(F x × {y}) ∩ ({x} × P y)| =

= |F x| + |P y| − 1 = α + γ − 1.

Аналогично η = β + δ − 1.

Пусть (ξ, η)z = (α, β)x + (γ, δ)y = (α + γ − t, β + δ − t)z , где t = 1

при x F x, y P y и t = 0 во всех остальных случаях. Из определения представления следует, что

72

AL(ξ, η)z = {(ξ′, η′)z′ }z′ N z=F x×{y} {x}×P y = = {(ξ′, η′)z′ }z′ F x×{y} {(ξ′, η′)z‘}z′ {x}×P y .

Так как прямому произведению X ×Y в представлении для суммы графов соответствует TX +TY , то из того, что F x X, {y} Y следует, что прямому произведению F x × {y} будет отвечать TF x + T{y}. Аналогично прямому произведению {x} × P y отвечает T{x} + TP y . Таким образом:

{(ξ′, η′)z′ }z′ F x×{y} = TF x + T{y} = {(α′, β′)x′ }x′ F x + (γ, δ)y =

= AF (α, β)x + (γ, δ)y ,

а

{(ξ′, η′)z′ }z′ {x}×P y = T{x} + TP y = (α, β)x + {(γ′, δ′)y′ }y′ P y =

= (α, β)x + AP (γ, δ)y

. З а м е ч а н и е. Следует отметить, что в случае, когда F x = F −1x = , очевидно, должно быть (0, 0)x + (γ, δ)y = (γ, δ)z , если положить | | = 0.

П р и м е р 18. Для графов G = (X, F ) и H = (Y, P ) из примера 17 построим представление ΠN = (TZ , AL) графа N = (Z, L) = G + H. В данном случае имеем

TZ = TX + TY = {(3, 3)1, (2, 3)2, (3, 2)3, (3, 3)4, (2, 3)5, (4, 3)6}.

Вычислим образы каждого элемента из TZ .

AL(3, 3)1 = AF (1, 1)x1 + (2, 2)y1 (1, 1)x1 + AP (2, 2)y1 = (2, 2)x2 + (2, 2)y1 (1, 1)x1 + {(2, 2)y1 , (2, 1)y3 } = {(3, 3)4, (3, 3)1, (3, 2)3},

AL(2, 3)2 = AF (1, 1)x1 + (1, 2)y2 (1, 1)x1 + AP (1, 2)y2 = (2, 2)x2 + (1, 2)y2 (1, 1)x1 + (1, 2)y2 = {(2, 3)5, (2, 3)2},

AL(3, 2)3 = AF (1, 1)x1 + (2, 1)y3 (1, 1)x1 + AP (2, 1)y3 = (2, 2)x2 + (2, 1)y3 (1, 1)x1 + {(2, 2)y1 , (1, 2)y2 } = {(4, 3)6, (3, 3)1, (2, 3)2},

AL(3, 3)4 = AF (2, 2)x2 + (2, 2)y1 (2, 2)x2 + {(2, 2)y1 , (2, 1)y3 } = {(1, 1)x1 , (2, 2)x2 } + (2, 2)y1 (2, 2)x2 + {(2, 2)y1 , (2, 1)y3 } =

= {(3, 3)1, (3, 3)4, (4, 3)6},

AL(2, 3)5 = AF (2, 2)x2 + (1, 2)y2 (2, 2)x1 + AP (1, 2)y2 = {(1, 1)x1 , (2, 2)x2 } + (1, 2)y2 (2, 2)x2 + (1, 2)y2 = {(2, 3)2, (2, 3)5},

73

Теорема 27. Представление графа K = (Z, R) = G H есть пара ΠK = (TZ , AR), такая, что TZ = TX TY , где TZ — множество всевозможных композиций пар из TX и TY , определенных следующим образом: если (α, β)x TX , (γ, δ)y TY , то (α, β)x

(γ, δ)y = (αl+γk−αγ, βl+δk−βδ)z , k = |X|, l = |Y |, а AR : TZ → TZ таково, что AR(ξ, η)z = {(AF (α, β)x TY ) (TX AR(γ, δ)y )}, где

(ξ, η)z = (α, β)x (γ, δ)y , z = (x, y) Z, x X, y Y .

Д о к а з а т е л ь с т в о. Действительно, по определению

ξ = |(F x ×Y ) (X ×P y)| = |F x||Y |+ |X||P y|− |(F x ×Y ) ∩(X ×

t1 = |F x × P y ∩ F x × P y| = |F x × P y| = αγ.

Аналогично вычисляется величина t2:

t2 = |F −1x × Y ∩ X × P −1y| = βδ.

Таким образом, ξ = αl + γk − αγ, η = βl + δk − βδ.

Пусть

74

(ξ, η)z = (α, β)x (γ, δ)y = (αl + γk − αγ, βl + δk − βδ)z . Тогда

AR(ξ, η)z = {(ξ′, η′)z′ }z′ F x×Y X×P y =

= {(ξ′, η′)z′ }z′ F x×Y {(ξ′, η′)z′ }z′ X×P y

Так как декартову произведению X × Y в прдставлении композиции графов G и H соответствует TX TY , то декартову произведению F x × Y будет соответствовать TF x TY , а декартову произведению X × P y — TX TP y .

Но

TX = {(α, β)x}x X ; TY = {(γ, δ)y }y Y ,

TF x = {(α′, β′)x′ }x′ F x, TP y = {(γ′, δ′)y′ }y′ P y .

Следовательно,

AP (ξ, η)z = TF x TY TX TP y = AF (α, β)x TY TX AP (γ, δ)y ,

где

(ξ, η)z = (α, β)x (γ, δ)y , z = (x, y) Z, x X, y Y .

П р и м е р 19. Для графов G = (X, F ) и H = (Y, P ) из примера

17вычислим представление ΠM = (TZ , AS ) графа M = (Z, S).

Из теоремы о представлении композиции представлений следу-

ет, что

TZ = TX TY = {(5, 5)1, (4, 5)2, (5, 4)3, (6, 6)4, (6, 6)5, (6, 6)6}

AS (5, 5)1 = AF (1, 1)x1 {(2, 2)y1 , (1, 2)y2 , (2, 1)y3 } {(1, 1)x1 , (2, 2)x2 } AP (2, 2)y1 = (2, 2)x2 {(2, 2)y1 , (1, 2)y2 , (2, 1)y3 } {(1, 1)x1 , (2, 2)x2 } {(2, 2)y1 , (2, 1)y3 } = {(6, 6)4, (6, 6)5, (6, 6)6, (5, 5)1, (5, 4)3},

AS (4, 5)2 = AF (1, 1)x1 {(2, 2)y1 , (1, 2)y2 , (2, 1)y3 } {(1, 1)x1 , (2, 2)x2 } AP (1, 2)y2 = (2, 2)x2 {(2, 2)y1 , (1, 2)y2 , (2, 1)y3 } {(1, 1)x1 , (2, 2)x2 } (1, 2)y2 = {(6, 6)4, (6, 6)5, (6, 6)6, (4, 5)2},

AS (5, 4)3 = AF (1, 1)x1 {(2, 2)y1 , (1, 2)y2 , (2, 1)y3 } {(1, 1)x1 , (2, 2)x2 } AP (2, 1)y3 = (2, 2)x2 {(2, 2)y1 , (1, 2)y2 , (2, 1)y3 } {(1, 1)x1 , (2, 2)x2 } {(2, 2)y1 , (1, 2)y2 } = {(6, 6)4, (6, 6)5, (6, 6)6, (5, 5)1, (4, 5)2},

AS (6, 6)4 = AF (2, 2)x2 {(2, 2)y1 , (1, 2)y2 , (2, 1)y3 } {(1, 1)x1 , (2, 2)x2 }

AP (2, 2)y1 = TX TY = TZ , AS (6, 6)5 = AS (6, 6)6 = TZ .

Таким образом, представление ΠM = (TZ , AS ) для композиции M = (Z, S) имеет вид

75

Пусть N — некоторое подмножество из X, а M — из Y и пусть заданы два графа Бержа G = (X, F ), H = (Y, P ).

Пусть (F x, N) #(M, P y) = (F x × M) (N × P y), x X, y Y .

Очевидно, при различных N и M операция # является одной из рассмотренных ранее операций из A= {×, +, }. Действительно, при N = , M = P y операция # есть ×; при N = {x}, M = {y} # есть +, а при N = X, M = Y # есть .

Таким образом, рассмотренные операции на графах можно обобщить, заменив их операцией # .

Будем говорить, что граф V = (Z, B) получается из графов G и H с помощью операции # , и писать V = G# H, если Z = X × Y

и Bz = (F x, N)#(M, P y).

По аналогии с графами можно обобщить все операции над представлениями, поставив в соответствие операции # над графами операцию ♯ над представлениями, при различных ситуациях совпадающую с одной из рассмотренных операций над представлениями.

Теорема 28. Представление графа V = (Z, B) = G#H есть

(ξ, η)z = (α, β)x♦(γ, δ)y = (αn + γm − p1, βn + δm − p2)z ,

а AB : TZ → TZ на элементах из TZ определяется следующим образом

AB (ξ, η)z = (AF (α, β)x, TN )♯(TM , AP (γ, δ)y ) =

=(AF (α, β)x♦TM ) (TN ♦AP (γ, δ)y ).

Вэтом случае будем писать

ΠV = ΠG♯ΠH ; ΠG = (TX , AF ); ΠH = (TY , AP ).

76

Д о к а з а т е л ь с т в о. Действительно, если n = m = 0, −p1 = αγ, −p2 = βδ, то мы имеем дело с теоремой 25; при n = l, m = k, p1 = αγ, p2 = βδ — это есть теорема 27; при m = n = 1, p1 = p2 = 0 1 мы имеем дело с теоремой 26.

77

5

МИНИМАЛЬНЫЕ РАСКРАСКИ

ИКРИТИЧЕСКИЕ ГРАФЫ

5.1.Основные понятия и определения

Здесь мы будем иметь дело с так называемыми обыкновенными графами, т. е. неориенированными графами без петель и кратных ребер.

Вершинной раскраской графа [4] называется такое приписывание цветов его вершинам, что никакие две смежные вершины не окрашиваются в один цвет.

Дадим другое определение раскраски, более формальное.

О п р е д е л е н и е 47. Раскраской графа G = (X, F ) в m цветов, или m-раскраской, называется разбиение его вершин X на классы C1, C2 , ..., Cm попарно несмежных вершин.

Классы Ci называются одноцветными классами. Хроматическое число χ(G) графа G определяется

как наименьшее m, для которого граф G имеет m- раскраску.

Граф G называется m-раскрашиваемым, если χ(G) ≤ m, и m-хpоматическим, если χ(G) = m.

Хроматическое число для некоторых простых графов легко вычисляется. Если Fm — полный m- вершинный граф, то χ(Fm) = m, χ(Ck ) = 3, где Ck —

77

простой цикл нечетной длины k, χ(C2n) = 2 [4]. Интересной в теоретическом плане и важной для

приложений является следующая задача. По данному графу установить, в какое число цветов он окрашивается.

Среди n-хроматических графов выделяются минимальные по числу вершин.

О п р е д е л е н и е 48. Граф G называется критическим, если χ(G−x) < χ(G) для любой вершины x; если при этом χ(G) = m, то граф G называется m- критическим.

Очевидно, что если G — критический граф, то χ(G) − 1 = χ(G − x) для каждой его вершины x .

Единственный 2-критический граф — это F2. Все 3- критические графы исчерпываются простыми циклами нечетной длины.

Каждый m-хроматический граф содержит m-критический подграф. Действительно, если H — такой наименьший порожденный [5] подграф графа G, что χ(H) = χ(G),

то H — критический граф.

Очевидно, каждый критический граф связен.

Если Fp = (X, F ) — полный граф, то для любого Y X справедливо равенство χ(Fp − Y ) = p − |Y | и, следовательно, граф Fp критический.

Для любого другого m-критического графа, m > 2, нельзя удалить не менее двух вершин, не уменьшая при этом хроматическое число больше, чем на единицу.

Действительно, если C — произвольное подмножество любого одноцветного класса, то χ(G − C) = m − 1. Но, если x и y — любые две вершины m-критического неполного графа, то не всегда их удаление уменьшает

78

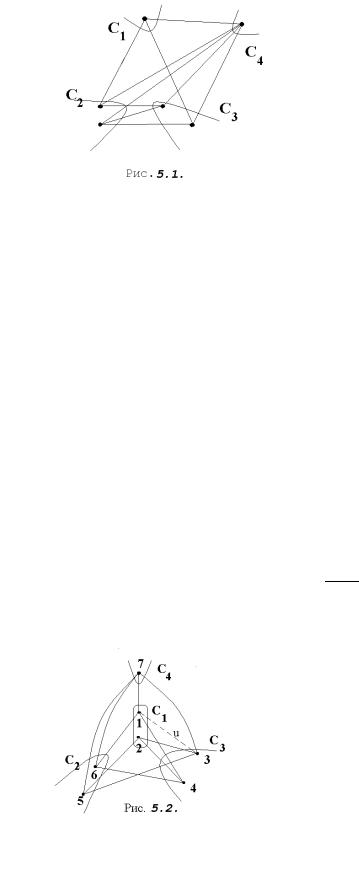
хроматическое число на единицу. Следующий пример служит тому подтверждением.

Критический граф может обладать еще одним свойством: χ(G − u) = χ(G) − 1 для любого ребра u графа G. В этом случае граф G называется ребернокритическим. При χ(G) = n граф G называется n- реберно-критическим.

Каждый реберно-критический граф является критическим, обратное неверно. Например, граф G, минимальная раскраска которого представлена на рис. 5.1, является 4-критическим, но не реберно-критическим, поскольку χ(G − u) = 4.

Таким образом, реберно-критические графы обладают всеми свойствами критических графов.

Пусть G = (X, F ) — m-критический граф, X — множество вершин, а F : X → X — отображение, ставящее в соответствие вершине x X множество смежных с ней вершин F x. Пусть π(m) = (C1, C2, ..., Cm ) — его минимальная вершинная раскраска, где Ci, i = 1, m, — классы одноцветных вершин.

79