3.7.5. Силы, действующие в червячном зацеплении

Возникающую при работе червячной передачи силу нормального давления между зубьями колеса и витками резьбы червяка считают приложенной в полюсе зацепления. Разложив это нормальное (полное) усилие по трем взаимно перпендикулярным направлениям, можно найти осевое, окружное и радиальное усилия, действующие в червячном зацеплении (рис. 34).

Окружное усилие на червячном колесе равно осевому усилию на червяке

где — крутящий момент на червячном колесе,

— диаметр начальной окружности червячного колеса.

Окружное усилие на червяке равно осевому усилию на червячном колесе:

где — крутящий момент на червяке;

— диаметр начальной окружности червяка;

— угол подъема винтовой линии на червяке;

— угол трения.

Радиальное (распорное) усилие, раздвигающее червяк и колесо

.

3.7.6. Расчет на изгиб зубьев червячного колеса

Червячные передачи рассчитываются на прочность по напряжениям изгиба и по контактным напряжениям. Как правило, прочность на изгиб не определяет размеров передачи и расчет на изгиб применяется в качестве проверочного.

В связи с тем, что условия зацепления и несущая способность передач с цилиндрическими червяками очень близки, расчеты выполненные для архимедова червяка справедливы и для червяков других типов.

Ширина ( ) колеса по дуге окружности равна:

,

Длина контактных линий (по аналогии с косозубыми):

,

где — торцовый коэффициент перекрытия .

Длина контактных линий в среднем равна

.

Тангенциальная и нормальная нагрузки на единицу длины контактных линий:

, ,

где — окружное усилие на колесе.

К — коэффициент нагрузки .

Принято

Расчет на изгиб ведут по колесу, т. к. витки червяка значительно прочнее. Расчет производится в форме проверочного по номинальным напряжениям

,

если принять , (m — осевой, стандартный модуль).

Заменить его значением через и , то после преобразования получим

,

где и — нормальный и осевой модуль червяка;

— коэффициент прочности зубьев для червячных колес ( ),

выбирается по эквивалентному числу зубьев ;

— допускаемое номинальное напряжение изгиба, .

3.7.7. Расчет червячной передачи на контактную прочность

Аналогично расчету зубчатых передач за исходную принимают формулу Герца

,

где — приведенный модуль упругости материала

,

где — модуль упругости материала червяка;

— модуль упругости материала колеса;

— приведенный радиус кривизны.

Витки архимедова червяка в осевом сечении имеют профиль прямобочной рейки с , а зубья червячного колеса имеют эвольвентный профиль. Поэтому расчетный приведенный радиус кривизны равен радиусу кривизны зуба червячного колеса в полюсе зацепления, т. е.

.

Подставив в формулу значения ; ; ; ; ; ; .

, (бронза и чугун), после преобразований получим

.

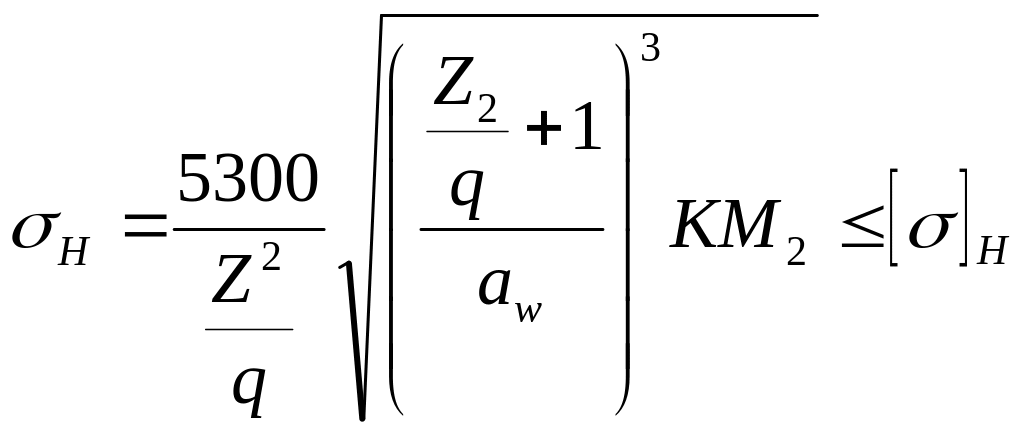Если выразить через d₂ и d₁ (уменьшить числитель и знаменатель на ), то после ряда преобразований получим:

.

При проектировании новых передач необходимо рассчитать межосевое расстояние , см

,

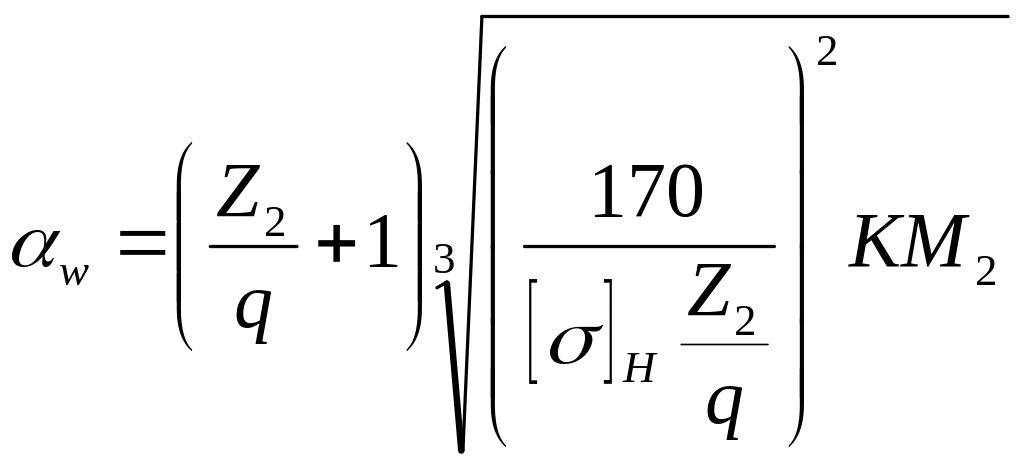где — допускаемые контактные напряжения для колеса, ;

— крутящий момент на колесе, .