3.6.7. Расчет основных геометрических параметров цилиндрических прямозубых колес

Эвольвентное зацепление двух зубчатых колес характеризуется следующим параметрами (ГОСТ 16530-70) (см. рис. 21).

НАЧАЛЬНЫЕ ОКРУЖНОСТИ ( и ) — воображаемые окружности, которые в процессе работы передачи перекатываются одна по другой без скольжения. Начальные окружности появляются у зубчатых колес в собранной передаче. Для отдельно взятого колеса понятие начальной окружности отсутствует. Оно имеет делительную окружность.

ОКРУЖНОСТЬ ВЕРШИН ЗУБЬЕВ ( ) — окружность ограничивающая головки зубьев.

ОКРУЖНОСТЬ ВПАДИН ( ) — окружность, проходящая через основания впадин зубьев.

ОСНОВНАЯ ОКРУЖНОСТЬ ( и ) — окружность, при развертке которой получается эвольвента.

ДЕЛИТЕЛЬНАЯ ОКРУЖНОСТЬ ( и ) — окружность зубчатого колеса, по которой обкатывается делительная окружность (прямая) инструмента в процессе нарезания зубьев. Делительная окружность колеса является начальной только в процессе изготовления (нарезания) зубьев. У некорригированных колес и при высотной коррекции начальные и делительные окружности совпадают.

Рис. 21. Элементы зубчатого зацепления

ПОЛЮС ЗАЦЕПЛЕНИЯ (точка ) — точка касания начальных окружностей.

ОКРУЖНОЙ ШАГ ЗАЦЕПЛЕНИЯ ( ) — расстояние между одноименными профилями, измеренное по дуге делительной окружности, зубчатого колеса.

ГОЛОВКА ЗУБА ( ) — часть зуба между делительной окружностью зубчатого колеса и его окружностью вершин зубьев.

НОЖКА ЗУБА ( ) — часть зуба между делительной окружностью и его окружностью впадин.

ВЫСОТА ЗУБА ( ) равна сумме высот головки и ножки зуба.

ДУГА ЗАЦЕПЛЕНИЯ ( ) — путь по начальной окружности, проходимой точкой профиля за время зацепления пары сопряженных зубьев.

КОЭФФИЦИЕНТ ПЕРЕКРЫТИЯ ( ) — отношение дуги зацепления к окружному шагу.

ЛИНИЯ ЗАЦЕПЛЕНИЯ ( и ) — линия, по которой перемещается точка касания зубьев. Линия зацепления проходит через полюс зацепления и является касательной к основным окружностям.

УГОЛ ЗАЦЕПЛЕНИЯ ( ) — угол между линией зацепления и касательной к начальным окружностям в полюсе зацепления.

Все модули стандартизованы в пределах от 0,05 мм до 100 мм.

Рассмотренные параметры составляют определенные кинематические зависимости. В таблице 2 приводятся основные соотношения для цилиндрических некорригированных зубчатых передач внешнего зацепления.

Таблица 2

Параметры зацепления	Формулы
Окружной модуль
Нормальный модуль
Нормальный шаг
Межосевое расстояние
Высота головки зуба
Высота ножки зуба
Высота зуба
Радиальный зазор
Делительный диаметр
Начальный диаметр
Диаметр основной окружности
Диаметр вершин зубьев
Диаметр впадин
Коэффициент перекрытия

3.6.8. Расчет зубьев цилиндрических прямозубых зубчатых колес на изгиб

При этом зуб рассматривают как балку, защемленную одним концом и нагруженную силой . Такое положение нагрузки принимается как наиболее опасное. За опасное сечение его у корня в зоне наибольшей концентрации напряжений. Максимальное напряжение возникает на стороне сжатия (нерабочая сторона), но расчет производится по напряжению на рабочей стороне, т. к. усталостная трещина возникает на растянутой стороне зубьев.

- Расчеты приближены по форме к расчетам, рекомендуемым ИСО и СЭВ.

- Коэффициенты общие для расчетов на изгиб и на контактную прочность обозначены буквой , специфические коэффициенты для расчета на изгиб – буквой , а для расчета на контактную прочность – .

- Для обозначения расчета на изгиб, который проводится по ножке зуба принят индекс (от термина ножка – Fut – на английском и немецком языках).

- Для обозначений расчета на контактную прочность принят индекс , в честь автора теории расчетов контактных напряжений Г. Герца.

Расчет ведется по расчетной окружной силе , отнесенной к единице ширины венца.

,

где: — передаваемое окружное усилие;

— ширина венца зубчатого колеса (длина зуба);

— коэффициент нагрузки, учитывающий дополнительные вредные явления (удары).

— расчетная окружная сила, отнесенная к единице ширины венца .

Нормальная удельная сила равна:

,

где — нормальная удельная сила;

— угол зацепления.

Перенесем силу давления вдоль линии ее действия (линия зацепления) в точку, расположенную на оси симметрии зуба и разложим на две составляющие (рис. 22): изгибающую зуб , вызывающую в опасном сечении напряжения изгиба и сжимающую зуб , вызывающую в зубе напряжения сжатия . Угол несколько больше угла профиля ( ).

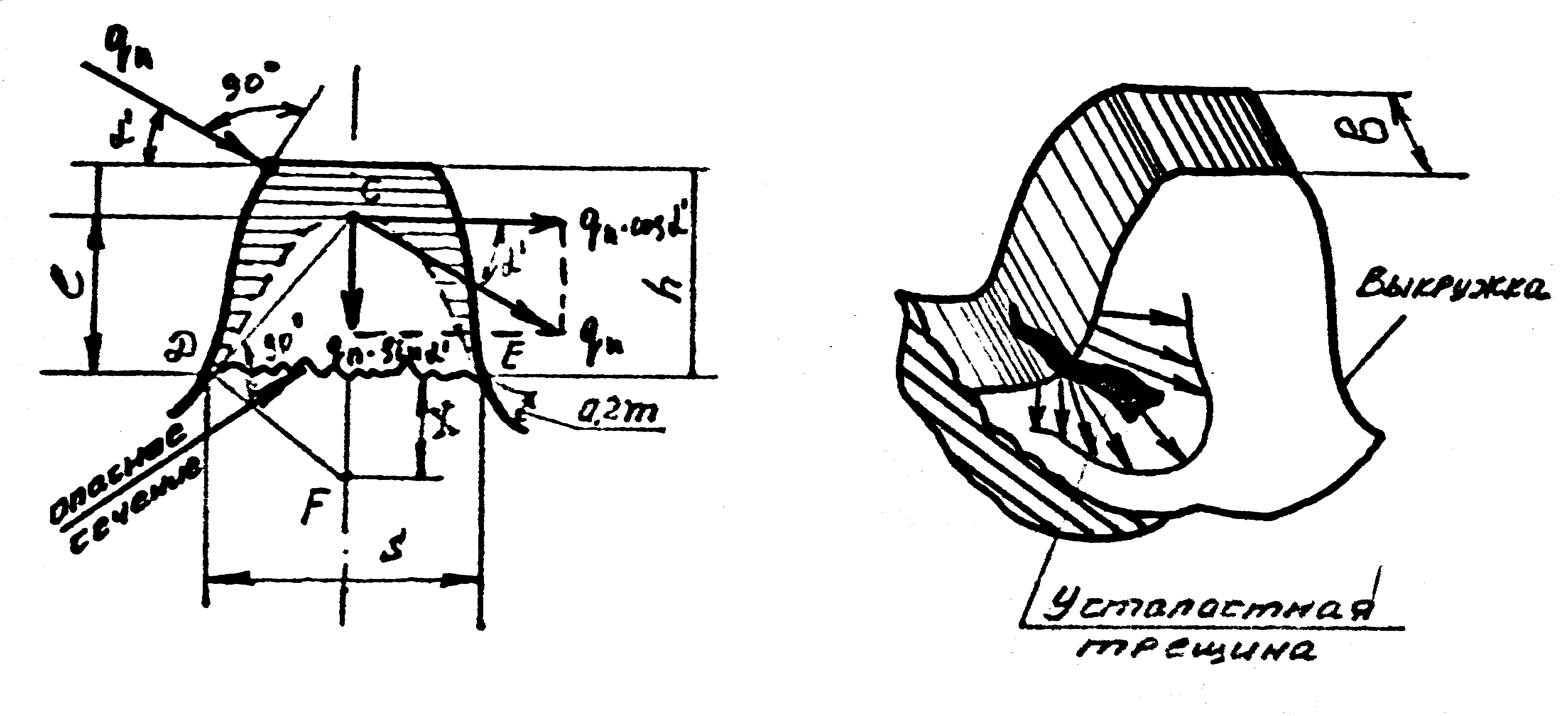
Рис. 22. Схема расчета зубьев на изгиб

Номинальное напряжение в опасном сечении:

,

где — номинальное напряжение;

— напряжение на изгиб

— напряжение на сжатие;

; ; ;

где — изгибающий момент;

— момент сопротивления на изгиб опасного сечения;

— расчетное плечо силы;

— толщина зуба в опасном сечении;

тогда:

;

;

.

Умножим числитель и знаменатель на модуль и заменим получим:

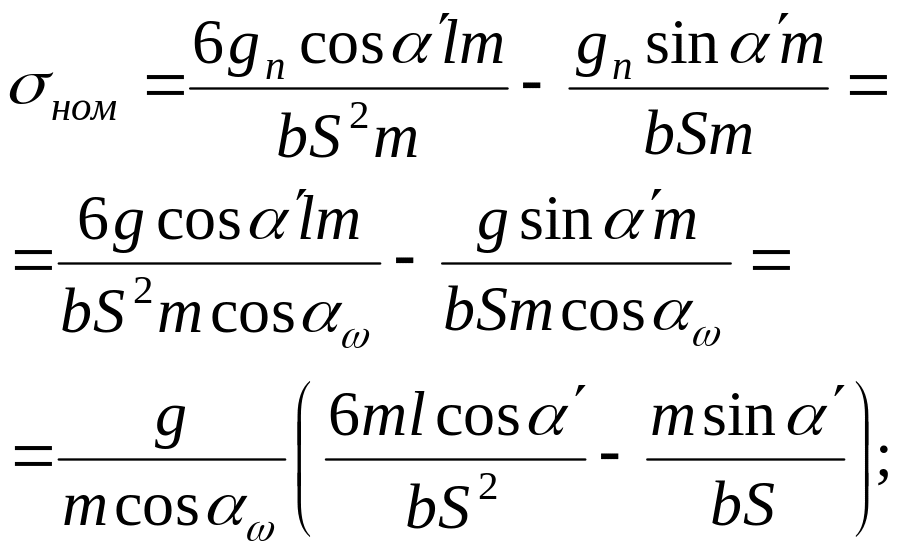
приняв:

;

получим:

.

Местные напряжения:

;

обозначив получим:

,

где — теоретический коэффициент концентрации напряжений;

и — коэффициенты прочности зубьев соответственно по номинальным и местным напряжениям;

— представляет собой номинальное напряжение в опасном сечении зуба при и ;

— местное напряжение при тех же условиях.

Технические расчеты удобно вести по формулам, в которых условия нагружения заданы в форме номинальных крутящих моментов ( ) или мощности ( ), частоты вращения и коэффициента нагрузки .

;

где — номинальный крутящий момент;

— начальный диаметр;

— окружной модуль;

— число зубьев.

Для технических проверочных расчетов следует умножить и приняв получим:

;

если то:

.

Модуль и ширина зубчатого венца, прежде всего, определяют прочность зуба на изгиб. Приняв и решив последнее уравне­ние относительно модуля, после преобразований получим:

,

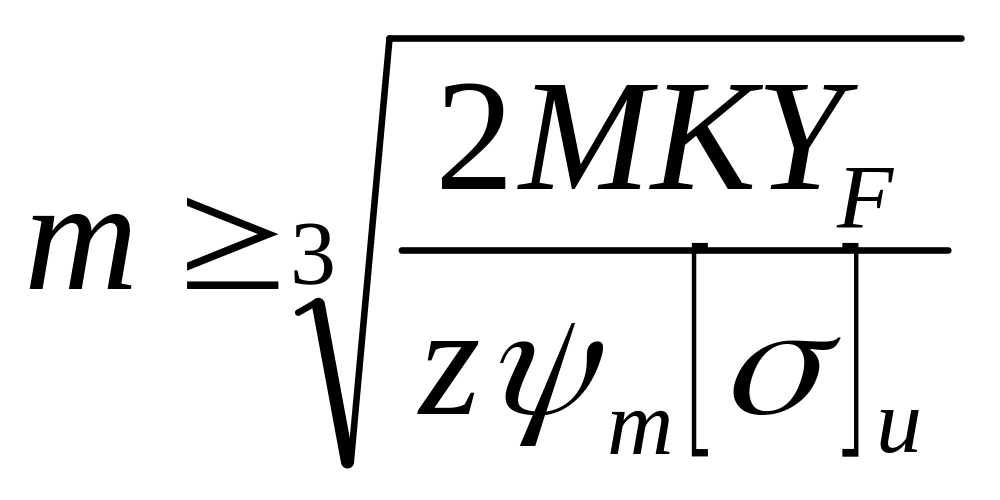где — коэффициент.

Наиболее рациональной формой расчета, обеспечивающей равнопрочностъ зубьев по выкрашиванию и излому, является определение модуля по известному межосевому расстоянию и ширине зубчатого венца полученным из расчета на контактную прочность.

Подставим:

,

где — число зубьев колеса;

— делительный диаметр колеса;

— межосевое расстояние;

— передаточное число.

После преобразования получим:

,

откуда:

.

Для большинства редукторов общего назначения:

;

коэффициент нагрузки К можно выразить:

,

где K_β – коэффициент концентрации нагрузки;

K_v – коэффициент динамичности нагрузки.