7.5. Расчет винтовых пружин кручения

При работе пружины кручения в поперечных сечениях витков возникает момент М, который равен внешнему моменту, закру­чивающему пружину, и вектор которого направлен вдоль оси (см. рис. 38). Если разложить М на составляю­щие, то получим

Так как , то пружины кручения рассчитывают на изгиб, по изгибающему моменту , который приближенно принимают

где — расчетное максимальное напряжение изгиба в попереч­ных сечениях проволоки пружины;

— допускаемое напряжение на изгиб для проволоки пружины, ;

К — коэффициент, учитывающий кривизну витков

.

Диаметр проволоки определяют по формуле

.

Шаг витков пружины равен:

где — зазор между витками

мм.

При данном угле закручивания требуемое число рабочих витков пружины находят:

где — осевой момент инерции сечения проволоки

.

Высота пружины в свободном состояния равна:

,

где - высота одного прицепа пружины.

Длина проволоки для изготовления пружины определяется зависимостью:

.

7.6. Расчет плоских пружин

Плоские пружины получили особенно широкое распространение в приборостроении благодаря простоте изготовления и обеспечения различных упругих характеристик.

Плоские пружины бывают трех основных видов:

ИЗМЕРИТЕЛЬНЫЕ, предназначенные для созданий усилий и противо­действующих моментов,

СИЛОВЫЕ — приводящие в движение или тормозящие и фиксирующие положение деталей,

ПРУЖИНЫ ДЛЯ УПРУГИХ СВЯЗЕЙ, применяемые в тех случаях, когда требуется заменить жесткое соединение элементов прибора под­вижным.

По форме плоские пружины могут быть ПРЯМЫМИ, ИЗОГНУТЫМИ и СПИРАЛЬНЫМИ.

Измерительные и силовые пружины изготавливают из инструмен­тальной и пружинной стали (в виде холоднокатаных лент) различных марок: 50Г, 65Г, У7, У8, У8Г, У8ГА, У9, У9А, У10, У10А, УП, УПА, УГ2, У12А, У13, УТЗА, 60СА, 60С2А, 50ХФА.

Прямые и изогнутые пружины, которые должны обладать хоро­шей электропроводностью и антимагнитностью, изготавливаются из алюминиевой бронзы Бр. А 7. Контактные пружины, а также моментные пружины (волоски), обладающие указанными свойства­ми, изготавливаются из лент, проволоки (ГОСТ 9384-75) и бронз марок Бр. ОФ6, 5-1,5; Бр. ОФ4-0,25 и др. Определенный интерес представляют БИМЕТАЛЛИЧЕСКИЕ пружины. Они изготавливаются в виде двухслойных пластин, слои ко­торых выполняется из разнородных материалов. Соединение слоев производится сваркой или пайкой. Материалы слоев различаются коэффициентами линейного расширения. Один из концов биметаллической пружины закрепляется относительно корпуса прибора, второй — может свободно перемещаться. При нагревании слой пру­жины с большим коэффициентом линейного расширения (активный слой) не может расширяться по прямой, чему мешает второй слой с меньшим коэффициентом линейного расширения (пас­сивный слой) и поэтому вы­нужден изгибаться, вместе с пассивным слоем в сторону последнего. Биметаллическая пружина дает максимальный прогиб , если отноше­ние толщин составляющих слоев обратно пропорционально модулям упругости, т.е.

.

Биметалл, удовлетворяющий этому условию называется

НОРМАЛЬНЫМ .

Прогиб конца нормальной биметаллической пружины при нагреве на равен:

,

(А)

где и — коэффициенты линейного расширения;

— толщина пластины, ;

— длина пластины.

В сечении заделки пружины возникают нормальные напряжения, вызванные изгибом от температурного воздействия. Прогиб конца пружины можно представить как результат действия неко­торой сосредоточенном силы Р, приложенной на свободном конце пружины. Для определения напряжений используем формулы сопрома­та, но условно будем считать пластику монометаллической с приведенным модулем упругости.

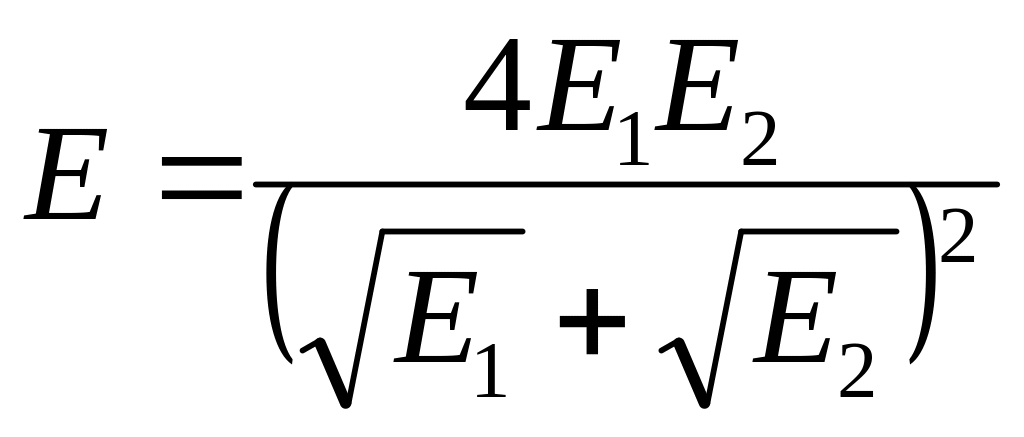
Для балки, заделанной одним концом и нагруженной на конце силой Р, прогиб определяется по формуле:

.

Решая это уравнение совместно с уравнением А (см выше), получим:

.

Искомый эквивалентный изгибающий момент равен:

,

где — момент инерции поперечного (прямоугольного) сечения пружины

.

Небольшие номинальные напряжения в крайних волокнах слоев биме­таллической пружины равны:

активный слой ;

пассивный слой .

Биметаллические пружины разнообразны по форме и чаще приме­няются прямые, изогнутые, спиральные и винтовые.

Биметаллические пружины применяются:

- в регуляторах температуры и релейных устройствах;

• в системах для непосредственного управлений регулирующими органами;

- в качестве температурных компенсаторов;

- в приборах, измеряющих давление, плотность и расход газов;

- в биметаллических амперметрах и ваттметрах.