
Сопротивление материалов. Теория и практика. Воропаев А.А., Попов С.П
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
106 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Вычислим три ординаты у в пролете (при z |
|
|
l |
; |
|
l |
; |
3 |
l ) и две на |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
4 |
|
|
|
|||||
|
|
|
|
|
консоли ( z |
|
|
|
5 |
l; |
3 |
l ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
ql 4 |
|
|
|
|
|
|
|
|
|
|
|
ql 4 |
|
|
|
|
|
|
|
|
|
|
ql 4 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
y |
|
|
l |
0,0046 |
|
|
|
|
; |
|
|
|
y |
|
|
l |
0,0125 |
|
|
; |
y |
|
3 |
|
|
0,015 |
|
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
z |
|
|
|
|
EI x |
|
|
|
|
|
z |
|
|
|
|
EI x |
|
|
z |
l |
|
|
|
EI x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
||||||||||||||||||||
y |
|
|
|
|
0,0413 |
ql |
4 |
|
; y |
|
|
|
|
|
|
0,0925 |
ql 4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
5 |
|
|
EI x |
|
|
3 |
|
|
EI x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
z |
|
l |
|
|
|
|
|
|
|
z |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3. Эпюра прогибов приведена на рис 6.7,г. Упругая линия обращена выпуклостью вниз на участках с положительным изгибающим моментом и выпуклостью вверх там, где изгибающий момент отрицателен. Нулевой точке на эпюре M x соответствует точка перегиба упругой линии.
6.3.4. Расчет статически неопределимых рам Задача. На рис. (6.8) изображена нагруженная в своей плоскости рама,
вертикальные элементы которой имеют момент инерции I, а горизонтальные элементы – k I. Требуется:
1)установить степень статической неопределимости;
2)написать канонические уравнения;
3)построить эпюры М х от единичных сил и от заданной нагрузки;
4)найти перемещения;
5)найти величины «лишних» неизвестных;
6)построить окончательные эпюры внутренних силовых факторов M, N,Q.
Числовые данные: l 4 м, h = 2 м, q = 10 кН/м, К = 2.
Решение.
Расчет производится методом сил.

107
|
|
kJ |
|
|
J |
|
J |
J |
q |
0,5l |
l |
|
l |
|
|
|
|||
A |
B |
|
C |
|
Рис. 6.8
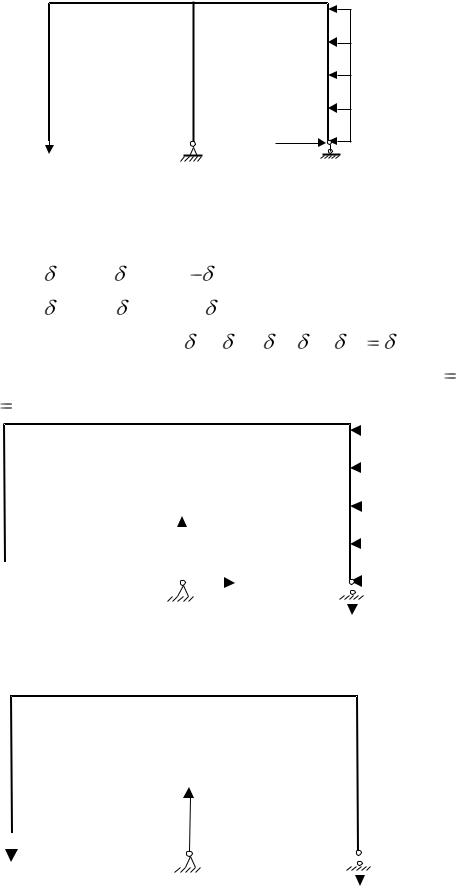
1.Заданная система (см. рис. 6.8) два раза статически неопределима, так как для определения пяти реакций связей имеем три уравнения равновесия (система сил, произвольно расположенных на плоскости).
2.Выбираем основную систему для решения (рис. 6.9,а) и для проверки
(рис. 6.9,б).
3.Эквивалентная система, соответствующая основной (см. рис. 6.9,а), изображена на рис 6.10.
a) |
б) |
|
Рис. 6.9
108
Э.С. |
q |
x2 |
x1 |
|
Рис.6.10 4. Записываем канонические уравнения метода сил для два раза стати-
чески неопределимой системы
11X1  12 X 2
12 X 2  1p ;
1p ;
21X1  22 X 2
22 X 2  2 p .
2 p .
5. Определяем перемещения 1p , 2 p , 11, 22, 12 |
|
|
21способом Ве- |
|||||||||||||
рещагина. Для этого рассмотрим состояния " P" (рис. 6.11), " X1 1" (рис. |
||||||||||||||||
6.12) и " X2 1" (рис. 6.13). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RP |
|
|
|
“P” |
|
|
|
|
|
|
q |
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
B |
|
|
|
H P |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
B |
|
|
|
|
|
B |
C |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R P |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
Рис. 6.11 |
|
|
|
|
|
|
|
|||||||
|
|
R(2) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
B |
|
|
|
“x2=1” |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
B |
|
|
|
|
|
|
C |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R(2) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
Рис. 6.12
109
|
|
“x1=1” |
|
|
R(1) |
|
|
|
B |
|
|
|
B |
1 |
C |
H (1) |
|
||
|
|
R(1) |
|
B |
|
|
|
|
|
|
C |
Рис. 6.13
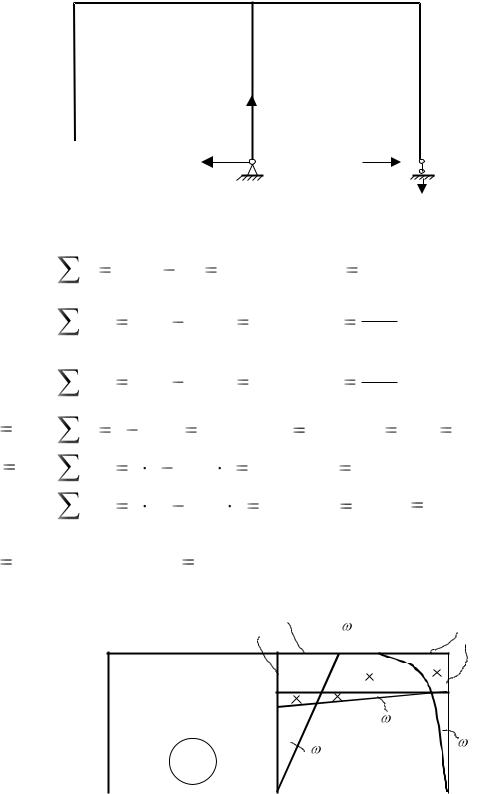
Определяем реакции опор B и C для каждого из этих состояний:
" P" x Hb( p) qh 0 ;
|
|
mB |
|
qh2 |
|
RC( p)l |
0; |
||
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
||
|
|
m |
|
|
qh2 |
R( p)l |
0; |
||
|
|
A |
|
|
|
||||
|
|
|
2 |
|
B |
|
|
||
|
|
|
|
|
|
|
|
||
" X1 |
1" |
x 1 |
|
H B(1) |
0; |
|
HB(1) |
||
" X2 |
1" |
mB |
1 l RC(2) |
l |
0; |
||||
|
|
m |
|
1 2l |
R(2) |
l |
0 ; |
||
|
|
C |
|
|
|
B |
|
|
|
Hb( p)
RC( p)
RB( p)
1;
RC(2)
RB(2)
qh ; qh2
2l
;
qh2
2l
;
RC(1) RB(1) 0;
1;
2; HB 0.
Строим эпюры изгибающих моментов для состояний " P" (рис. 6.14),
" X1 1" (рис. 6.15) и " X2 1" (рис. 6.16). Тогда
ql 2 |
|
ql 2 |
4 |
P |
8 |
|
||
|
|
P |
|
P |
P |
M XP |
|
|
|
|
Рис.6.14
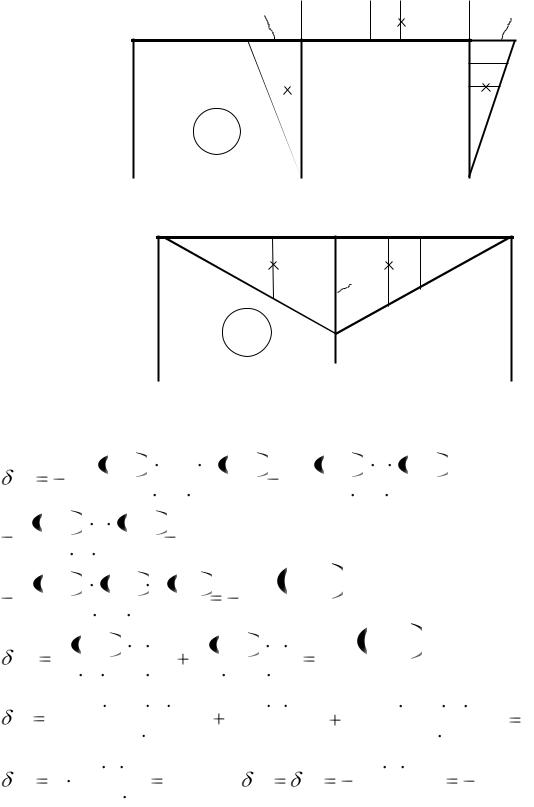
110
0.5l 
 0.5l
0.5l
M X 1
Рис. 6.15 |
l |
M X 2 |
Рис. 6.16
|
|
|
|
|
|
1 q 0,5l 2 |
|
0,5l |
|
3 0,5l |
|
1 q 0,5l 2 l |
|
0,5l |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 EI |
4 |
|
|
|
|
|
2 |
|
|
|
|
2 EI |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
q 0,5l |
|
2 l |
0,5l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 2 EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
q 0,5l |
2 |
|
|
0,5l |
2 05l |
|
|
|
580 кНм3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 EI |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3EI |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
q 0,5l 2 |
l |
2l |
q 0,5l 2 |
l |
l |
|
400 кНм3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
2 2 2EI 3 |
|
|
2 2EI 2 |
|
|
|
|
|
|
3EI |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
1 0,5l |
0,5l |
2 0,5l |
|
|
0,5l |
l |
0,5l 1 0,5l |
0,5l |
2 |
0,5l 40м3 |
; |
||||||||||||||||||||||||||||||||||||
11 |
2 |
|
|
|
|
|
|
|
|
EI 3 |
|
|
|
|
|
2EI |
|
|
|
2 |
|
|
|
|
|
EI |
3 |
|
|
|
|
3EI |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
1 l |
l |
2l |
|
|
64м3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 l |
l |
0,5l |
|
|
8м3 |
|
|
|
||||||||||||||||||
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
12 |
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||
|
|
2 EI |
3 |
|
|
|
|
3EI |
|
|
|
|
|
2 |
|
|
2EI |
|
|
EI |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
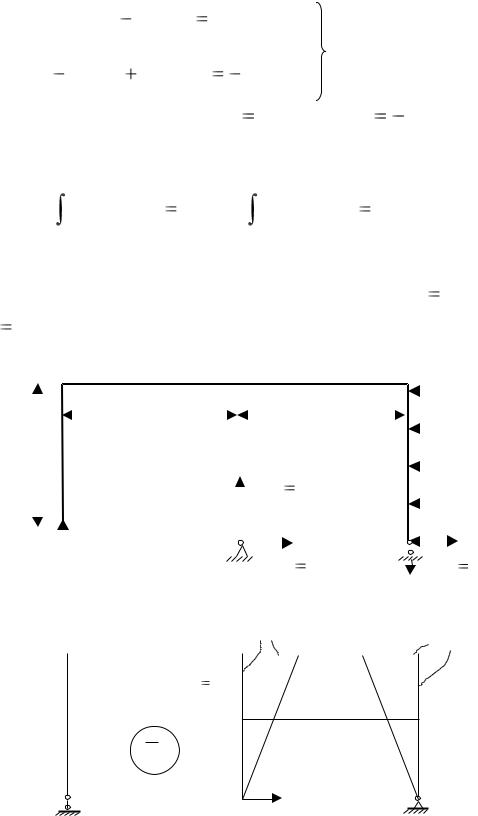
6. Решаем систему канонических уравнений
|
|
|
|
|
|
|
|
|
|
|
111 |
|
|
40 |
|
X1 |
8 |
X 2 |
580 |
, |
|
||||
|
3EI |
|
|
3EI |
||||||||
|
|
EI |
|
|
||||||||
8 |
|
X1 |
|
64 |
X 2 |
|
400 |
. |
||||
|
|
EI |
|
|
||||||||
|
|
|
|
3EI |
|
3EI |
||||||
В результате решения получим X1 |
13,78кН; X 2 1,05кН . |
|||||||||||
Для проверки решения воспользуемся другой основной системой (см. рис. 6.9,б). Проверим справедливость равенств
|
|
|
|
|
|
|
|
|||
|
M xэM x1 |
dz 0; |
|
M xэM x2 |
dz 0 , |
|||||
l |
EI |
l |
EI |
|||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|||
где M xэ - изгибающий момент для эквивалентной системы (рис. 6.17),
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M x1, M x2 - изгибающие моменты для состояний |
" X1 1" |
(рис. 6.18) и |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
" X 2 1" (рис. 6.19) соответственно. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
D |
|
|
E |
|
|
|
F |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4м |
|
|
|
|
|
|
|
|
4м |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10кн/м |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
RB |
2,9кн |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
C |
|
|
|
|
|
|
|
13.78кн |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1.05кн |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
HB |
6,13кн |
|
|
|
|
|
RC |
3,95кн |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.17 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.5l |
|
|
|
|
|
|
0.5l |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
" X1 |
1" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M X 1
1
Рис. 6.18
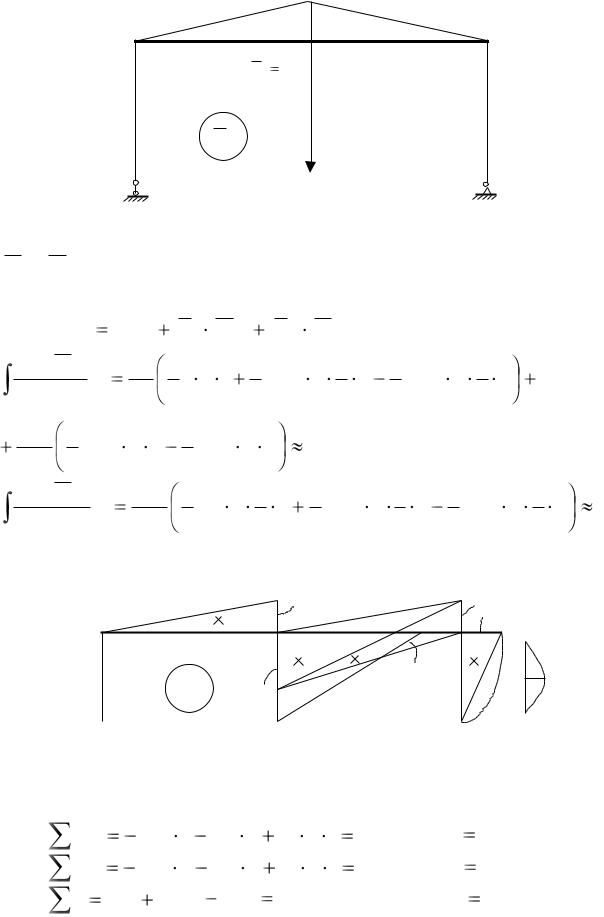
|
|
|
112 |
|
|
|
|
|
|
l |
|
|
|
|
|
" X 2 |
1" |
|
|
|
|
M X 2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Рис. 6.19 |
|
|
|
Воспользуемся |
способом |
Верещагина. |
Эпюры |
изгибающих |
моментов |
|
M x1, M x2 , M xэ представлены на рис. 6.18, 6.19, 6.20 соответственно. Эпюра |
|||||||||||||||||||||||||||||||
M xэ |
построена по принципу независимости действия сил с помощью урав- |
||||||||||||||||||||||||||||||
нения M xэ |
M xp |
|
X1 |
M x1 |
|
X 2 |
M x2 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
M xэM x1 |
dz |
1 2 |
5 |
|
2 1 |
|
1 |
7,74 |
2 |
2 |
2 |
|
1 |
2,26 |
2 |
2 |
2 |
|
|
|
|
|||||||||
|
EI |
|
|
EI |
|
3 |
|
|
2 |
3 |
|
2 |
3 |
|
|
|
|
||||||||||||||
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
7,74 |
4 |
2 |
|
1 |
8,06 |
4 |
2 |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2EI |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M xэM x2 |
dz |
1 1 |
4,2 |
4 |
2 |
2 |
1 |
7,74 |
4 |
1 |
2 |
1 |
8,06 |
4 |
2 |
2 |
|
0 . |
||||||||||||
|
|
EI |
|
|
|
2EI |
|
2 |
3 |
2 |
3 |
2 |
3 |
|
|||||||||||||||||
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значит X1 |
|
и X2 определены верно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4,2 |
|
|
|
|
|
|
|
|
7,74 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q(2)2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
MXЭ |
8,06 |
|
|
|
|
|
|
|
12,26 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
КНМ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
8. Для эквивалентной системы с найденными значениями |
X1 |
и |
X2 |
||||||||||||||||||||||||||
(см. рис. 6.17) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
а) определяем реакции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
mC |
1,05 8 |
|
RB |
4 |
|
10 2 1 |
0; |
|
RB |
|
2,9кН ; |
|
|
|
||||||||||||||
|
|
|
mB |
1,05 4 |
|
RC |
4 |
|
10 2 1 |
0 ; |
|
RC |
|
3,95кН ; |
|
|
|
||||||||||||||
|
|
|
x |
|
H B |
13,87 |
10,2 |
|
0; |
|
|
|
|
|
|
HB |
|
6,13кН ; |
|
|
|
||||||||||
|
|
б) записываем выражения для N , |
Q , |
M по участкам. |
|
|
|
|
|
||||||||||||||||||||||

|
|
|
|
|
|
113 |
|
|
|
|
Участок AD: 0 |
z |
2; |
N |
1,05кН;Q 0; M |
0 . |
|
|
|
||
Участок DЕ: 0 |
z |
4; N |
0;Q 1,05кН; M 1,05z; M D |
0; M E |
4,2кНм. |
|||||
Участок ВЕ: 0 |
z |
2; |
N |
2,9кН;Q 6,13кН; M 6,13z; |
|
|||||
M B |
0; M E |
12,26кНм. |
|
|
|
|
|
|||
Участок ЕG: 0 |
z |
4; |
N |
6,13кН ;Q 1,05 |
2,9 3,95кН ; |
|
||||
M |
1,05 4 |
z |
2,9z |
6,13z; M E |
8,06кНм; MG |
7,74кНм. |
|
|||
Участок |
|
|
|
|
|
|
|
CG: 0 z |
2; |
|
|
N 3,85кН ;Q |
13,87 10z ; QC 13,87кН ; |
|
|
|
|||||
QG |
6,13кН . Так как Q меняет знак, то определяем z |
из уравнения |
|
|||||||
dM |
dz Q |
13,87 10z |
0; z 1,39м ; M |
13,87z |
10z2 / 2; |
|
||||
MC |
0 ; M z |
|
9,12кНм ; MG |
7,74кНм. |
|
|
|
|
||
Строим эпюры N (рис. 6.21), Q (рис. 6.22), M (рис. 6.23).
N (кн) |
|
|
|
1,05 |
2,9 |
6,13 |
3,95 |
|
Рис. 6.21
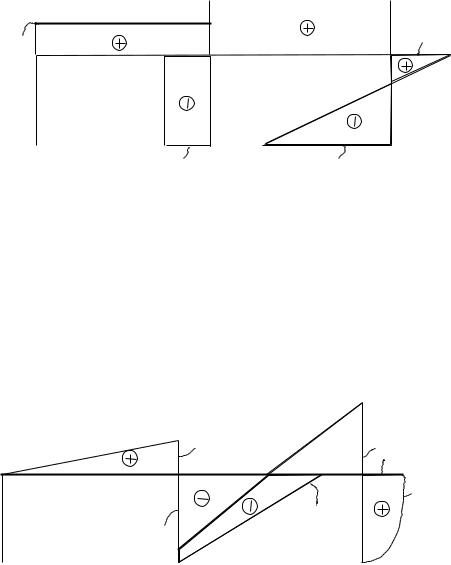
114
3,95
6,13
1,05
Qy (кн)
6,13 |
13,78 |
Рис. 6.22
|
|
|
4,2 |
7,74 |
|
|
|
|
|
|
|
|
|
9,12 |
M X |
(КНМ ) |
8,06 |
|
12,26 |
|
|
|||
|
|
|
|
Рис. 6.23
6.4. ИЗГИБ КРИВОГО БРУСА
115
До сих пор рассматривались задачи, связанные с расчетом прямых брусьев. Рассмотрим теперь расчет кривых брусьев, т.е. брусьев, имеющих криволинейную ось. К расчетной схеме кривого бруса сводится расчет крюков, проушин, звеньев цепей, арок мостов, сводов и т.д.
Наибольшее практическое значение имеют плоские кривые брусья, оси которых – плоские кривые, а нагрузки расположены в плоскости кривизны бруса.
6.4.1. Определение внутренних силовых факторов
Внутренние усилия в поперечных сечениях кривого бруса определяются так же, как в балках и рамах, методом сечения. В общем случае в поперечных сечениях плоского кривого бруса возникают три внутренних силовых фактора: изгибающий момент М х , поперечная сила Qy и нормальная сила
N .
Изгибающий момент считается положительным, если ему соответствует увеличение кривизны оси бруса. Правила знаков для нормальной и поперечной сил остаются такими же, как и для прямого бруса.
При построении эпюр значение М х , Qy , N откладывают по нормали
геометрической оси кривого бруса, т.е. по радиусу кривизны. При этом положительные значения откладывают в сторону от центра кривизны, а отрицательные значения – к центру кривизны.
6.4.2. Расчет на прочность кривых брусьев
Принято различать брус малой и большой кривизны. Основным признаком такого деления является отношение высоты сечения h в плоскости кривизны к радиусу кривизны оси бруса o . Если это отношение существен-
но меньше единицы ( h / o 0,2 ), считается, что брус имеет малую кривиз-
ну. Для бруса большой кривизны отношение h / o соизмеримо с единицей.
Расчетные формулы, полученные ранее для прямого бруса, применимы также и к брусу малой кривизны. Исключением является формула, связывающая кривизну нагруженного бруса с изгибающим моментом. В случае бруса малой кривизны она записывается в виде
1 1 |
|
M x |
, |
||
|
|
o |
|
EI x |
|
|
|
|
|
||
