
Учебное пособие 800486
.pdf
86
ных точках участков (число которых n – 1) должны быть равны прогибы и углы поворота.
Если балка состоит из участков постоянной жесткости EI x , дифференциальное уравнение упругой линии можно записать в виде
EI x yk M xk , |
k 1,...,n . |
(6.12) |
Число постоянных интегрирования |
уравнения (6.12) сводится к двум, |
|
если при составлении выражений для M xk |
и интегрировании (5.12) исполь- |
|
зуются следующие приемы.
1. Начало координат выбирают в крайнем сечении балки и абсциссу произвольного сечения на каждом участке отсчитывают от начального сече-
ния, так что для k-го участка можно записать аk |
1 |
z ak , где аk |
1, ak - |
||||||
абсциссы начала и конца k-го участка, для первого участка a0 |
= 0, для по- |
||||||||
следнего ak |
l , где l |
длина балки. |
|
|
|
|
|||
|
|
2. Если а j |
абсцисса приложения сосредоточенного момента M j , |
||||||
то |
в |
выражении |
для |
изгибающего момента |
его |
учитывают |
в виде |
||
M j |
z |
a j |
0 . |
|
|
|
|
|
|
|
|
3. Если равномерно распределенная нагрузка заканчивается в сечении |
|||||||
z |
ak |
l , |
то ее продолжают до конца балки, и от сечения z |
ak |
прикла- |
||||
дывают нагрузку противоположного направления.
4. Интегрирование уравнения (6.12) ведется без раскрытия скобок. Выполнение п.п. 1 – 4 приводит к автоматическому выполнению усло-
вий равенства прогибов и углов поворота в смежных точках участков и равенствам
C1 |
C2 Cn |
EI x 0 ; D1 D2 Dn EI x y0 , (6.13) |
где 0 , y0 |
угол поворота и прогиб начального сечения, которые называют |
|
начальными параметрами.
Полученные после интегрирования уравнения прогибов и углов пово-
рота для k го участка при аk |
1 |
z ak |
|
|
|
|
|
|
|
|
|
2 |
|
q j |
z a j |
3 |
|
k 1 |
|
|
Pj z a j |
|
|
|
||
EI x yk EI x k EI x 0 |
M j |
z a j |
|
|
|
|
|
; |
2 |
|
|
6 |
|
||||
j 0 |
|
|
|
|
|
|
(6.14)

|
|
87 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
Pj z a j |
3 |
|
q j |
z a j |
4 |
|
|
|
k 1 |
|
M j z a j |
|
|
|
|
|
||||
EI x yk |
EI x y0 EI x 0 z |
|
|
|
|
|
|
|
|
|
|
, |
2 |
|
6 |
|
|
|
24 |
|
|||||
|
j 0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
(6.15) |
||
где а j |
абсцисса начала j – го участка, M j , Pj |
- сосредоточенный момент и |
||||||||||
сила, приложенные в начале j – го участка, q j |
- интенсивность равномерно |
|||||||||||
распределенной нагрузки, абсцисса начала которой а j . |
При этом положи- |
|||||||||||
тельными считают M j , Pj , q j , |
изгибающие балку выпуклостью вниз. Нача- |
|||||||||||
ло координат можно брать на любом из крайних сечений балки, если начальное сечение левое, то 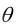 0 означает, что сечение поворачивается против часовой стрелки, если правое – по часовой.
0 означает, что сечение поворачивается против часовой стрелки, если правое – по часовой.
Среди сосредоточенных нагрузок могут быть реакции связей. Если балка статически определима, то реакции определяют из уравнений равновесия. Начальные параметры определяют из условий закрепления.
6.1.2.3. Определение перемещений методом Мора Метод Мора представляет собой универсальный метод определения
линейных и угловых перемещений в любых плоских и пространственных системах.
Для того чтобы определить методом Мора перемещение i (прогиб или угол поворота) в некотором сечении балки или рамы необходимо:
1)кроме «грузового» состояния («Р»), представляющего собой балку (или раму), нагруженную заданными нагрузками, рассмотреть «единичное» состояние, то есть ту же самую балку (или раму), освобожденную от заданных нагрузок и нагруженную единичным силовым фактором (единичной силой, когда определяется прогиб, или единичным моментом, когда определяется угол поворота), приложенным в сечении, перемещение которого определяется, и ориентированным в направлении искомого перемещения;
2)оба эти состояния разбить на одинаковые участки;
3)на каждом k – м участке записать аналитическое выражение изги-
бающих моментов, соответствующих «грузовому» состоянию M xpk |
и |
|
«единичному» состоянию M xik |
; |
|
4) определить искомое перемещение, как сумму интегралов Мора по участкам балки (или рамы)

|
88 |
|
|
|
|
|
k |
|
k |
|
|
n |
M xp M xi |
|
|
||
|
|
|
|
|
|
i |
|
|
|
dz, |
(6.16) |
EIx |
|
|
|||
|
|
|
|
||
k 1 |
k |
|
|
|
|
lk |
|
|
|
|
|
где n – число участков; k – номер участка; |
lk длина участка; |
EI x k из- |
|||
гибная жесткость k – го участка.
Если |
i |
0, то направление искомого перемещения совпадает с на- |
||
|
|
|
|
|
правлением единичного силового фактора, если |
i |
0, то противоположно |
||
|
|
|
|
|
ему.
6.1.2.4. Определение перемещений при изгибе способом Верещагина Если брус состоит из прямолинейных участков с постоянной в преде-
лах каждого из них жесткостью, то интегралы Мора можно вычислять по способу Верещагина.
Определение способом Верещагина перемещений i (прогиба или уг-
ла поворота) некоторого сечения балки (или рамы) ведут в следующей последовательности:
1) строят независимо друг от друга эпюру изгибающих моментов
( M xp ) для «грузового» состояния и эпюру изгибающих моментов ( M xi ) для «единичного» состояния, соответствующего искомому перемещению;
2)обе эти эпюры разбивают на одинаковые участки, в пределах каждого из которых эпюра изгибающих моментов «единичного» состояния изменяется по монотонному линейному закону, а изгибная жесткость сечения балки (или рамы) постоянна;
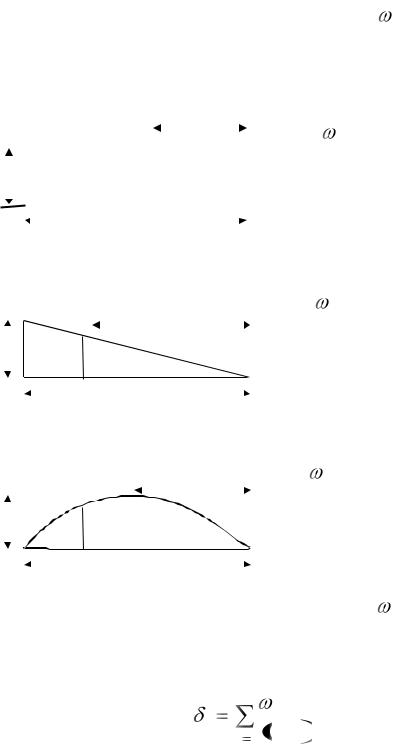
3)эпюру изгибающих моментов «грузового» состояния разбивают на простейшие фигуры (прямоугольники, треугольники и т.п.), для каждой из
которых определяют площадь |
k |
положение ее центра тяжести. Значения |
|
|
площадей и положения их центров тяжести для некоторых простейших фигур приведены в табл.6.1.
89
Таблица 6.1
|
|
|
|
|
|
|
|
|
Эпюра M xp |
|
Площадь k |
|
Координата центра |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тяжести z ck |
||||
|
|
|
|
|
|
|
|
|
|
прямоугольник |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zKc |
|
|
|
|
|
|
|
|
|
c |
|
b |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = bh |
|
|
z k = |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
прямоугольный треугольник |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zKc |
|
|
|
|
|
|
|
k |
= |
|
bh |
|
|
z ck = |
2 |
b |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|||||||||||||||||||
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
параболический сегмент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zKc |
|
|
|
|
|
k |
= |
2 |
bh |
|
z ck = |
b |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
4) под центром тяжести каждой площади |
k |
определяют ординату |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M ki на эпюре изгибающих моментов «единичного» состояния; |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
5) искомое перемещение определяется как алгебраическая сумма |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
k M ki |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
(6.17) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EIx k |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
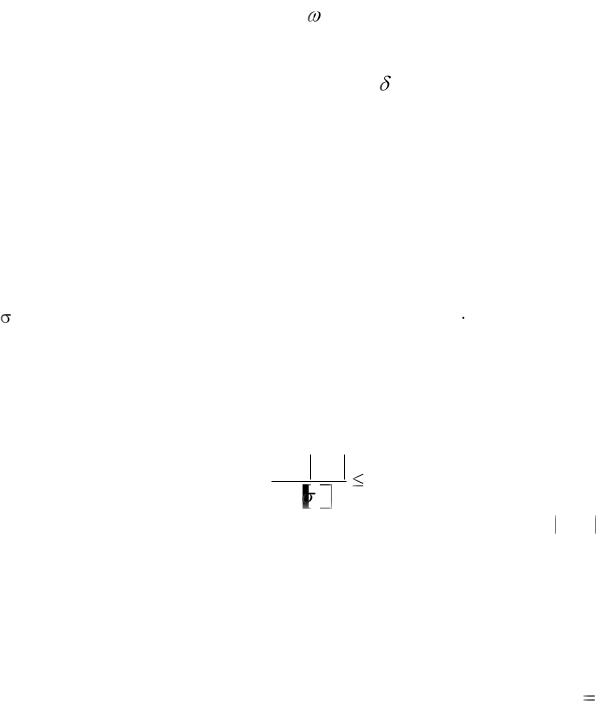
где k – номер площади; m – число простейших фигур, на которые разбита эпюра изгибающих моментов «грузового» состояния. Произведение  считается положительным, если часть эпюры изгибающих моментов «грузо-
считается положительным, если часть эпюры изгибающих моментов «грузо-
90
вого» состояния, имеющая площадь k , и соответствующая ей ордината
M ki расположены по одну сторону от нулевой линии.
Положительное значение перемещения |
i |
получается в случае, если |
|
|
его направление совпадает с направлением единичного силового фактора (единичной силы или момента).
6.2. Расчет статически определимых балок
Задача 1. Для заданной схемы балки (рис 6.4) написать выражения Qy
и M x для каждого участка в общем виде, построить эпюры Qy и M x , найти
M x max и подобрать стальную балку двутаврового поперечного сечения при
[ ] = 1600 кг/см 2 = 160 МПа; q = 1 т/м = 1 10 4 Н/м; Р = 2 10 4 Н; а = 2 м; b = 4 м.
10 4 Н/м; Р = 2 10 4 Н; а = 2 м; b = 4 м.
Решение.
Под действием приложенных нагрузок балка работает на изгиб. По условию задачи требуется провести проектный расчет. Из условия прочности по нормальным напряжениям (6.4)расчет ведется по соотношению
max M x |
Wx . |
|
Для определения расчетного изгибающего момента max М х (в
опасном сечении) необходимо построить эпюры поперечной силы Qy и из-
гибающего момента М х .
1. Определение реакций опор.
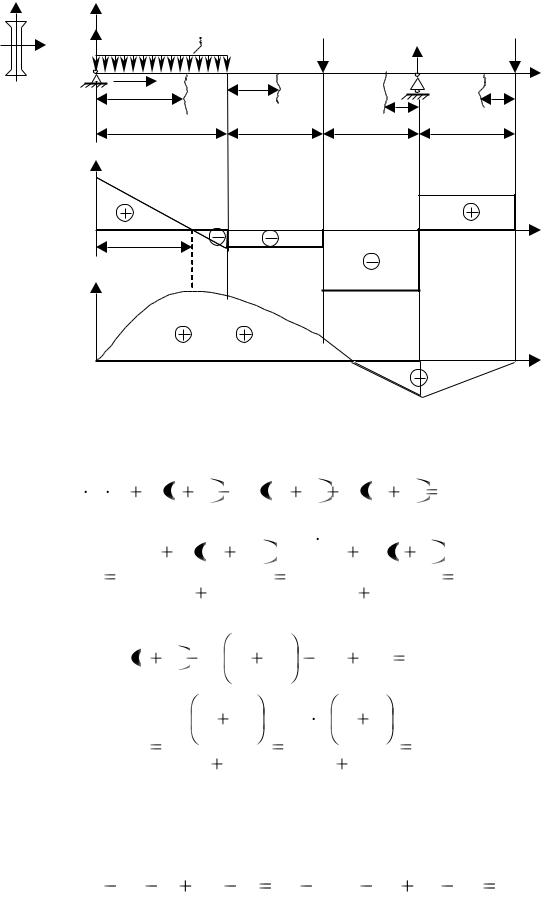
Определив типы опор и мысленно заменив их соответствующими реакциями (см. рис. 6.4,а), установим их величины.
Так как горизонтальные и наклонные силы отсутствуют, то Rz 0 . Для определения реакций RA и RB записываем два уравнения равновесия.
|
|
|
|
|
91 |
|
|
|
|
|
y x |
y |
|
|
|
|
|
|
|
|
|
|
RA |
I |
q |
II |
P |
IV |
RB |
III |
P |
|
|
A |
|
|
|
z2 |
|
|
B |
E |
Z a) |
|
|
|
R |
C |
D |
|
z4 |
z3 |
||
|
|
|
z |
|
|
|
|
|
||
|
|
|
z1 |
|
|
|
|
|
|
|
Qy |
, кН |
|
b |
|
a |
|
a |
|
a |
|
30 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
б) |
|
|
|
* |
10 |
|
10 |
|
|
|
Z |
M X , кНм |
z1 |
|
|
|
|
|
|
|
||
|
45 |
|
40 |
30 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
Z в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
Рис. 6.4 |
|
|
|
|
|
Уравнение моментов всех сил относительно точки А |
|
|||||||||
q b |
b |
|
P a |
b |
|
R |
2a |
|
b |
|
P 3a |
b 0 , отсюда |
||||||||||||||
|
|
|
||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
qb |
2 |
|
P 4a |
|
2b |
|
|
|
|
10 16 |
|
|
20 8 |
8 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Rb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50кН . |
|||
|
|
|
2a |
|
b |
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Уравнение моментов всех сил относительно точки В |
||||||||||||||||||||||||||
RА a |
|
b |
|
qb |
|
b |
|
|
2a |
|
Pa |
Pa |
0, отсюда |
|||||||||||||
|
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
qb |
|
b |
|
2a |
10 4 |
4 |
|
4 |
|
|
|
||||||||
|
RA |
|
2 |
|
2 |
|
30кН . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
a |
b |
|
|
|
|
2 |
4 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Обе реакции получились положительными. Это означает, что их действительное направление совпадает с выбранным. Для проверки правильности определения реакций опор спроектируем все внешние силы, приложенные к балке, на вертикальную ось Y
RA qb P RB P 30 10  4 20 50 20 0.
4 20 50 20 0.

92
Уравнение удовлетворяется тождественно, значит реакции опор определены верно.
2. Построение эпюр поперечных сил и изгибающих моментов. Разбиваем балку на 4 участка. Границами участков являются точки A,
B, C, D, E. Положение произвольного поперечного сечения на участках характеризуется соответствующими координатами z1, z2 , z3 , z4 . Записываем
выражение для поперечных сил и изгибающих моментов по участкам, используя выражения (6.1), (6,2) и правила знаков (см. рис. 6.2).
Участок 1: 0 z1 b. Рассматриваем часть балки, расположенную по
левую сторону от сечения с координатой z1 |
|
|
|
|
|
|
||||
Q 1 |
R |
A |
qz ; |
M 1 |
R |
A |
z |
qz12 |
. |
|
|
|
|||||||||
y |
|
1 |
x |
|
1 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Координата z входит в выражение для Q 1 |
в первой степени (Q 1 |
- |
||||||||
1 |
|
|
|
|
|
y |
|
|
y |
|
линейная функция z1). Для построения эпюры Qy1 достаточно определить
достаточно определить
значения ее ординат на границах участков: z1 = 0, Qy1 = RA = 30 кН;
= RA = 30 кН;
z |
= b, |
Q 1 |
= R |
A |
qb= 30 |
10 4 = 10 кН; |
|
1 |
|
y |
|
|
|
|
|
Изгибающий момент M 1 |
является квадратичной функцией z |
. Для |
|||||
|
|
|
|
|
x |
1 |
|
построения квадратичной параболы необходимо определить как минимум три значения изгибающего момента, два из которых определяем на границах участков:
z |
= 0, M 1 |
= 0; |
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
= b, M 1 |
|
|
|
qb2 |
10 16 |
|
||
z |
= R |
A |
b |
|
30 4 |
|
|
40 кНм. |
|
|
|
|
|||||||
1 |
x |
|
|
2 |
|
2 |
|
||
|
|
|
|
|
|
|
|||
Так как поперечная сила Qy1 меняя знак в одном из сечений (обозна-
меняя знак в одном из сечений (обозна-
чим его через z1 ) обращается в нуль, то в соответствии с дифференциальными зависимостями (6.3) изгибающий момент в этом сечении будет иметь экс-
тремум. Приравнивая выражение Qy1 нулю, определяем координату сечения
нулю, определяем координату сечения
z1
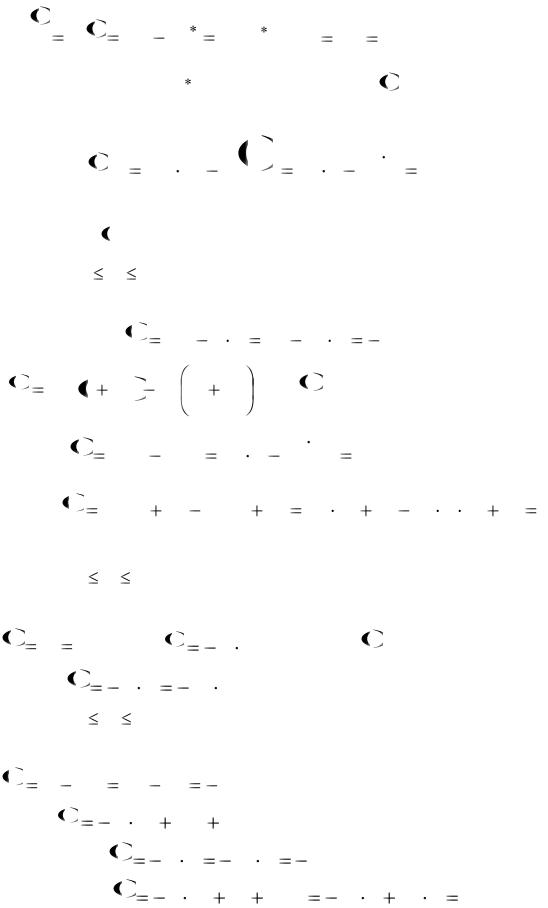
93
|
dM x1 |
1 |
|
|
|
|
|
RA |
30 |
|
|
|
|
|
|||
|
|
Qy |
RA |
qz1 |
0 ; z1 = |
|
|
|
|
|
|
3 м. |
|
||||
|
dz |
q |
10 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Подставляя значение |
z |
= 3 м выражение |
M |
1 |
, определим экстре- |
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
мальное (максимальное) значение изгибающего момента на этом участке |
|||||||||||||||||
|
|
1 |
|
* |
|
q z1* 2 |
|
|
|
10 9 |
|
|
|||||
|
|
M x max |
RA z1 |
|
|
|
30 3 |
|
|
|
|
|
|
45 кНм. |
|||
|
|
2 |
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Найденное значение изгибающего момента будет третьим значением ординаты эпюры M x1 для построения параболы.
для построения параболы.
Участок 2: 0 z2 а. Рассматриваем равновесие части балки, расположенной слева от сечения с координатой z2
|
|
|
|
|
|
|
Qy2 |
|
RA |
q b 30 10 4 10 кН; |
|
||||||||||
M x2 |
RA |
b |
z2 |
qb |
b |
|
z2 |
; ( M x2 |
- линейная функция z2 ). |
||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
z |
|
= 0, |
M |
|
2 |
R b |
|
qb2 |
30 4 |
10 16 |
40 кНм; |
|
|||||||||
2 |
x |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
A |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z2 = а, M x2 |
RA (b a) qb( |
b |
|
|
a) 30 (4 2) 10 4 (2 2) 20 |
||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
кНм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Участок 3: |
0 |
z3 а. Рассматриваем равновесие части балки, |
располо- |
||||||||||||||||||
женной справа от сечения с координатой z3 |
|
|
|
||||||||||||||||||
Qy3 |
P 20 кН; M x3 |
P z3 ; z3 = 0, M x3 = 0; |
|
||||||||||||||||||
z3 = а, M x3 |
P a |
|
20 2= - 40 кНм. |
|
|
|
|||||||||||||||
Участок 4: |
0 |
z4 а. Рассматриваем равновесие части балки, |
располо- |
||||||||||||||||||
женной справа от сечения с координатой z4 |
|
|
|
||||||||||||||||||
Qy4 |
P |
|
RB |
20 |
50 |
|
|
|
30 кН; |
|
|
|
|||||||||
|
|
M x4 |
|
P (a z4 ) |
RB z4 ; |
|
|
|
|||||||||||||
|
|
z4 =0, M x4 |
P a |
20 2 40 кНм; |
|
||||||||||||||||
|
|
z |
4 |
= а, M 4 |
|
P (a |
а) |
|
R а |
|
20 4 50 2 20 кНм. |
||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
B |
|
|
|
||

94
Строим эпюру Qy (см. рис. 6.4,б), располагая ее строго под схемой
балки. Положительные значения Qy откладываем выше нулевой линии (ко-
торая проводится параллельно оси балки), а отрицательные - ниже.
Строим эпюру изгибающих моментов, располагая ее строго под эпюрой Qy (см. рис. 6.3,в). Положительные значения M x откладываем выше
нулевой линии, отрицательные – ниже. Используя дифференциальные зависимости (6.3) и правила, вытекающие непосредственно из метода сечений,
проводим проверку правильности построения эпюр Qy и M x . Устанавливаем изгибающий момент в опасном сечении max M x 45 кНм.
3. Подбор размеров поперечного сечения балки. |
|
|||||||||
Подбор сечения балки ведем из условия прочности (6.4) |
|
|||||||||
|
|
|
|
45 106 |
|
|
|
|||
Wx |
max |
M |
x |
|
281,25 103 мм3 |
281,25 |
см 3 . |
|||
|
|
|
|
|
|
|||||
|
|
|
160 |
|||||||
|
|
|
|
|
|
|
||||
Используя таблицу сортамента прокатной стали для двутавров 1 , по значению осевого момента сопротивления Wx выбираем двутавр № 24, у ко-
торого W (24) |
289 см 2 . |
х |
|
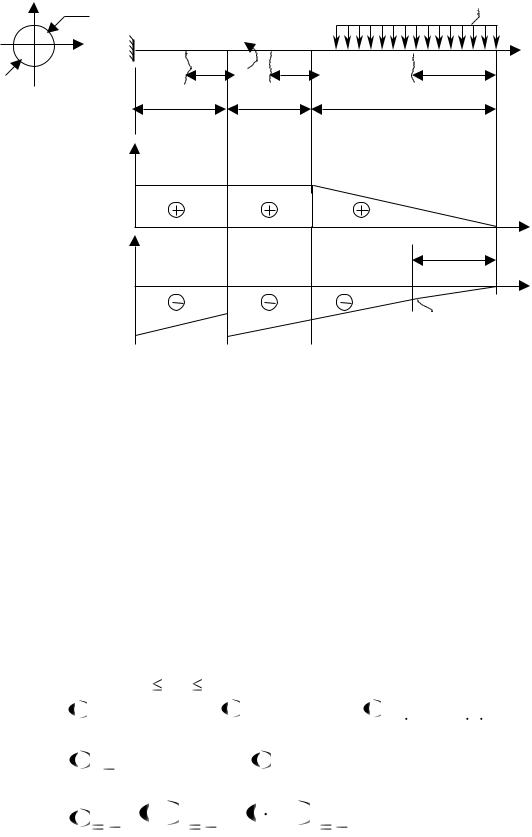
Задача 2. Для заданной расчетной схемы (рис. 6.5,а) подобрать из условия прочности деревянную балку круглого поперечного сечения при  = 80 кг/см 2 = 8 МПа; а = 0,5 м; q = 2 т/м = 20 кн/м; М = 1 тм = 10 кНм.
= 80 кг/см 2 = 8 МПа; а = 0,5 м; q = 2 т/м = 20 кн/м; М = 1 тм = 10 кНм.
Решение Под действием нагрузок, приложенных к балке, она работает на изгиб.
По условию задачи требуется провести проектный расчет. Из условия прочности по нормальным напряжениям (6.4) расчет ведем по соотношению
|
|
|
Wx |
max |
M x |
. |
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Учитывая, что для круглого сечения W |
|
|
|
d 3 32, получим |
|||||||
|
|
|
|
|
|
|
x |
|
|
|
|
d |
3 |
|
32 max |
|
M x |
|
. |
|
|||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
Для определения расчетного изгибающего момента max M x необходимо построить эпюры поперечной силы Qy и изгибающего момента M x .
|
|
|
|
|
|
|
95 |
|
|
|
|
y |
d |
|
|
|
|
|
|
I |
q |
|
|
|
|
|
III |
|
MII |
|
|
||||
|
|
|
|
|
|
|
A |
|
|||
|
|
|
x |
D |
C |
B |
|
|
|||
|
|
|
|
|
|
|
a) |
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Z3 |
|
Z2 |
|
Z1 |
Z |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a |
|
2a |
|
|
|
|
Qy , кН |
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
б) |
|
M |
X |
, кНм |
|
|
|
|
|
Z1=a |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
10 |
2,5 |
Z |
в) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
20 |
|
20 |
|
|
|
|
|
Рис. 6.5 1. Определение реакции опор.
Так как балка имеет опору только с одной стороны, то нет необходимости определять реакции в опоре, в связи с тем, что эпюры Qy и M x можно
построить, проводя рассмотрение от свободного конца балки.
2. Построение эпюр поперечных сил и изгибающих моментов. Разбиваем балку на три участка (см. рис. 6.5,а). Границами участков
являются сечения A, B, C, D. Положение произвольного поперечного сечения на участках характеризуется координатами z1, z2 , z3. Применяя метод се-
чений и рассматривая равновесие части балки не содержащей защемление, записываем выражения для поперечных сил и изгибающих моментов по участкам.
Участок 1: 0 |
z1 |
2а. |
|
|
|
|
|
||||||||||
Q |
1 |
= q z |
; z = 0, |
Q |
y |
1 = 0; z = 2а, Q |
1 |
= q 2a = 20 2 0,5 = 20 кН; |
|||||||||
|
у |
|
1 |
1 |
|
|
|
|
1 |
|
|
y |
|
||||
|
1 |
|
|
qz2 |
|
|
= 0, M 1 |
|
|
|
|
|
|||||
M |
= |
|
|
|
1 |
; |
z |
= 0; |
z = 2а, |
|
|||||||
х |
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
1 |
|
|
х |
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M х1 |
|
|
|
q 2a 2 |
|
|
20 2 0,5 |
2 |
10 кНм. |
||||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
