
Учебное пособие 800486
.pdf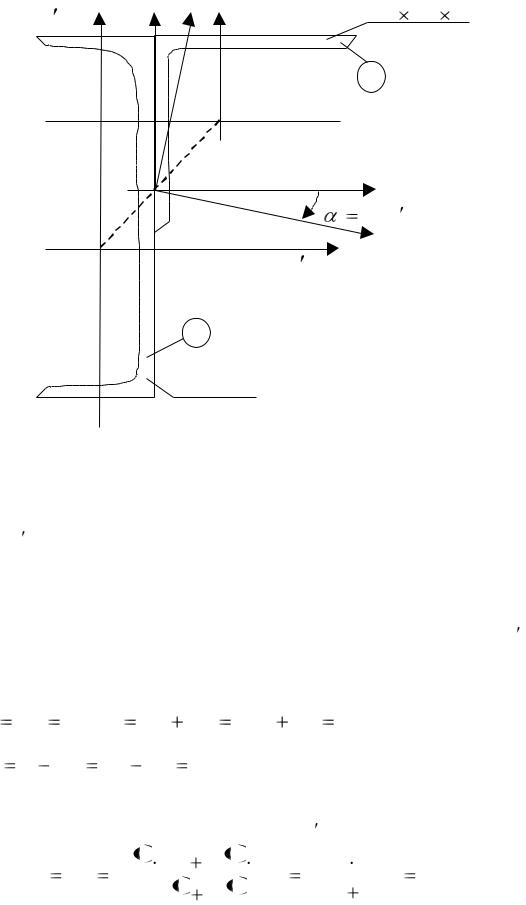
|
|
76 |
|
|
|
yC |
y |
yC2 |
|
|
160 160 10 |
y , yc1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
c2 |
|
|
xC2 |
|
|
|
|
|
|
|
c |
|
|
|
xC |
|
|
|
x |
0 |
1345 |
|
|
|
|
||
с,c |
|
|
x , xc1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
N 30 |
|
|
|
|
Рис. 5.3 Решение.
1.Вычерчиваем сечение в масштабе. Проводим вспомогательные оси координат X ,Y через центр тяжести швеллера.
через центр тяжести швеллера.
2.Разбиваем составное сечение на две простые фигуры – швеллер (элемент № 1) и равнобокий уголок (элемент № 2). Для каждой простой фигуры определяем с помощью таблиц сортамента прокатной стали [1] пло-
щадь, координаты центра тяжести относительно вспомогательных осей X ,Y и заносим в табл. 5.1. Проводим центральные оси xci , yci для каждого элемента параллельные вспомогательным осям.
и заносим в табл. 5.1. Проводим центральные оси xci , yci для каждого элемента параллельные вспомогательным осям.
x' |
|
y' |
0; x' |
z |
01 |
z |
02 |
2,52 4,3 6,82см; |
||||
c1 |
|
c1 |
|
c2 |
|
|
|
|||||
yc' |
|
|
h |
z02 |
30 |
4,3 |
10,7см. |
|||||
2 |
|
|
|
|
|
|||||||
2 |
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
||||
3. Используя формулы (5.3), определяем координаты центра тяжести всего сечения в системе вспомогательных осей X ,Y
' |
S y |
|
F 1 |
x' |
F 2 |
x' |
31,4 |
6,82 |
|
|
|
|
|
c1 |
|
c2 |
|
|
|
|
|
xc |
|
|
|
|
|
|
|
|
|
2,98см; |
F |
|
|
F 1 |
F 2 |
|
40,5 |
31,4 |
|||
|
|
|
|
|
||||||

|
|
|
|
|
77 |
|
|
|
|
|
' Sx |
|
F 1 |
yc' 1 |
F 2 |
yc' |
2 |
31,4 10,7 |
|
||
yc |
|
|
|
|
|
|
|
|
|
4,67см. |
F |
|
|
F 1 |
F 2 |
|
|
40,5 31,4 |
|||
|
|
|
|
|
|
|||||
Через центр тяжести С составного сечения проводим центральные оси сечения X c ,Yc , параллельные вспомогательным осям. Заметим, что центр тяжести С составного сечения должен лежать на прямой С1С2 , соединяющей центры тяжести швеллера и уголка, что можно использовать для проверки правильности определения положения центра тяжести сложного сечения. Определяем координаты центров тяжести уголка и швеллера в системе центральных осей X c ,Yc и заносим их табл. 5.1.
4. Пользуясь таблицами сортамента прокатной стали [1], устанавливаем осевые и центральные моменты инерции швеллера и уголка относительно собственных центральных осей, и заносим их значения в табл. 5.1. Для равнобокого уголка, который повернут на 90 относительно положения, указанного в сортаменте (рис. 5.4), находим
относительно положения, указанного в сортаменте (рис. 5.4), находим
yc2 |
|
|
|
y2 |
|
|
|
z02 |
c2 |
45° |
x |
|
|
c2 |
|
|
|
|
x2 |
|
|
|
Рис. 5.4 |
|
J xc22 J yc2 |
2 774см4 , |
Jmax2 |
J x22 1229см4 , |
|
Jmin2 |
J y22 |
319см4. |
||
Для определения центробежного момента инерции уголка относительно осей X c2 ,Yc2 воспользуемся одной из формул (5.8) преобразования момента инерции при повороте осей координат. Учитывая, что оси X 2 ,Y2

78
главные (ось X2 является осью симметрии уголка) и, следовательно, J x22 y2 =
, а угол |
= 45 , получим |
|
|
|
|
|
||
J xc2 |
|
J x22 |
J y22 |
sin 2 |
J x22 y2 |
cos 2 |
1229 312 |
|
2 yc2 |
|
2 |
|
2 |
||||
|
|
|
|
|
|
|||
sin(2 45 ) |
455см4. |
|
|
|
|
|||
5. Пользуясь формулами преобразования моментов инерции при параллельном переносе осей координат (5.7), определяем осевые и центробежные моменты инерции швеллера и равнобокого уголка относительно центральных осей X c ,Yc всего сечения.
|
J 1 |
J |
1 |
|
( y' |
y' |
)2 |
F 1 |
5810 |
( |
4,67)2 |
40,5 |
6692,9см4 ; |
||||||||
|
xc |
|
xc1 |
|
c1 |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J 1 |
|
J |
1 |
|
(x' |
|
x' |
)2 |
F 1 |
|
327 |
( |
2,98)2 |
40,5 |
686,6см4; |
|||||
|
yc |
|
yc1 |
|
c1 |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
1 |
J |
1 |
|
|
( y' |
|
|
y' |
) (x' |
|
x' |
) |
F 1 |
0 |
( |
4,67)( 2,98) 40,5 |
||||
xcyc |
xc1yc1 |
|
c1 |
|
|
|
c |
|
|
c1 |
|
c |
|
|
|
|
|
|
|||
|
559,4см4 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
J 2 |
|
J |
2 |
|
( y' |
|
|
y |
' )2 |
F 2 |
|
|
774 |
6,032 |
31,4 |
1915,7см4; |
||||
|
xc |
|
|
xc2 |
c2 |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|||
|
J yc2 |
|
J yc2 |
2 |
(xc' |
2 |
|
|
xc' )2 |
F 2 |
|
774 |
3,842 |
31,4 |
1237см4 ; |
||||||
J |
2 |
J |
2 |
|
|
( y' |
|
|
|
y' |
) |
(x' |
|
|
x' ) F 2 |
455 6,03 3,84 31,4 |
|||||
|
xcyc |
|
xc2 yc2 |
c2 |
|
|
|
c |
|
c2 |
|
|
c |
|
|
|
|
|
|||
1182,1см4 ;
Результаты вычислений заносим в табл. 5.1.
6. Суммируя соответственно осевые и центробежные моменты инерции швеллера и равнобокого уголка относительно центральных осей всего сечения, рассчитываем осевые и центробежный моменты инерции составного сечения относительно его центральных осей X c ,Yc .
Вычисление проводим, используя табл. 5.1.
7. Используя формулу (5.9) определим положение главных центральных осей инерции сложного сечения относительно произвольных центральных осей X c ,Yc
tg2 |
|
|
2J xcyc |
|
|
2 1741,5 |
|
0,521, |
||
0 |
|
J yc |
J xc 1923,6 |
8608,6 |
|
|||||
|
|
|
|
|
||||||
|
|
2 0 |
27 30 , |
0 |
13 45 . |
|
||||
Так как угол 0 |
, то откладываем его от оси X c по ходу часовой |
|||||||||
стрелки. Проводим главные центральные оси инерции X,Y. Ось Х повернута

79
относительно оси X c на угол 13 45 по ходу часовой стрелки, а ось Y пер-
по ходу часовой стрелки, а ось Y пер-
пендикулярна оси Х.
8. По формуле (5.10) рассчитываем значения главных центральных моментов инерции сечения
|
|
|
J xc |
J yc |
1 |
|
|
|
|
|
|
|
|
|||
Jmax, |
|
|
J xc |
J yc 2 |
4J xcyc2 |
|||||||||||
|
2 |
|
|
|
2 |
|
|
|||||||||
|
min |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
8608,6 |
4923,6 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
8608,6 |
1923,6 2 |
4 1741,5 2 . |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как J xc |
J yc , то ось с максимальным моментом инерции должна |
|||||||||||||||
составлять |
с осью |
X c |
меньший угол. Следовательно, в данном случае |
|||||||||||||
J x Jmax |
|
9034,4см4 |
J y |
Jmin 1497,8см 4. |
|
|
|
|||||||||
Проверка Для проверки решения воспользуемся условием неизменности сумм
осевых моментов инерции при повороте осей координат
J x J y J xc J yc;
9034,4 + 1497,8 = 8608,6 + 1923,6 = 10532,2 см 4 .

|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.1 |
|
|
|
|
Результаты вычислений моментов инерции составного сечения |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Но- |
Пло- |
Координаты центра тяжести эле- |
|
Моменты инерции элемента, см |
4 |
|
||||||||
щадь |
|
мента, |
см |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
эле- |
|
|
|
|
|
|
|
|
|
|
|||
мер |
Относительно |
Относительно цен- |
Относительно собственных |
Относительно центральных осей |
||||||||||
мента |
вспомогатель- |
тральных осей се- |
центральных осей |
|
сечения |
|
||||||||
|
|
|
||||||||||||
эле- |
Fi , |
ных осей |
|
чения |
|
|
|
|
|
|
|
|
||
мен- |
см 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x' |
y' |
x' |
x' |
y' |
y' |
J xci |
J yci |
J xciyci |
J xc |
J yc |
J xcyc |
||
та |
|
|||||||||||||
|
ci |
ci |
ci |
c |
ci |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
40,5 |
0 |
0 |
-2,98 |
-4,67 |
5810 |
327 |
0 |
6692,9 |
686,6 |
559,4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
31,4 |
6,82 |
10,7 |
3,84 |
6,03 |
774 |
774 |
455 |
1915,7 |
1237 |
1182,1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
все- |
71,9 |
2,98 |
4,67 |
|
|
|
|
|
|
|
8608,6 |
1923,6 |
1741,5 |
|
го |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сече- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Для проверки можно также воспользоваться одной из формул (5.8),
учитывая что J xy 0, а угол 0 |
13 45 отсчитывается от оси Х против |
хода часовой стрелки
6.ПРЯМОЙ ИЗГИБ
6.1.Общие понятия и расчетные зависимости
6.1.1.Расчеты на прочность при изгибе
Под изгибом понимают такой вид деформирования, при котором в поперечном сечении бруса действует изгибающий момент.
Брус, работающий в основном на изгиб, называют балкой.
Если все внешние силы и пары сил, изгибающие балку, лежат в одной плоскости (силовая плоскость), проходящей через продольную ось балки Z и одну из главных центральных осей инерции поперечного сечения, то изгиб называется прямым. При прямом изгибе ось изогнутой балки располагается в силовой плоскости.
Если в поперечных сечениях балки действуют только изгибающие моменты, то изгиб называется чистым.
При поперечном изгибе в поперечных сечениях балки возникают по-
перечная сила Qy и изгибающий момент M x (рис. 6.1). |
|||
|
y |
P |
P |
|
|
|
|
|
|
Qy |
|
|
|
|
x |
z |
|
Mx |
|
|
|
|
|
|
|
Рис. 6.1 |
|

82
При решении задач, связанных с расчетом на прочность при изгибе, важно научиться правильно определять поперечную силу Qy и изгибающий
момент M x в поперечном сечении балки и строить эпюры этих внутренних
силовых факторов.
Обычно решение задачи начинается с определения опорных реакций (если в этом есть необходимость). Для этого необходимо составить уравнения равновесия. Для балки, нагруженной системой сил, лежащих в одной плоскости, в общем случае можно записать три уравнения равновесия. Определив реакции опор, обязательно делают проверку правильности их определения. Для этого составляют дополнительное уравнение равновесия. Если реакции определены верно, это уравнение удовлетворяется тождественно.
Далее разбивают балку на участки. Границами участков являются: 1) сечения в которых приложены сосредоточенные силы; 2) сечения в которых приложены сосредоточенные моменты; 3) сечения, в которых происходит резкое изменение интенсивности распределенной нагрузки. В пределах каждого участка аналитические выражения Qy и M x остаются неизменными.
Рассматривая произвольное поперечное сечение на каждом участке, используют метод сечений и записывают уравнения для поперечной силы и изгибающего момента. Согласно методу сечений поперечная сила Qy в се-
чении балки равна алгебраической сумме проекций на вертикальную ось всех внешних сил, действующих по одну сторону от рассматриваемого сечения
|
n |
|
Qy |
Pyi. |
(6.1) |
|
i 1 |
|
Изгибающий момент M x в сечении балки численно равен алгебраи-
ческой сумме моментов всех внешних сил относительно центра тяжести рассматриваемого сечения, действующих на отсеченную часть балки
|
n |
|
M x |
mxi. |
(6.2) |
|
i 1 |
|
При этом вводятся следующие правила знаков для Qy и M x . Внеш-
няя сила Р, поворачивающая отсеченную часть балки относительно рассматриваемого сечения по часовой стрелке, дает положительную поперечную силу (положительное слагаемое в выражении для Qy ), и наоборот (рис. 6.2).
Внешний момент m дает положительный изгибающий момент (положительное слагаемое в выражении для M x ), если ось балки при изгибе имеет положительную кривизну (см. рис. 6.2) и наоборот.

83
Поперечная сила Qy , изгибающий момент M x и интенсивность рас-
пределенной нагрузки q связаны дифференциальными зависимостями Д.И.Журавского
dQy |
q, |
dM x |
Qy , |
d 2M x |
q, |
(6.3) |
|
dz |
dz |
dz2 |
|||||
|
|
|
|
где z – координата, определяющая положение сечения балки.
P |
|
Qy |
|
+ |
|
|
|
|
|
|
|
|
|
P |
|
m |
M x |
- |
m |
|
|
|
Рис.6.2
При построении эпюр Qy , M x и их контроле следует учитывать
следствия, вытекающие из дифференциальных зависимостей (6.3) и непосредственно из метода сечений [1].
Построив эпюры поперечных сил и изгибающих моментов, определяют положение опасного с точки зрения прочности сечения балки (если балка имеет постоянное по ее длине сечение, то это сечение, в котором изгибающий момент достигает наибольшего по абсолютной величине значения). Расчет на прочность балок обычно проводят, используя условие прочности по нормальным напряжениям
max |
M x |
, |
(6.4) |
|
|
|
|||
Wx |
||||
|
|
|||
84
где max M x - изгибающий момент в опасном сечении; Wx - осевой момент сопротивления сечения; 
 - допустимое напряжение для материала балки.
- допустимое напряжение для материала балки.
Исходя из условия (6.4), выполняются следующие виды расчета: проверочный, проектный и расчет грузоподъемности.
6.1.2. Определение перемещений при изгибе и расчеты на жесткость 6.1.2.1. Перемещения при изгибе. Условия жесткости При прямом изгибе балки ее ось, искривляясь, остается в силовой
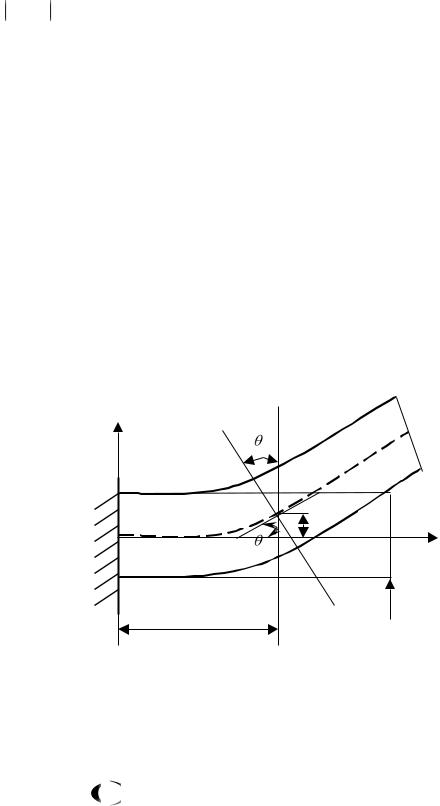
плоскости. Изогнутая ось балки, представляющая собой геометрическое место центров тяжести поперечных сечений деформированной балки, называется упругой линией. Деформация балки в плоскости yz характеризуется двумя перемещениями (рис. 6.3):
y |
|
y |
z |
z |
P |
Рис.6.3
1)прогибом y - линейным перемещением точек оси балки по нормали к ее первоначально прямой оси;
2)углом поворота сечения 
 - углом, на который поворачивается по-
- углом, на который поворачивается по-
перечное сечение балки относительно его первоначального положения, так как по гипотезе Бернулли поперечное сечение остается плоским и перпенди-

|
|
|
|
|
|
85 |
|
|
кулярным изогнутой оси балки. Из этой же гипотезы следует, что |
y , где |
|||||||
y |
y z |
- уравнение упругой линии (см. рис.6.3). |
|
|||||
|
При эксплуатации элементов конструкций перемещения y и |
долж- |
||||||
ны быть ограничены по величине и удовлетворять условиям жесткости |
|
|||||||
|
|
|
y |
|
y ; |
|
, |
(6.6) |
|
|
|
|
|
||||
где |
y и |
– допускаемые значения прогиба и угла поворота, задаваемые |
||||||
из конструктивных и технологических соображений. Из условий жесткости (6.6) выполняют те же виды расчетов, что и из условия прочности (6.4).
6.1.2.2. Определение перемещений интегрированием дифференциального уравнения упругой линии балки. Метод начальных параметров
Дифференциальное уравнение упругой линии балки при малых перемещениях
y |
M x |
|
, |
(6.7) |
|||
EI x |
|||||||
|
|
|
|
||||
где M x - изгибающий момент, EI x - жесткость балки. |
|
||||||
Уравнение углов поворота |
|
|
|
|
|
|
|
y |
|
M x |
dz C. |
(6.8) |
|||
|
|
||||||
|
|
EI x |
|
|
|
||
Уравнение упругой линии
y |
M x |
dz dz Cz D. |
(6.9) |
|
EIx |
||||
|
|
|
Если балка состоит из n участков, то уравнение углов поворота и упругой линии представляются в виде
|
yk |
|
M xk |
|
dz Ck ; |
(6.10) |
|
k |
|
EI x |
|
||||
|
|
|
|
k |
|
||
yk |
|
M xk |
dz |
dz Ck z Dk . |
(6.11) |
||
|
(EI x )k |
||||||
|
|
|
|
|
|
||
где k = 1,2,…,n.
Постоянные Сk , Dk , число которых равно 2n, определяют из условий
закрепления (два условия для статически определимых балок) и условия непрерывности и плавности упругой линии балки. Отсюда следует, что в смеж-
