
Сопротивление материалов. Теория и практика. Воропаев А.А., Попов С.П
.pdf
36
А.А.Воропаев С.П.Попов С.И.Свиридов Ф.Х.Томилов Д.В.Хван
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ. ТЕОРИЯ И ПРАКТИКА
Учебное пособие
τ
τmax
σ3 |
σ |
|
σ2
σ1
Воронеж 2001
37
УДК 539.3/7
Воропаев А.А. Сопротивление материалов. Теория и практика: Учеб. пособие / А.А.Воропаев, С.П.Попов, С.И.Свиридов, Ф.Х.Томилов, Д.В.Хван; Под ред. С.П.Попова. Воронеж: Изд-во ВГТУ, 2001. с.
В учебном пособии в конспективном виде приведены теоретические сведения по основным разделам курса «Сопротивление материалов, а также рассмотрены подробные примеры решения типовых задач.
Издание предназначено для студентов заочного обучения механических специальностей технических университетов и академий.
Учебное пособие подготовлено на магнитном носителе в текстовом редакторе MS WORD 97.0 и содержится в файле «Сопромат.rar»
Табл. 5. Ил. 86. Библиогр.: 8 назв.
Научный редактор канд. техн. наук В.Н.Потапов
Рецензенты: кафедра технической механики Воронежской государственной технологической академии;
д-р техн. наук Ю.А.Цеханов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© Воропаев А.А., Попов С.П., Свиридов С.И., Томилов Ф.Х., Хван Д.В., 2001
©Оформление. Издательство Воронежского государственного технического университета, 2001
38
ПРЕДИСЛОВИЕ
Настоящее учебное пособие составлено в соответствии с программой курса «Сопротивление материалов» для механических специальностей вузов и имеет целью оказать помощь студентам заочного обучения в овладении материалом основных разделов курса и методами решения типовых задач.
Впособии приведены краткие сведения из теории, а также основные справочные данные, позволяющие с минимальной затратой времени восстановить в памяти и систематизировать ранее изученный материал.
Вкаждом из разделов пособия приведены примеры решения типовых задач. Разбор примеров дан с необходимыми подробными пояснениями и каждое решение доведено до числового результата, что способствует развитию у студентов навыков решения задач и грамотного оформления технических расчетов.
Вконце пособия приведен список литературы, использованной при подготовке данного учебного пособия.
39
1.ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ
1.1.Основные задачи курса сопротивления материалов
Сопротивление материалов – инженерная дисциплина о прочности, жесткости и устойчивости элементов конструкций. Под прочностью понимается способность элемента конструкции сопротивляться эксплуатационным нагрузкам без разрушения. Под жесткостью понимается способность элемента конструкции сопротивляться эксплуатационным нагрузкам без недопустимых изменений его формы и размеров. Здесь следует заметить, что если в теоретической механике тела принимаются как абсолютно жесткие, то в сопротивлении материалов тела рассматриваются как деформируемые, то есть, учитывается, что под действием внешних сил (нагрузок) тело меняет свою форму и размеры (деформируется).
Рассмотрим в качестве примера колесо турбины. Если колесо недостаточно прочное, то под действием возникающих при его вращении сил инерции оно разрушится. Если же колесо недостаточно жесткое, то под действием инерционных нагрузок диаметр турбинного колеса возрастет настолько, что его лопатки начнут задевать корпус, в результате чего конструкция также потеряет свою работоспособность.
Под устойчивостью понимается способность элемента конструкции сохранять свое первоначальное состояние упругого равновесия под действием эксплуатационных нагрузок.
Вкачестве второго примера рассмотрим прямолинейную стойку большой длины и малого сечения, нагруженную вдоль еѐ оси сжимающей силой. Если под действием этой силы стойка не разрушилась, то это означает, что она прочная. Если под действием нагрузки укорочение стойки, вследствие еѐ деформации, не превышает допустимой величины, то, следовательно, она жесткая. Если же в результате действия нагрузки ось стойки осталась прямой (не изогнулась), то, значит, стойка является устойчивой.
Всопротивлении материалов рассматриваются экспериментальные и теоретические основы методов расчета элементов конструкций на прочность, жесткость и устойчивость. В то же время рассчитываемый конструктивный элемент должен соответствовать требованиям экономичности, связанным с металлоемкостью. Повышение прочности, жесткости и устойчивости достигается, как правило, увеличением расхода материала и, следовательно, веса конструкции, что приводит в итоге к еѐ удорожанию. Следовательно, при выполнении расчетов необходимо соблюдать разумный компромисс между взаимно противоречивыми требованиями прочности, жесткости и устойчивости с одной стороны и экономичности – с другой.
40
Таким образом, основными задачами, рассматриваемыми в курсе сопротивления материалов, являются задачи расчета на прочность, жесткость и устойчивость, в результате решения которых определяются надежные размеры элементов конструкций.
1.2. Расчетная схема
Реальные элементы конструкций обладают, как правило, большой сложностью. Однако многие конструктивные и другие особенности этих элементов либо вообще не влияют, либо оказывают слабое влияние на результаты их расчетов на прочность, жесткость и устойчивость. Поэтому при выполнении расчетов можно рассматривать не сам конструктивный элемент,
аего идеализированную (упрощенную) модель, так называемую расчетную схему.
Расчетной схемой называют реальный объект, освобожденный от особенностей, несущественных с точки зрения их влияния на прочность, жесткость и устойчивость. Введение расчетной схемы объясняется необходимостью упрощения решаемой задачи и касается как самого рассчитываемого объекта, то есть его конструктивных особенностей, так и свойств материала, из которого он изготовлен, а также характера нагружения. Таким образом, в сопротивлении материалов рассматриваются не сами элементы конструкций,
аих расчетные схемы. Переход от реальных объектов к расчетным схемам не является задачей сопротивления материалов, это задача специальных дисциплин, таких как расчет на прочность, жесткость и устойчивость станков, самолетов, кораблей, строительных конструкций и т.п.
Расчетная схема – это идеализированный (упрощенный) объект расчета. Идеализируются прежде всего геометрия рассчитываемого объекта и свойства его материала.
1.2.1.Предмет изучения сопротивления материалов
Идеализация геометрии сводится к тому, что конструктивные элементы приводят к схемам бруса, оболочки или массива.
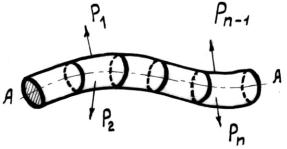
Под брусом понимают тело, у которого один из размеров (длина) значительно больше других характерных размеров. На (рис. 1.1) схематично показан брус, осью которого является линия АА . Сечения, перпендикулярные к оси бруса, называются поперечными. Ось бруса – геометрическое место центров тяжести его поперечных сечений. Если ось прямая, то брус называют прямым, если изогнута - кривым. Если поперечное не изменяется по длине бруса, то его называют брусом постоянного сечения. В противном случае –
41
брусом переменного сечения. Примерами брусьев являются стойки, колонны, валы, балки перекрытий.
Оболочкой называют тело, у которого один из размеров (толщина) существенно меньше двух других размеров. Примерами оболочек являются мембраны, сосуды, котлы, крыло самолета, корпусные детали.
Рис. 1.1
Массивом называют тело, у которого все размеры одного порядка. К массивам относятся основания и фундаменты зданий, шарик подшипника и др. Это наиболее сложные для расчета тела.
Предметом изучения курса сопротивления материалов в основном является брус. Рассматриваются также некоторые задачи расчета оболочек. Массивы являются объектами изучения специальных дисциплин и в сопротивлении материалов вообще не рассматриваются.
1.2.2. Рабочие гипотезы сопротивления материалов.
Попытка учесть в расчетах все многообразие физических свойств материала привела бы к исключительным математическим трудностям. Поэтому в сопротивлении материалов при сохранении основных свойств материала сознательно упрощаются его отдельные свойства и все расчеты строятся на использовании ряда упрощающих гипотез, получивших название рабочих. В соответствии с этими гипотезами материал считается сплошным, однородным, изотропным и идеально упругим.
Гипотеза сплошности предполагает непрерывное заполнение материалом геометрического объема детали. В действительности же в некоторых материалах могут быть пустоты, каверны, раковины, трещины. Однако их влияние не учитывается в расчетах. Использование этой гипотезы позволяет применить анализ бесконечно малых, то есть аппарат дифференциального и интегрального исчисления.
Гипотеза однородности предполагает одинаковость свойств материала во всех точках тела. В действительности же свойства поверхностных слоев
42
детали иногда могут отличаться от свойств ее сердцевины (например, у литой детали или детали, прошедшей поверхностную термообработку). Но для большинства материалов эта гипотеза однородности свойств материалов оказывается вполне приемлемой.
Гипотеза изотропности предполагает одинаковость свойств материалов по всем направлениям, то есть материал считается изотропным. Большинство материалов соответствуют этой гипотезе, но некоторые из них обладают начальной (исходной) анизотропией (например, дерево, у которого свойства вдоль волокон отличны от свойств в направлении поперечном к волокнам). Такие материалы, у которых свойства зависят от направления, называют анизотропными. Анизотропия может быть и приобретенной, наведенной в ходе механической обработки материала. Например, сильной анизотропией обладает листовой прокат из титана, алюминиевых и алюминиево-литиевых сплавов.
Гипотеза идеальной упругости предполагает, что после снятия нагрузки тело полностью восстанавливает свою форму и размеры. Таким образом, считается, что материал обладает свойством упругости и остаточные (пластические) деформации в разгруженном после деформирования теле отсутствуют, то есть материал ведет себя подобно резине. В действительности же большинство материалов деформируются упруго только до определенного предела и если этот предел превзойти, то в нем появляются остаточные деформации. Так как большая часть элементов конструкций работает, как правило, при упругих деформациях, то эта гипотеза также оказывается приемлемой.
Следует заметить, что в последнее время, при выполнении отдельных расчетов учитываются и пластические свойства материалов.
1.3. Силы внешние и внутренние. Напряжения 1.3.1. Классификация нагрузок
Внешние силы, действующие на элемент конструкции, называют нагрузками. Рассмотрим их классификацию.
По геометрии области приложения нагрузки делят на сосредоточенные и распределенные.
Сосредоточенной называют нагрузку, область приложения которой настолько мала, что еѐ можно считать приложенной в точке. Это тоже в известном роде идеализация, так как в природе сосредоточенных нагрузок не существует, потому что в зоне контакта твердые тела деформируются и в связи с этим передача усилия осуществляется по какой-то площадке, пусть малых, но конечных размеров. Единицей измерения сосредоточенной нагрузки, если

43
это сила, служит Н , если это момент (пара сил), то соответственно Нм и их производные.
Нагрузка, не попадающая под определение сосредоточенной, называется распределенной. Количественной мерой такой нагрузки является еѐ интенсивность q . Распределенные нагрузки делят на три группы: распределенные по длине, по площади и по объему. Примером нагрузки распределенной по длине может служить собственный вес провода, вес его оледенения, размерность q H / м .
Нагрузки, распределенные по площади, называют поверхностными. Примерами таких нагрузок является давление пара на поршень, воздуха на
крыло самолета, размерность q H / м2 .
Нагрузки, распределенные по объему, называют массовыми (действуют они на каждую частицу массы тела). Примерами таких нагрузок являются силы тяжести, силы инерции, силы магнитного притяжения, размерность q H / м3 .
По характеру изменения во времени нагрузки делят на статические, динамические и циклические. К статическим относятся нагрузки постоянные во времени или изменяющиеся настолько медленно, что возникающие при этом силы инерции не оказывают существенного влияния на прочность, жесткость и устойчивость элемента конструкции. Примером статической нагрузки может служить вес самого элемента конструкции.
Нагрузки, изменяющиеся во времени с большой скоростью, относят к динамическим. Возникающие при этом значительные силы инерции необходимо учитывать при выполнении расчетов на прочность, жесткость и устойчивость. Примерами динамических нагрузок служат забивание свай, удар тела о преграду, ковка на молотах, взрывная штамповка.
Циклическими называют нагрузки, периодически повторяющиеся во времени. Примером такой нагрузки является давление пара на шток поршня.
1.3.2. Внутренние силы. Метод сечений
Действию нагрузок на тело противостоят силы внутреннего сопротивления, силы взаимодействия между отдельными его частями, которые называют внутренними силами. По мере роста внешних сил внутренние силы тоже возрастают и при некоторой величине нагрузок они могут превзойти силы сцепления частиц материала, что приводит к его разрушению. Опыт показывает, что разрушение начинается в том месте, где внутренние силы, обусловленные нагрузками, достигают наибольшей величины. Поэтому для оценки
44
прочности, жесткости и устойчивости элемента конструкции необходимо определить внутренние силы.
Как и в теоретической механике, в сопротивлении материалов внутренние усилия определяют методом сечений. Метод сечений заключается в мысленном разделении тела на части с целью определения величины внутренних усилий. При этом считается, что если рассматриваемое тело находится под действием нагрузок в равновесии, то в равновесии должна находиться и любая выделенная из него часть.
Допустим, что некоторый произвольный брус (см. рис. 1.1) находится в равновесии под действием системы внешних сил, в которую входят как активные силы (нагрузки), так и реакции связи. Разрежем мысленно этот брус плоскостью, совпадающей с поперечным сечением, на две части и также мысленно отбросим одну из частей. В месте разреза высвободятся силы взаимодействия между отброшенной и оставшейся частями, то есть внутренние силы. В соответствии с законом о равенстве действия и противодействия внутренние силы будут взаимны, то есть равны по величине и противоположны по направлению, поэтому безразлично какую из частей рассматривать при определении интегральной величины внутренних усилий.
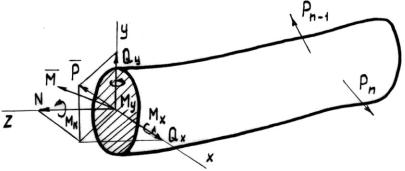
Согласно гипотезе сплошности материала внутренние силы непрерывно распределяются по всей поверхности сечения. Рассмотрим отсеченную правую часть бруса и введем в рассмотрение декартову систему координат X, Y, Z, начало которой совместим с центром тяжести сечения (рис. 1.2). Ось Z направим по касательной к оси бруса, а оси X, Y расположим в плоскости рассматриваемого поперечного сечения. Возникающую в этом сечении систему внутренних сил, как известно из теоретической механики, можно привести к главному вектору Р и главному моменту М, которые в общем случае произвольно ориентированны в пространстве. Проектируя главный вектор и главный момент на оси выбранной системы координат, получим три силы: нормальную (продольную) N и две поперечные Qx и Qy, а также три момента: крутящий Мк и два изгибающих Мх и Му (см. рис. 1.2). Эти шесть составляющих называются внутренними силовыми факторами в сечении бруса. Их величину можно определить через значения внешних сил из шести уравнений равновесия, которые можно составить для рассматриваемой отсеченной части бруса.
Х |
0; |
Y |
0; |
Z |
0; |
mx |
0; |
my |
0; |
mz |
0. |
(1.1)
45
Рис. 1.2
Внутренние силовые факторы вдоль оси бруса могут меняться как по величине, так и по направлению. Для выявления наиболее нагруженного сечения строят графики (эпюры) внутренних усилий. В зависимости от характера нагружения бруса в его сечениях могут возникать либо все шесть внутренних силовых факторов, либо только некоторые из них, например, только нормальная сила и изгибающий момент и т.д. В соответствии с тем, какие из внутренних силовых факторов оказываются отличными от нуля, различают тот или иной вид деформирования.
1.3.3. Классификация видов деформирования
Внутренние силовые факторы имеют ярко выраженный физический смысл. Каждому из них соответствует определенный вид деформирования.
Если в поперечном сечении бруса возникает только нормальная сила (N≠0), то в зависимости от направления этой силы деформирование называют растяжением или сжатием.
Если в поперечном сечении бруса действует только крутящий момент (Мк≠0), то деформирование называют кручением.
Если в поперечном сечении бруса возникает только изгибающий момент (Мх≠0 или Му≠0), то деформирование называют чистым изгибом.
Если в поперечном сечении бруса возникает только поперечная сила (Qy≠0 или Qx≠0), то деформирование называют сдвигом (срезом).
Перечисленные четыре вида деформирования (сопротивления) называют простыми, всякое их сочетание называют сложным деформированием (сложным сопротивлением).
1.3.4. Напряжения
