Основы механики. Рябцев В.А., Воропаев А.А

ком сложен и почти всегда связан математическими трудностями. Вовторых, чаще всего, бывает достаточно определить некоторые общие характеристики движения системы, а не движение каждой из ее точек в отдельности. Эти общие характеристики и определяются с помощью общих теорем динамики системы.

13.2. Теорема о движении центра масс Часто для описания движения системы (особенно твердого

тела), достаточно знать закон движения ее центра масс. Из (16.1) следует

Поскольку M mk - масса системы, из (13.2) следует

mkrk MrC .

Считая массы точек постоянными и дифференцируя дважды это равенство по времени, получим

где ac - ускорение центра масс системы.

Поскольку для внутренних сил системы Fki 0, из

(16.2), получим

Соотношение (13.4) и выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно главному вектору всех действующих на систему внешних сил. Сравнивая (13.4) с уравнением движения материальной точки (8.3), получаем другое выражение теоремы: центр масс системы движется как материальная точка с массой, равной массе системы, и к которой приложены все внешние силы, действующие на систему.

180

Проецируя (13.4) на координатные оси, получим дифференциальные уравнения движения центра масс системы в проекциях на оси декартовой системы координат

Важность доказанной теоремы состоит в следующем.

1)Теорема дает обоснование методов динамики точки, поскольку решение уравнений (13.5), получаемое, в предположении, что данное тело является материальной точкой, определяет закон движения центра масс этого тела.

В частности, если тело движется поступательно, то его движение полностью определяется движением центра масс. Поэтому поступательно движущееся тело можно всегда считать материальной точкой с массой, равной массе тела. В остальных случаях тело можно рассматривать как материальную точку лишь тогда, когда положение тела можно определить положением его центра масс.

2)Практическая ценность теоремы состоит в том, что она позволяет не учитывать влияние всех априорно неизвестных внутренних сил при определении закона движения центра масс системы.

13.3. Закон сохранения движения центра масс Из теоремы о движении центра масс можно получить сле-

дующие важные следствия.

1) Пусть сумма внешних сил, действующих на систему,

равна нулю Fke 0. Тогда из уравнения (13.4) следует, что

aC 0 или vC const .

Следовательно, если сумма всех действующих на систему внешних сил равна нулю, то центр масс этой системы движется с постоянной скоростью, т. е. равномерно и прямолинейно. В частности, если вначале центр масс был в покое, то он и останется в покое. Очевидно, что внутренние силы, не могут изменить движение центра масс системы.

181

2) Пусть сумма внешних сил, действующих на систему, не равна нулю, но сумма их проекций на некоторую ось (напри-

мер, ось Ох) равна нулю: Fkxe 0. Тогда первое из уравне-

ний (13.5) примет вид xC 0 или xC vCx const .

Следовательно, если сумма проекций всех действующих внешних сил на некоторую ось равна нулю, то проекция скорости центра масс системы на эту ось будет постоянной величиной. В частности, если в начальный момент vCx = 0, то и в

любой следующий момент vCx = 0, т. е. центр масс системы

вдоль оси Ох в этом случае перемещаться не будет (хс = const). Все эти результаты выражают закон сохранения движения центра масс системы. Рассмотрим некоторые примеры, иллю-

стрирующие его приложения.

а) Движение центра масс солнечной системы. Так как притяжением планет солнечной системы звездами можно практически пренебречь, то можно считать, что на солнечную систему внешние силы не действуют. Следовательно, в первом приближении ее центр масс движется в мировом пространстве равномерно и прямолинейно.

б) Действие пары сил на тело. Если на свободное твердое тело действует пара сил ( F и F ), то векторная сумма этих

внешних сил будет равна нулю ( F F 0 ). Следовательно, неподвижный до приложения пары сил центр масс С тела, при действии пары останется в покое. Поэтому, при приложении произвольной пары сил к свободному твердому телу, оно начнет вращаться вокруг своего центра масс.

в) Движение по горизонтальной плоскости. При отсутствии трения человек с помощью своих мускульных усилий (силы внутренние) не мог бы двигаться вдоль горизонтальной плоскости, так как в этом случае сумма проекций на любую горизонтальную ось Ох всех приложенных к человеку внешних сил (сила тяжести и реакция плоскости) будет равна нулю и центр масс человека вдоль плоскости перемещаться не будет

(хс = const).

182

Если, например, человек вынесет правую ногу вперед, то левая его нога скользнет назад, а центр масс тела останется на месте. При наличии же трения скольжению левой ноги назад будет препятствовать сила трения, которая будет направлена вперед. Эта сила и позволит человеку перемещаться в сторону ее действия (в данном случае вперед).

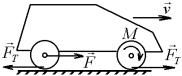
Аналогично происходит движение паровоза или автомобиля. Сила давления пара или газа в двигателе является силой внутренней и сама по себе не может переместить центр масс системы. Движение происходит потому, что двигатель передает соответствующим колесам, называемым ведущими, вращающий момент M . При этом точка касания В ведущего колеса стремится скользить влево. Тогда на колесо будет дейст-

вовать сила трения, направленная вправо. Эта внешняя сила и позволит центру тяжести паровоза или автомобиля двигаться вправо. Когда этой силы нет, или когда она недостаточна для преодоления со-

противления движению, движение не возникнет. При этом возникнет буксование: ведущие колеса будут при этом вращаться, а автомобиль останется на месте.

г) Торможение. Для торможения к барабану, жестко связанному с вращающимся колесом, прижимают тормозную колодку. Возникающая при этом сила трения колодки о барабан будет силой внутренней и сама по себе не изменит движение центра масс, т. е. не затормозит поезд или автомобиль. Однако трение колодки о барабан будет замедлять вращение колеса вокруг его оси и увеличит силу трения колеса о рельс (или грунт), направленную противоположно движению. Эта внешняя сила и будет замедлять движение центра масс поезда или автомобиля, т. е. вызывать торможение.

183

13.4. Решение задач Пользуясь теоремой о движении центра масс, можно, зная

внешние силы, найти закон движения центра масс, и наоборот, зная движение центра масс, определить главный вектор действующих на систему внешних сил. Первая задача рассмотрена в гл. 8. Примеры решения второй задачи рассмотрим ниже.

Теорема о движении центра масс позволяет исключить из рассмотрения все внутренние силы. Поэтому рассматриваемую систему следует выбирать так, чтобы как можно большее количество неизвестных сил стали внутренними.

В случаях, когда выполняется закон сохранения движения центра масс, теорема позволяет по перемещению одной части системы найти перемещение другой ее части.

Выше доказано, что когда Fkxe 0 и в начальный мо-

мент vCx 0, то при движении системы хс= const. Пусть для определенности система состоит из трех тел с массами m1,m2 ,m3 и начальные координаты их центров масс равны x1, x2 , x3 . Если под действием внутренних (или внешних) сил тела совершат абсолютные перемещения, проекции которых на ось Ох равны 1, 2 , 3 , то соответствующие координаты

координаты центра масс xC всей системы в начальном и ко-

нечном положениях определятся выражениями

Следовательно, если в начальный момент центр масс сис-

184

темы неподвижен, то при выполнении закона сохранения движения центра масс вдоль оси Ох сумма произведений масс (или сил тяжести) тел системы на проекции абсолютных перемещений их центров масс должна быть равна нулю. Определяя абсолютные перемещения i , сле-

дует учитывать их знаки.

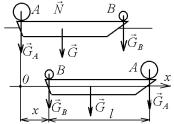
Задача 13.1. На носу и корме лодки массой M сидят на расстоянии l друг от друга два человека весом mA и mB . Пренебрегая сопротивлением воды, определить, куда и насколько переместится лодка, если люди поменяются местами.

Решение. Чтобы исключить из рассмотрения неизвестные силы трения обуви о дно лодки и мускульные усилия людей, будем рассматривать лодку и людей как одну систему (при этом указанные силы станут внутренними). Внешними силами, действующими на систему, будут вертикальные силы

G,GA,GB , N . Тогда Fkxe 0 и, так как в начальный момент vC 0, то xCx const . Следовательно, абсолютные перемеще-

ния всех тел связаны зависимостью (13.6).

Далее следует изобразить лодку и людей в конечных положениях. Рекомендуется независимо от того, куда фактически происходит смещение, изображать лодку (систему) в смещенном положении так, чтобы координата ее центра масс была положительной. Если после вычислений х получится отрицательным, то это будет означать, что смещение происходит в другую сторону.

По определению перемещение лодки л x1 . Абсолютное перемещение первого человека A x l ; абсолютное перемещение второго человека равно BB1, а проекция этого пере-

185

мещения на ось Ох будет равна B l x . Тогда из (13.7)

получим Mx mA x l mB (l x) 0.

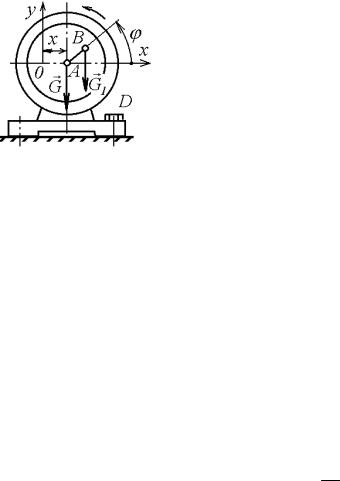
тор, поставленный на гладкую горизонтальную плоскость, когда вал вращается с постоянной угловой скоростью . Найти дополнительно максимальную силу, которая будет действовать на болт D, неподвижно закрепляющий мотор.

Решение. Чтобы исключить силы, вращающие вал, сделав их внутренними, рассмотрим весь мотор как одну систему.

При незакрепленном моторе все действующие на него силы тяжести G1 m1g , G2 m2g и реакция плоскости будут вертикальными и, как и в предыдущей задаче, будет выполняться закон сохранения движения центра масс вдоль оси Ох. Изображаем мотор в произвольном положении (рис. 16.3), считая начальным то положение, когда точки В и А лежат на одной вертикали (на оси Оу). Тогда в произвольном положении A x, B x a sin . Учитывая, что t , из (13.6)

получим m2 m1(x asin t ) 0, откуда x m1 asin t , где

M

M m1 m2 .

186

Следовательно, мотор будет совершать гармонические колебания с круговой частотой .

2) Когда мотор закреплен, то из первого из уравнений (16.5) горизонтальная реакция Rx болта будет равна

Rx MxC , где xC (m2xA m1xB )/ M .

В этом случае точка А неподвижна и xA h=const , xB h asin t . Дифференцируя х и умножая его на М, нахо-

дим Rx MxC m1xB m1a 2 sin t .

Сила давления на болт равна -R.

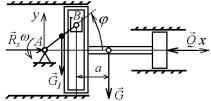
Задача 13.3. Кривошип АВ длиной r и массой m , вращающийся с постоянной угловой скоростью , приводит в движение кулису и связанный с нею поршень D, общая масса которых равна M (рис. 13.4). На поршень

при его движении действует постоянная сила Q. Пренебрегая трением о направляющие, найти наибольшую горизонтальную силу давления на ось А кривошипа.

Решение. Чтобы исключить силы, вращающие кривошип, и силу давления на него со стороны кулисы, рассмотрим движение всей системы. Тогда из первого из уравнений (16.5), если обозначить горизонтальную реакцию оси А через Rx , по-

лучим:

Сила давления на ось равна по модулю R и направлена в противоположную сторону. Ее максимум будет достигнут прии будет равен Q r 2(0,5m M ).

187

13.5.Задачи для самостоятельного решения

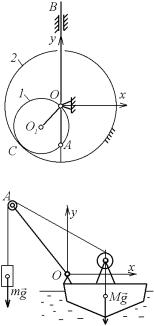
13.5.1.В механизме, изображенном на рис. 13.5, кривошип

OO1 r массой m1 , вращается в вертикальной плоскости вокруг неподвижной оси О с постоянной угловой скоростью и вращает колесо 1 радиуса r и массы m , которое катится без скольжения по неподвижному колесу 2 радиуса 2r . Центр тяжести колеса 1 находится в точке O1 . Стержень АВ массы m2 , соединенный шарниром А с колесом 1, движется поступательно в вертикальных направляющих. Найти проекции импульса этой системы на координатные оси x и y

(рис. 13.5).

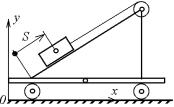
13.5.2.Определить перемещение

кости при помощи лебедки поднимается груз С массой m2 так,

что расстояние АС изменяется по закону s 0,5at2 . В начальный момент вся система находится в покое. Определить скорость, с которой будет двигаться платформа; сопротивлением движению платформы пренебречь.

13.5.4. Мотор, массой M, прикреплен к фундаменту болтами (рис.13.3). Масса ротора мотора равна m , а его центр масс В смещен относительно оси вращения на расстояние AB = e . Ротор вращается по закону 0,5 t2 Определить верти-

188

кальную силу давления мотора на фундамент и горизонтальную силу, действующую на все болты, в момент времени t 1 с.

13.5.5. Человек массы m = 70 кг переходит с кормы на нос лодки. На какое расстояние переместится лодка длиной l= 5 м относительно дна

13.5.6.Человек массы m = 60 кг переходит с носа на корму лодки. На какое расстояние переместится лодка длиной l= 3 м, если ее масса M = 120 кг?

13.5.7.Лодка неподвижно стоит в озере. На корме и на носу лодки на расстоянии L= 5 м друг от друга сидят рыболовы. Масса лодки М= 150 кг , массы рыболовов m1 = 90 кг и m2 = 60 кг. Рыболовы меняютсяместами. Определить перемещение лодки.

13.5.8.Плот массой M = 500 кг и длиной l= 10 м неподвижен в стоячей воде. С противоположных концов плота од-

новременно начали двигаться два человека с массами m1 = 70

кг и m2 = 100 кг. Найти смещение плота в момент, когда человек с меньшей массой пройдет весь плот, а второй - будет на середине.

13.5.9. Снаряд разорвался в верхней точке траектории на высоте H = 100 м на две части массами m1= 1 кг и m2 = 1,5

кг. Скорость снаряда в этой точке v0= 100 м/с. Скорость большего осколка оказалась горизонтальной, совпадающей по направлению с v0 и равной v2 = 250 м/с. Определить расстоя-

ние S между точками падения обоих осколков без учета сопротивления воздуха.

13.5.10. Снаряд, вылетевший из орудия со скоростью vпод некоторым углом к горизонту, разорвался в верхней точке своей параболической траектории на два осколка равных масс. Один осколок после взрыва возвращается к орудию по прежней траектории. Где упадет второй осколок? Упадут ли оба ос-

189