2.3. Математическое описание объектов оптимального проектирования с использованием моделей массового обслуживания

Функционирование сложных систем может быть описано моделями массового обслуживания. Примерами таких процессов являются: сборочно-монтажные работы, контрольные операции на участках серийного производства, работы по обслуживанию и наладке автоматизированного и роботизированного производства. Они характеризуются тем, что имеются случайный поток событий (заявок), поступающих на обслуживание, и операция (канал) обслуживания (обработки), на выполнение которой требуется разное (случайное) время.

Для построения математических моделей экономических систем как систем массового обслуживания (СМО) необходимо описать следующие компоненты: входной поток однородных событий; дисциплину очереди заявок; механизм обслуживания.

Под входным потоком однородных событий будем понимать некоторую последовательность событий, однородных в том смысле, что имеет значение лишь факт наступления или ненаступления события в тот или иной момент времени. Описание потока может быть задано:

- моментами времени наступления событий

- интервалами времени между наступлениями событий

- количеством событий, имевших место на интервале времени

На множестве реализаций потока однородных событий рассмотренные величины являются случайными и могут быть описаны характеристиками:

1) - совместной плотностью распределения;

2) - совместной функцией распределения интервалов времени между наступлением событий;

3) – значениями вероятностей наступления событий на интервале .

Первые два вида описания являются совместными распределениями непрерывных случайных величин и позволяют учитывать корреляцию между моментами наступления событий. Последний вид описания представляет собой распределение дискретной случайной величины, которое может быть задано как в аналитической, так и в табличной формах. Оно является более наглядным и, хотя не позволяет учитывать корреляционные связи между событиями, широко используется при анализе СМО.

Классификация входных потоков осуществляется по следующим признакам: стационарности, ординарности, зависимости наступления от наступления события от предыдущих событий. Поток однородных событий называется стационарным, если вероятность того, что в интервале времени наступит событий, одна и та же для всех :

где T – интервал наблюдений, k-целое число.

Поток однородных событий называется ординарным, если при и при любом постоянном имеет место соотношение

Данная запись означает, что вероятность стремится к 0 быстрее, чем , т.е. ординарность потока представляет собой практическую невозможность совмещения двух или более событий в один и тот же момент времени.

По степени зависимости событий между собой различают потоки с последействием, ограниченным последействием и без последействия. Поток событий называется потоком без последействия, если вероятность наступления определенного числа событий в промежутке времени и не зависит от того, сколько событий и в каком порядке было до момента времени Такой поток описывается одинаковой плотностью распределения для всех интервалов времени между наступлениями событий. Для потока с ограниченным последействием плотность распределения интервала времени до наступления первого события в промежутке времени отличается от остальных и вычисляется по формуле Пальма:

где - средняя плотность потока, т.е. математическое ожидание числа событий в единицу времени.

Выделяют различные типы входных потоков. Наиболее распределенными являются простейшие (пуассоновские) потоки. Поток однородных событий называется простейшим, если он обладает тремя свойствами: стационарностью, ординарностью и отсутствием последействия. Простейший поток описывается пуассоновским законом распределения вероятностей наступления k событий на интервале времени t:

(2.33)

Плотность распределения интервалов времени между наступлениями событий является в этом случае показательной функцией с параметром

(2.34)

Важную роль в сложных системах играют потоки с последействием. На практике стремятся к ритмичности производства, т.е. к регулярным потокам. Регулярность приводит к потокам с ограниченным последействием (потокам Пальма). Частный случай потоков Пальма – это потоки Эрланга, которые, являясь потоками с ограниченным последействием, обладают стационарностью и ординарностью. В зависимости от порядка потока Эрланга v последействие меняется v=0 (отсутствие последействия) до возникновения регулярного потока. Плотность распределения интервалов времени между наступлениями событий для потока Эрланга имеет вид:

(2.35)

Важным понятием систем массового обслуживания является понятие дисциплины очереди заявок. При функционировании СМО различают следующие формы дисциплины очереди заявок:

1) Обслуживание в порядке поступления заявок в систему. При такой дисциплине очереди обслуживается первой та заявка из ожидающих в очереди, которая поступила в систему раньше всех остальных. Примером являются операции по сборке, контролю.

2) Обслуживание заявок в случайном порядке. В очереди находится группа заявок, которые случайным образом выбираются для обслуживания. Примером являются операции, связанные с устранением дефектов на выходе конвейера.

3) Обслуживание с преимуществами (приоритетами). При такой дисциплине каждой заявке, поступающей в систему, приписываются некоторая степень важности или некоторый коэффициент преимущества. Примером являются работы по обслуживанию и наладке автоматизированного производства.

Еще одно понятие - механизм обслуживания. Различают следующие механизм обслуживания:

1) С отказами (если канал обслуживания занят, то заявка уходит из системы). Примером является сборочный конвейер, для которого сборочные единицы, поступившие на рабочее место в момент выполнения операции, возвращаются на склад. Эффективность при ограниченном числе каналов определяется требованием минимальной вероятности отказа.

2) С ожиданием (в такой системе обслуживаются все заявки в соответствии с дисциплиной очереди). Эффективность при ограниченном числе каналов определяется требованием минимального времени ожидания или минимальной длины очереди.

3) С ограничением (смешанный тип обслуживания с установленной длиной очереди). Эффективность оценивается совокупностью показателей, характерных для первого и второго механизмов обслуживания.

Функционирование канала обслуживания определяется временем обслуживания, которое является случайной величиной

Во многих практических случаях время обслуживания подчиняется показательному закону распределения:

(2.36)

где - интенсивность обслуживания (среднее число заявок, об­служиваемых в единицу времени).

По числу каналов различают одноканальные и многоканаль­ные СМО. Если каналы расположены последовательно, то процесс обслуживания в одном канале является одной фазой всего процесса обслуживания. Такая система называется многофазной СМО. Более сложной являются система, имеющая последовательно и параллельно расположенные каналы, и система с сетевой структурой.

Рассмотрим и рассчитаем одноканальную СМО с простейшим входным потоком и экспоненциальным распределением длительности обслуживания. Механизм обслуживания – с ожиданием. Обслуживание осуществляется в порядке поступления заявок в систему. Параметром, характеризующим входной поток, является интенсивность поступления заявок , а параметром, характеризующим канал обслуживания, - интенсивность обслуживания .

Обозначим число находящихся в системе заявок, включая уже обслуживаемые, через n. Это число является дискретной случайной величиной, которая принимает значения:

, (2.37)

где N – максимальное число заявок, характерное для конкретного технологического процесса.

Определим распределение случайной величины (2.37) в момент времени t, т.е. найдем вероятность связанные условием

Рассмотрим интервал времени от t до , где - отрезок времени, в течение которого в очередь поступает не более одной заявки и в канале обслуживается не более одной заявки. Тогда вероятность поступления одной заявки за время по закону Пуассона:

а вероятность обслуживания одной заявки:

где m – число обслуженных заявок на некотором интервале времени.

При малых значениях :

Составим таблицу ситуаций в системе за время (2.2). Рассматривая состояние СМО в момент времени t+ как сложное событие, определяем:

(2.37)

Используя выражение (2.37), находим производную изменения вероятностей во времени:

Таблица 2.2

Номер ситуации	Число заявок в системе в момент t	Число поступивших заявок на время	Число обслуженных заявок за время	Число заявок в системе в момент t+
1	n-1	1	0	n
2	n	0	0	n
3	n	1	1	n
4	n+1	0	1	n

Распределение вероятностей случайной величины получается на основании решения системы дифференциальных уравнений:

Для стационарного режима при В этом случае от системы дифференциальных уравнений переходим к системе алгебраических уравнений:

(2.39)

Вероятности помимо стационарных называют предельными или финальными вероятностями. Если имеет место условие:

(2.40)

где - коэффициент загрузки канала, то стационарные вероятности для системы с ожиданием всегда существуют.

Среднее время ожидания заявки в очереди:

(2.41)

Рассчитаем СМО с приоритетами. Для этих систем характерно, что задержки в обслуживании приводят к определенным потерям, которые зависят от степени важности заявок. Достижение минимальных потерь связано с назначением оптимальных приоритетов для разных заявок. Эта задача включает в себя также установление оптимального характера приоритетов (выбор между относительными, абсолютными и смешанными приоритетами).

При относительных приоритетах появление в очереди заявки более высокого приоритета, чем выполняемая, не прерывает выполнения последней. В момент окончания обслуживания из ожидающих заявок выбирается заявка с самым высоким приоритетом, а если их несколько – то, та, которая поступила раньше.

При абсолютных приоритетах появление заявки более высокого приоритета прерывает обслуживание и реализуется поступившая заявка. В момент освобождения канала обслуживания из ожидающих заявок выбирается заявка с самым высоким приоритетом, а если их несколько – то та, которая поступила раньше. Таким образом, абсолютные приоритеты действуют в двух случаях: при поступлении заявок и при освобождении канала, а относительные только во втором случае.

Возможно введение смешанных приоритетов, занимающих промежуточное положение между абсолютными и относительными приоритетами.

У входной поток с параметрами Длительность обслуживания заявок i-го типа – случайная величина с плотностью распределения математическое ожидание и дисперсию которой обозначим и соответственно. Пусть приоритеты установлены в соответствии с номерами потоков: самый высокий у первого, затем у второго и т.д.

При относительных приоритетах среднее время ожидания заявок типа равно

(2.42)

где - коэффициент загрузки системы всеми заявками от 1-го до го типа включительно:

При абсолютных приоритетах с дообслуживанием прерванной заявки среднее время ожидания начала обслуживания:

. (2.43)

Рассмотрим класс смешанных приоритетов. Условимся, что среди заявок в очереди, обслуживание которых не началось, заявки i-го типа имеют преимущество перед заявками -го типа, если Далее определим интервалы времени таким образом, что если и если Кроме того, Тогда заявка -го типа, до окончания обслуживания которой осталось время (причем преимущество перед заявкой i –го типа, обслуживание которой не началось. Если же то перед ней имеет преимущество любая заявка i-го типа.

Среднее время ожидания рассчитывается по рекуррентному алгоритму:

(2.44)

где

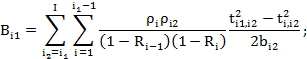
Все слагаемые правой части (2.44) имеют простой физический смысл. Например, первый член – среднее время обслуживания заявок из потоков от 1 до , которые уже находились в очереди на начало обслуживания к моменту поступления рассматриваемой -oй заявки; второй член – среднее время обслуживания всех заявок из потоков от 1 до , поступивших за время ожидания рассматриваемой – й заявкой; третий член – среднее время дообслуживания заявки, находившейся в этот момент в канале, и т.д.

Перейдем теперь к задаче установления оптимальных приоритетов по критерию

(2.45)

где – потери при ожидании обслуживания в относительных единицах.

Условие оптимальности относительных приоритетов:

(2.46)

При абсолютных приоритетах с дообслуживанием прерванной заявки оптимальными являются приоритеты, удовлетворяющие (2.46), если дополнительно выполнены неравенства:

(2.47)

Кроме того, при выполнении неравенств (2.47) оптимальные абсолютные приоритеты лучше по критерию (2.45),чем оптимальные относительные.

Если все неравенства (2.47) не выполнены, то оптимальные относительные приоритеты лучше оптимальных абсолютных. Если же часть этих неравенств выполнена, то соответствующие потоки будут иметь абсолютный приоритет, а остальные - относительный.

Пусть потоки перенумерованы в соответствии с неравенствами (2.46). Значения минимизирующие (2.45), имеют простой вид:

(2.48)

Это эквивалентно правилу выбора заявок на обслуживание: всегда обслуживать ту заявку, у которой отношение минимально. Величина есть время дообслуживания заявки.

Оптимальные смешанные приоритеты лучше по критерию (2.45), чем оптимальные абсолютные и оптимальные относительные.

При исследовании сложных систем и выборе их рациональных режимов функционирования необходимо иметь возможность анализа СМО при различных характеристиках входных потоков и каналов обслуживания, при изменяемых начальных условиях работы системы. В большинстве случаев исследование сложной системы методом натурного эксперимента неприемлемо по затратам и из-за необходимости вмешательства в функционирование. Поэтому широко используется имитационный подход, основанный на статистическом моделировании с применением ЭВМ. Сущность этого подхода состоит в построении для исследуемого процесса моделирующего алгоритма, который позволяет имитировать функционирование элементов сложной системы и взаимодействие между ними с учетом статистических характеристик входного потока и канала обслуживания СМО. Имитационное моделирование позволяет программно изменять значения параметров и начальные условия при автоматизированном исследовании системы. Для моделирования входных потоков и каналов, а также механизма обслуживания используются алгоритмы генерирования случайных последовательностей.

Разработка имитационной модели включает ряд этапов.

1. Содержательное описание технологического процесса как СМО. Определяются возможные законы распределения и параметры входных потоков, каналов обслуживания, процедуры и механизмы обслуживания заявок в СМО. Формируется цель моделирования по отношению к показателям эффективности исследуемой системы.

2. Построение моделирующего алгоритма и структурной схемы имитационного моделирования. Технологический процесс записывается в виде последовательности операторов с указанием связей между ними. В качестве операторов моделирующего алгоритма используются: арифметические операторы логические операторы формирования случайных последовательностей , счетчики операторы ввода-вывода информации

3. Разработка программных средств имитационного моделирования. Моделирующий алгоритм, представленный в виде структурной схемы, реализуется на языке программирования применительно к конкретной ЭВМ.

3. МЕТОДЫ И АЛГОРИТМЫ ОПТИМАЛЬНОГО

ПРОЕКТИРОВАНИЯ

3.1. Классические и численные методы решения

задач оптимизации

Классические методы используются для поиска максимума (минимума) некоторого показателя, когда требования к сложной системе можно выразить в виде функций или функционалов. Основные свойства и условия экстремума функций и функционалов приведены в табл. 3.1.

Таблица 3.1

1. Переменная величина называется функцией переменной x: если каждому значению из некоторой области изменения соответствует значение . Аналогично определяются и функции нескольких переменных.	1. Переменная величина называется функционалом, зависящим от функции если каждой функции из некоторого класса функций соответствует значение Аналогично определяются и функционалы, зависящие от нескольких функций, и функционалы, зависящие от функций нескольких независимых переменных.
2. Приращением аргумента функции называется разность между двумя значениями этой переменной	2. Приращением или вариацией аргумента функционала называется разность между двумя функциями:
3. Линейной функцией называется функция , удовлетворяющая условиям: где произвольная постоянная; Линейная функция одной переменной где постоянная.	3. Линейным функционалом называется функционал удовлетворяющий условиям: где произвольная постоянная;

Продолжение табл. 3.1

	Пример линейного функционала:
4. Дифференциал функции равен	4. Вариация функционала равна
5. Необходимое условие экстремума. Если дифференцируемая функция достигает максимума или минимумаво внутренней точке области определения функции, то в этой точке (3.1)	5. Необходимое условие экстремума. Если функционал имеющий вариацию, достигает максимума или минимума при где внутренняя точка области определения функционала, то при (3.2)

Рассмотрим процесс решения задач оптимизации без ограничений. Задача оптимизации без ограничений обычно представляет собой поиск экстремума функций многих переменных. Для функций многих перемен­ных необходимое условие экстремума (3.1) имеет вид:

, (3.3)

где - обозначение градиента функции, или, переходя к частным производным, имеем систему алгебраических уравнений:

(3.4)

Решение системы (3.4) является оптимальным решением экстремальной задачи без ограничений в случае выполнения достаточных условий экстремума. Поскольку достаточные условия экстремума (максимума):

H

(H - – вещественная симметричная матрица вторых производных функции , вычисленных в точке , в общем случае сложны, на практике, для установления того, что решение системы уравнений (9.4) будет давать максимум, минимум (и что именно) или нет (седлообразная точка), необходимо исследовать функцию при значениях, близких к .

Распространенной задачей оптимизации функционалов является исследование на экстремум

(3.5)

причем граничные точки допустимых кривых фиксированы: и ; функция F(x,y,y^') трижды дифференцируема.

Необходимое условие экстремума функционала (3.5) имеет вид:

(3.6)

где

.

Применяя ряд преобразований к (3.6), получаем необходимое условие в виде уравнения Эйлера:

(3.7)

Интегральные кривые уравнения Эйлера называются экстремалями. Только на экстремалях достигается максимальное или минимальное значение функционала (3.6). Однако для того чтобы установить, реализуется ли на них в действительности экстремум (максимум или минимум), используют следующие достаточные условия экстремума:

1) условие Якоби, которое состоит и том, чтобы решение уравнения:

(3.8)

где

обращалось в нуль в центре х⁰ пучка экстремалей и больше не обращалось в нуль ни в одной точке отрезка х⁰ ≤х≤х₁, на котором задан функционал (3.5);

2) условие Лежандра: для максимума,

для минимума.