3.2.3. Обобщенный метод Фибоначчи

Для устранения недостатка метода дихотомии, связанного с поте­рей информации о проведенных на предыдущем шаге испытани­ях, потребуем, чтобы информация об одном из проведенных на (k – 1)-м шаге испытании или сохранялась с целью ее использования на k-м шаге. Это позволит проводить в те­кущем интервале неопределенности [а_k, b_k] только одно новое ис­пытание. Из рис. 5.3 видно, что для выполнения сформулированно­го условия необходимо, чтобы при точка совпадала с точкой (рис. 3.3, а), а при точка совпадала с точкой (рис. 3.3, б).

В качестве критерия эффективности выбора новой точки испыта­ния, как и в методе дихотомии, будем использовать требование (3.17), чтобы наибольшая длина текущего интервала неопределенно­сти была как можно меньше. Для выполнения этого требования при заданном расположении точки ( ), точку нового испытания ( ) необходимо назначить таким образом, чтобы пара точек располагалась на отрезке эквидистан­тно от обоих его концов, соответственно, в подынтервалах [а_k, (а_k+b_k)/2] и [(а_k+b_k)/2, b_k]:

(3.22)

Условия (3.22) выполняются, если точки испытаний вычисляются по формулам:

(3.23)

, (3.24)

где

0 ≤ t_k ≤ ½ (3.25)

При этом длина интервала неопределенности [а_k+1,b_k+1] не за­висит от вида функции Q(x) и вычисляется по формуле:

b_k+1 – a_k+1 = – a_k = b_k – = (1 – t_k)(b_k – a_k) (3.26)

Можно сказать, что при точка совпадает с точ­кой , а при точка совпадает с точкой , ес­ли коэффициент t_k в формулах (3.23) — (3.24) удовлетворяет соот­ношению:

(3.27)

Из (3.26) следует, что на первом шаге поиска (k = 0) после прове­дения двух испытаний текущий интервал неопределенности [a₁, b₂] имеет длину:

b₁ – a₁ = (1 – t₀) (b₀ – a₀) = 1 – t₀, (3.28)

так как априорный интервал неопределенности [а, b] = [а₀, b₀] явля­ется единичным интервалом [0, 1]. На втором шаге поиска (k = 1), учитывая (3.28) имеем:

b₂ – a₂ = (1 – t₁) (b₁ – a₁) = (1 – t₁)(1 – t₀). (3.29)

Продолжая аналогичным образом, получим, что после проведе­ния N испытаний наибольшая длина апостериорного интервала не­определенности [а_N, b_N] будет иметь следующее значение:

(3.30)

Таким образом, согласно принципу гарантированного результата (3.16) построение наилучшего алгоритма поиска , удовлетво­ряющего введенным выше условиям, сводится к решению экстремальной задачи:

(3.31)

при условии, что

0 ≤ t_k ≤ 1/2; (3.32)

(3.33)

Ограничения типа равенства (3.33) позволяют выразить коэффици­енты t_k через параметр t₀:

(3.34)

Здесь u_k-2, u_k, u_k+2 — числа Фибоначчи, которые задаются с помощью рекуррентного уравнения:

u_k = u_k-1 + u_k-2, k = 2, 3, …

u₀ = u₁ = 1. (3.35)

Аналитическое выражение для N-го числа Фибоначчи задается следующей формулой:

(3.36)

где

При больших значениях N членом в выражении (3.36) можно пренебречь, тогда

(3.37)

Зная аналитические выражения (3.34) для коэффициентов t_k+1 вместо ограничений (3.32) — (3.33) можем записать систему нера­венств, которая после некоторых преобразований примет вид:

0 ≤ t₀ < 1/2; 1/3 < t₀ ≤ 1/2; 1/3 ≤ t₀ < 2/5

u_k+1 / u_k+3 < t₀ ≤ u_k / u_k+2, (3.38)

k = 2, 3, …, N – 1.

Система неравенств (5.30) совместна, если параметр t₀ удовлет­воряет условию:

u_N / _Un+2 < t₀ ≤ u_N-1 / u_N+1 (3.39)

Чтобы выразить наибольшую возможную длину апостериорного интервала неопределенности l_N из (3.30) через параметр (1 – t_k), найдем значения разностей (1 – t_k):

(1 – t₁) = t₀ / (1 – t₀); (1 – t₂) = (1 – 2t₀) / t₀;

(1 – t_k) = – (u_k-1 – u_k+1 t₀) / (u_k-2 – u_k t₀), k = 2, N – 1. (3.40)

Отсюда

(3.41)

Полученное выражение для длины апостериорного интервала не­определенности [а_N, b_N] и неравенство (3.39) позволяют перейти от экстремальной задачи (3.31) — (3.33) к одномерной задаче оптими­зации:

(3.42)

при условии, что

u_N / u_N+2 < t₀ ≤ u_N-1 / u_N+1

Оптимальным решением сформулированной задачи (3.42) является значение параметра , которое определяется по формуле:

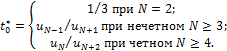(3.43)

Алгоритм , реализующий правило размещения точек ис­пытаний , в текущем интервале неопределенности [a_k, b_k] по формулам (3.23) — (3.24), где коэффициенты t_k вычисляют по соот­ношениям (3.27), использующим оптимальное значение параметра из (3.43), называется методом Фибоначчи. Это название мето­да F₂ возникло в связи с тем, что стратегия поиска точки локального минимума х* унимодальной функции Q(x) связана с использовани­ем чисел Фибоначчи (3.36).

Пусть имеется возможность провести N-нечетное число испыта­ний. На первом этапе, который соответствует первому шагу метода F₂ (k = 1), эквидистантно от концов априорного интервала неопре­деленности [0,1] проводится пара испытаний в точках и , оп­ределяемых N-м и (N-1)-м числами Фибоначчи (рис. 3.5, а).

;

(3.44)

Согласно условию унимодальности функции Q(x) перед вторым этапом происходит сокращение априорного интервала неопределен­ности по информации о ее значениях в точках испытаний и . Если , то а₁ = 0 и b₁ = ; если то и b₁ = 1 (рис. 3.5, б).

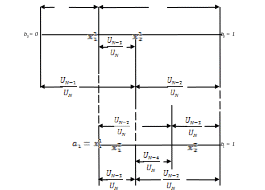
Рис. 3.5. Метод Фибоначчи

Второй этап метода F₂ включает в себя (N-3) итерационных шага (k= 2,3, …, N-3), на каждом из которых точку очередного нового испытания (или ) выбирают таким образом, чтобы пара точек располагались эквидистантно от обоих концов те­кущего интервала неопределенности (рис. 3.5, б).

На третьем этапе после проведения (N-1) испытания определяет­ся, по какую сторону от точки (или ), которая сохраня­ется от предыдущего (N-З)-го шага, лежит точка локального мини­мума х*. С этой целью последнее N-е испытание проводится вбли­зи от точки сохранившегося испытания, например, в точке , где — минимально допустимый сдвиг. При этом пол­учается апостериорный интервал неопределенности [a_N, b_N], дли­на которого при нечетном числе испытаний N имеет следующую оценку:

(3.45)

На рис. 3.6 показана зависимость отношения длин апостериор­ных интервалов неопределенности метода дихотомии (F₁) и метода Фибоначчи (F₂) как функция от числа проведенных испытаний N (при = 0):

(3.46)

Рис. 3.6. Зависимость отношения гарантированных точностей метода дихотомии и метода Фибоначчи от числа проведенных испытаний N при = 0

Из приведенной зависимости видно, что метод Фибоначчи на классе унимодальных функций точнее, чем метод дихотомии. Так, при N = 17, гарантированная точность метода Фибоначчи приблизи­тельно в 8 раз выше, чем гарантированная точность метода дихото­мии.

В табл. 3.3 приведены результаты решения задачи оптимизации:

методом Фибоначчи F₂ для N = 5 и = 0,02.

Таблица 3.3

							Этап
0	–	–	–	–	0	1	–
1	0,375	0,625	–0,09375	0,15625	0	0,625	1
2	0,25	0,375	–0,125	–0,09375	0	0,375	2
3	0,125	0,25	–0,09375	–0,125	0,125	0,375	2
4	0,25	0,27	–0,125	–0,1242	0,125	0,25	3

Апостериорный интервал неопределенности после проведения ис­пытаний имеет длину:

l₅(F₂) = b₅ – a₅ = 0,25 – 0,125 = 0,125,

в то время как гарантированная точность метода Фибоначчи, вы­численная по формуле (3.42), равна 0,1325.

Недостатком метода Фибоначчи является то, что априори необ­ходимо задавать фиксированное число испытаний N, так как на первом этапе требуется вычислить N-e и (N-1)-е числа Фибоначчи для определения параметра .

В связи с этим рассмотрим вновь экстремальную задачу (3.31) — (3.33), но при этом потребуем, чтобы на каждом шаге коэффициен­ты в соотношениях (3.23) — (3.24), связанных с определением па­ры точек испытаний и , сохранялись постоянными:

. (3.47)

Тогда реализация принципа гарантированного результата (3.16) при выполнении условий (3.25), (3.27) и (3.47) сводится к одномер­ной экстремальной задаче следующего вида:

(3.48)

при условии, что

0 ≤ ≤ 1/2; (3.49)

. (3.50)

Из решения уравнения (3.50) получаем:

Однако в силу ограничения (3.44) оптимальным решением зада­чи (3.48) — (3.50) является параметр:

Алгоритм , реализующий правило размещения точек ис­пытаний , в текущем интервале неопределенности [а_k, b_k] по формулам (3.23) — (3.24), где коэффициенты t_k выбирают постоян­ными и равными параметру , называется методом золотого се­чения. Этот метод отличается от метода Фибоначчи только прави­лом проведения первых двух испытаний (рис. 3.7, а):

(3.51)

Рис. 3.7. Метод золотого сечения

В связи с тем, что точка делит апостериорный интервал неоп­ределенности [0,1] на две части таким образом, что отношение дли­ны всего отрезка к большей части равно отношению большей части к меньшей, такое деление называется золотым сечением. Этим и объясняется название алгоритма .

Отметим некоторые свойства метода золотого сечения:

- на каждом k-м шаге поиска точки испытаний , и располага­ются эквидистантно от ближайших к ним концов текущего интерва­ла неопределенности [а_k, b_k]:

(3.52)

- на каждом шаге поиска, кроме первого, испытание проводится только в одной новой точке или ;

- после каждого шага поиска текущий интервал неопределенности уменьшается в раз:

(b_k+1 – a_k+1) = (b_k – a_k); (3.53)

- после проведения N испытаний гарантированная точность опре­деляется следующей оценкой:

l_N(F₃) = b_N – a_N = ^N-1 + ; (3.54)

- при одном и том же числе испытаний N апостериорный интервал неопределенности отличается от апостериорного интервала неопре­деленности, полученного с помощью метода Фибоначчи, только на 17 % ( = 0):

(3.55)

В табл. 3.4 приведены результаты решения задачи оптимизации:

обобщенным методом Фибоначчи при t₁ = ² (реализация метода зо­лотого сечения F₃) для N = 5 и = 0,02

Таблица 3.4

k	x1	х2	x3	x4	Q1 = Q(x3)	Q2 = Q(x4)
1	0	1	0,61803	0,38197	0,14590	-0,09017
2	0	0,61803	0,38197	0,23607	-0,09017	-0,12461
3	0	0,38197	0,23607	0,14590	-0,12461	-0,10333
4	0,38197	0,14590	0,23607	0,29180	-0,12461	-0,12151
5	0,14590	0,29180	0,23607	—	-0,12461	—

Апостериорный интервал неопределенности после проведения пяти испытаний имеет длину:

l₅ (F₃) = b₅ – а₅ = х₂ – х₁ = 0,29180 - 0,14590 = 0,146,

что совпадает с гарантированной точностью метода золотого сече­ния, вычисленной по формуле (3.50). Полученная методом золотого сечения F₃ погрешность превышает погрешность метода Фибоначчи F₂ не более, чем на 17 %:

l_N (F₃) / l_N (F₂) =1,1672.

При больших значениях N метод золотого сечения и метод Фибо­наччи практически начинаются в одних и тех же точках испытаний и . Например, уже при N = 7 имеем u₅/u₇ = 8/21 ≈ 0,381 и ² ≈ 0,382. Этот факт позволяет реализовать алгоритмы F₂ и F₃ в виде единой процедуры (рис. 3.8) — обобщенного метода Фибоначчи при различных значениях параметра t₁:

(3.56)

В качестве условия окончания поиска в обобщенном методе Фи­боначчи (модуль "Поиск закончен" в блок-схеме на рис. 3.8) мо­жет использоваться, например, фиксированное число испытаний N, точность определения погрешности локализации точки локального минимумах и т.д.

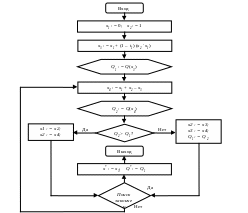
Рис. 3.8. Структурная схема поиска минимума по алгоритму, реализующему обоб­щенный метод Фибоначчи