3.3.3. Методы минимизации квазиньютоновского типа

Рассмотрим класс алгоритмов , которые основаны на квадра­тичной апроксимации минимизируемой функции Q(x) в ∆-окрестности каждого приближения х^k разложением в ряд Тейлора (3.101). В связи с тем, что для определения очередного приращения ∆^k эти алгоритмы требуют вычисления первых и вторых производных функций Q(x), они получили название методов второго порядка.

В том случае, когда гессиан G(x^k) является положительно опреде­ленной матрицей, приращение ∆^k, обеспечивающее наибольшую скорость уменьшения функции Q(x) при постоянном значении квадратичной части разложения в ряд Тейлора, определяется из ре­шения задачи оптимизации:

(3.111)

при условии, что

Построим для сформулированной задачи функций Лагранжа:

Значения ∆ и а должны удовлетворять системе уравнений:

откуда следует, что оптимальным решением задачи (3.111) является вектор:

(3.112)

где (G^–1(х^k) — матрица, обратная гессиану функции Q(x), вычис­ленному в точке х^k.

Алгоритм , основанный на использовании итерационной формулы (3.82), где процедуры выбора длины шага и направления поиска s^k совмещены и сводятся к вычислению приращения ∆^k по формуле (3.112), является реализацией метода Ньютона. Основная идея этого метода заключается в том, что на каждой ите­рации осуществляется выбор приращения А*, соответствующего расстоянию до минимального значения квадратичной формы (3.101), аппроксимирующей нелинейную функцию Q(x) в точке х^k рядом Тейлора (рис. 3.11). При минимизации квадратичной функции Q(x) = x^TGx + b^T х + а, независимо от значения коэффициентов обусловленности матрицы G, метод Ньютона F₁₃ позволяет найти точку локального минимума х* из любого начального приближения х⁰ за одну итерацию.

Недостатком метода Ньютона является требование, чтобы на­чальное приближение х⁰ находилась в достаточно малой окрестно­сти точки локального минимума х*. При выполнении этого требова­ния алгоритм F₁₃ обладает квадратичной скоростью сходимости. Однако на практике это условие часто трудно выполнить, в связи с чем при неудачном начальном приближении х⁰ использование ме­тода Ньютона может привести к расходящемуся процессу.

Для обеспечения сходимости метода Ньютона к точке минимума х* независимо от значения начального приближения х⁰ будем опре­делять приращение ∆^k следующим образом:

(3.113)

где длина шага является оптимальным решением одномерной за­дачи оптимизации:

x₂

(3.114)

Рис. 3.11. Геометрическая интерпретация метода Ньютона с точки зрения квадра­тичной аппроксимации минимизируемой функции Q(x) усеченными рядами Тейло­ра относительно точек испытаний х⁰, х¹, х² (пунктирные линии уровня)

Вместо решения задачи оптимизации (3.114) длину шага можно выбирать из условия:

(3.115)

Для этого на каждой итерации, начиная с значения , умень­шают шаг до тех пор, пока не выполнится неравенство (3.115). Если приближение х^k находится далеко от точки минимума х^k, то дли­ну шага назначают небольшой, при приближении точки х^k к точ­ке х* длина шага будет стремиться к единице.

Алгоритм , основанный на итерационной формуле (3.82), в которой приращение ∆^k определяется выражением (3.113), а длина шага регулируется условием (3.114) или (3.115), называет­ся методом Ньютона с регулируемым шагом.

Общим недостатком алгоритмов F₁₃ и F₁₄ является то, что в них процесс поиска точки минимума х* может расходиться, если гессиан G(x^k) не является положительно определенной матрицей.

Для обеспечения требования, чтобы на каждой итерации гессиан G(x^k) был положительно определенной матрицей, можно использо­вать следующий прием:

(3.116)

где Е — единичная матрица; — достаточно большое положитель­ное число.

Тогда существует ортогональная матрица V такая, что

V^TG(x^k) V = V^TG(x^k)V + E = Д(x^k) + E, (3.117)

где Д(x^k) — диагональная матрица, элементы d_ii(x^k) которой рав­ны собственным значениям гессиана G(x^k). Из соотношения пол­учаем:

(Д(x^k) + E)^–1 = 1 / (d_ii(x^k)+ ). (3.118)

Следовательно, использование в выражении (3.118) значения:

(3.119)

позволяет уничтожить отрицательные собственные значения в пре­образованной матрице . Однако при слишком больших значе­ниях может оказаться, что тогда процесс поиска точ­ки минимума х* по алгоритму F₁₃ (или F_l4) приближается к процес­су поиска по методу наискорейшего спуска F₁₀ со всеми его недо­статками.

В связи со сказанным выше выбор параметра будем осуществ­лять путем решения следующей одномерной задачи оптимизации:

(3.120)

при условии, что

Необходимым условием существования оптимального решения для задачи оптимизации (3.120) является неравенство нулю первой производной от минимизируемой функции по :

Нетрудно видеть, что

Следовательно, оптимальное значение параметра , является решением уравнения:

(3.121)

Алгоритм , в котором используется преобразованная матрица и параметр выбирают из решения уравнения (3.121), реализует модифицированный метод Ньюто­на. Процедура поиска точки минимума х* по алгоритму F₁₅ сво­дится к следующей последовательности действий.

1. На первой итерации (k = 0) для заданного начального прибли­жения х⁰ вычисляют значение градиента и гессиана G(x⁰) минимизируемой функции Q(x).

2. Определяют точку очередного испытания

где — оптимальное решение одномерной задачи оптимизации

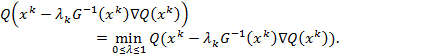
3. Если выполняется неравенство

Q(x^{k + 1}) < Q(x^k),

то в точке х^{к + 1} вычисляют градиент и гессиан G(x^k), принимают: k := k + 1 и все вычисления повторяют с шага 2. В противном случае , переходят к шагу 4.

4. Гессиан G(x^k) преобразуют в матрицу

где — решение уравнения:

5. Определяют точку очередного испытания:

где — оптимальное решение одномерной задачи оптимизации:

6. Поиск точки локального минимума х* заканчивается, если вы­полняется условие . В противном случае все вычис­ления повторяют с шага 2.

Общим недостатком алгоритмов, реализующих различные моди­фикации метода Ньютона является то, что в них требуется вычис­лять матрицу вторых производных G(x^k) и осуществлять обращение этой матрицы G^-1(x^k). В связи с этим рассмотрим класс алгоритмов , не требующих вычисления матриц G(x^k) и G^-1(x^k). Алгоритмы этого класса основаны на формировании специальным образом по­следовательности матриц (H₀, H₁, …, H_k). Эта последовательность обладает тем свойством, что каждый элемент матрицы Н_k аппрок­симирует на k-м шаге соответствующий элемент матрицы G^-1(x^k), но вычисляется только на основании информации о значениях пер­вых производных функции Q(x).

Как было показано, для квадратичной функции Q(x) = x^TGx + b^Tх + а метод Ньютона позволяет получить точку минимума х* из любого начального приближения, например, х^{k + 1} и х^k, за одну ите­рацию:

Откуда получаем равенство, характерное для метода Ньютона:

∆^k = x^{k + 1} – x^k = G^–1y_k , (3.122)

где

В дальнейшем потребуем, чтобы для любой матрицы H₁, …, H_k, получаемой из рекуррентного соотношения:

H_{k + 1} = H_k + ∆H_k, k = 0, 1, 2, … (3.123)

выполнялось условие, называемое квазиньютоновским уравнением:

∆^k = H_{k + 1}У_k (3.124)

или, учитывая соотношение (3.123), вместо соотношения (3.124) пол­учаем равенство

(3.125)

где

Гессиан квадратичной функции является симметричной матри­цей (G = G^T), поэтому потребуем, чтобы каждая из матриц Н_k так­же была симметричной. Чтобы сохранить это свойство у матрицы Н_k+1, необходимо, чтобы для поправки ∆Н_k выполнялось условие:

(3.126)

Класс алгоритмов , в которых направление поиска на каждой итерации определяется с помощью выражения

(3.127)

где матрица Н_k удовлетворяет условиям (3.123) — (3.126), получил на­звание квазиньютоновских методов минимизации.

В связи с тем, что матрица ∆Н_k, удовлетворяющая условиям (3.125) — (3.126), является не единственной, будем определять значе­ния ее элементов из решения следующей задачи оптимизации:

(3.128)

при условии, что

∆H_ky_k = ∆^k – H_ky_k = (3.129)

∆H_k = ∆ (3.130)

где Ф(∆Н) — сумма квадратов диагональных элементов матрицы ∆Н;

Т_r (∆Н, ∆Н^T) — след (трек) матрицы (∆H, ∆H^Т);

.

Можно показать, что оптимальное решение задачи (3.128) — (3.130) получают с помощью следующего выражения:

В зависимости от вида матрицы П из выражения (3.131) могут быть получены различные модификации квазиньютоновских методов минимизации, принадлежащих классу алгоритмов .

В том случае, когда матрица П является единичной (П = Е), для поправки ∆Н_k получаем выражение:

(3.132)

Если матрица П совпадает с текущим значением матрицы H_k, аппроксимирующей матрицу G^–1 на k-м шаге (П = H_k), то для по­правки ∆H_k получаем выражение:

(3.133)

Широко известной является поправка ∆H_k, используемая в ал­горитме Давидона-Флетчера-Пауэла :

(3.134)

Теоретическое сравнение методов сопряженных направлений и квазиньютоновских методов минимизации показывает, что при ми­нимизации квадратичных функций они полностью совпадают. При минимизации нелинейных функций Q(x) квазиньютоновские мето­ды оказываются предпочтительнее, если "дно оврага" функции Q(x) не очень извилистое. Однако программная реализация квазиньюто­новских методов требует больших затрат оперативной памяти, чем при реализации методов сопряженных направлений.