3.3. Методы безусловной оптимизации

3.3.1. Методы многопараметрического поиска без вычисления производных

При решении задачи параметрической оптимизации часто при­ходится иметь дело с математическими моделями, в которых не имеется аналитических выражений для первых производных мини­мизируемого критерия оптимальности Q(x). В связи с чем поиск оп­тимального решения х* приходится вести только по испытаниям, связанным с получением численного значения многопараметриче­ской функции Q(x₁,…,x_n). Алгоритмы, которые используют для вы­бора точки очередного испытания х^k информацию только о значе­нии функции Q(x), принадлежат классу методов пря­мого поиска (методов минимизации без вычис­ления производных; методов нулевого порядка).

Наиболее простыми из алгоритмов данного класса являются алгоритмы, реализующие идею покоординатного спуска, которая заключается в том, что поиск точки локального минимума х* сво­дится к поочередному изменению переменных вдоль одной из коор­динатных осей:

(3.57)

где , — i-й координатный n-мерный вектор с компонентами:

Длина шага вдоль i-й координатной оси (направления поиска, определяемого i-м координатным вектором l_i) может выбираться равной некоторой постоянной величине , по следующему правилу:

(3.58)

Если окажется, что для всех , то длина пробных ша­гов должна быть уменьшена ( ) и поиско­вые движения с новым значением шага должны быть повторены по всем координатным направлениям , . Поиск считается за­конченным при выполнении условия:

(3.59)

Алгоритм реализующий описанную стратегию поиска точки минимума х*, называется методом покоординатного спуска с постоянным шагом.

В том случае, когда длина шага на каждой итерации (3.57) оп­ределяется с помощью решения одним из методов унимодального поиска одномерной задачи оптимизации:

(3.60)

приходим к алгоритму , реализующему релаксационный метод Гаусса—Зейделя, процедура поиска точки минимума х*, в котором сводится к следующей последовательности действий.

1. Задается начальное приближение х^k = х⁰.

2. Осуществляется циклический покоординатный спуск из точки х^k по итерационной формуле (3.57) с выбором длины поискового ша­га из условия (3.60) для всех i от 1 до n. Эта процедура образует внутренний цикл, в процессе которого осуществляется одномерная минимизация функции Q(x_i, ..., x_n) по каждой переменной х_i.

(3.61)

3. После окончания внутреннего цикла в качестве нового началь­ного приближения х^k принимается точка хⁿ, полученная после ре­шения n-й задачи оптимизации (3.61), и все вычисления повторяют­ся с шага 2.

4. Поиск точки минимума х* считается законченным, если после очередного внутреннего цикла выполняется условие:

(3.62)

Геометрической интерпретацией траектории поиска, которая получается по алгоритмам F₅ и F₆, является ломаная, состоящая из отрезков прямых, которые параллельны осям координат.

Недостатком методов покоординатного спуска является то, что при минимизации функций Q(x), имеющих овраг, дно которого не ориентировано вдоль какой-то из координатных осей, процесс по­иска сильно замедляется и может остановиться далеко от точки ис­тинного локального минимума х*.

Отмеченный выше недостаток алгоритмов F₅ и F₆ устранен в ал­горитме , реализующем метод конфигураций, который по­зволяет эффективно осуществлять поиск, минимума многопара­метрической функции Q(x) вдоль произвольно ориентированных относительно координатных осей "прямолинейных" оврагов.

Процесс поиска начинается из начального приближения х⁰, кото­рое принимают за базовую точку х^k, характеризующуюся тем, что она является исходной точкой очередной итерации. Каждая итера­ция состоит из двух этапов: "пробного движения" в ∆-окрестности текущей точки испытания и "движения в допустимом направле­нии", т.е. в направлении вдоль которого гарантируется уменьшение функции Q(x).

Этап "пробного движения" заключается в обследовании ∆-окрестности базовой точки х^k с целью определения допустимого (в смыс­ле уменьшения значения функции Q(x)) направления s^k. Для этого в циклическом порядке, начиная с i=1, по итерационной формуле (3.57) изменяется каждая переменная x_i, , где размер шага вдоль координатного направления l_i выбирают из условия (3.58). При этом начальный размер пробного шага ∆_i для каждой из перемен­ных может иметь различные значения. Если полученное значение не равно нулю, то при выполнении пробного движения вдоль (i+1)-го координатного направления в качестве значения Q(x^k) рассматривается либо (если ), либо (если ). После просмотра всех координатных направ­лений l_i, , получается точка , в которой значение функции Q(x) меньше или равно значению функции в базовой точке Q(x^k):

(3.63)

Если окажется, что = , т.е. ведличина принятого пробного шага ∆ настолько велика, что не позволяет определить допустимое направление, то необходимо его уменьшить и повторить все пробные движения заново. Таким образом, по мере приближения к точке минимума х* длина пробных шагов уменьша­ется. Поиск считают законченным, если для пробных шагов ∆_i = 1, выполняется условие (3.59).

В случае выполнения неравенства (3.63) для в качестве допустимого направления s^k выбирают вектор ( ), который указывает направление уменьшения функции Q(x) вдоль дна ее "прямолинейного" оврага. Периодическое повторение пробных дви­жений позволяет подстраивать траекторию поиска вдоль дна оврага в тех случаях, когда установленное на предыдущей k-й итерации допустимое направление s^k оказывается неудачным (в смысле уменьшения функции Q(x) на (k+1)-й итерации.

Этап "движения в заданном направлении" сводится к следующей последовательности действий.

Вдоль направления s^k определяется точка по формуле:

(3.64)

где h > 1 — шаг вдоль допустимого направления.

Например, при h = 2 получаем:

(3.65)

После каждого i-огo шага (i = 1,2,3,...) вдоль допустимого направ­ления относительно текущей точки проводят процедуру "пробного движения", цель которой — определить, не нуждается ли допустимое направление s^k в коррекции. Если после проведения n пробных движений полученная точка не совпадает с базовой точкой ( ), то в качестве скорректированного до­пустимого направления выбирают вектор ( ), вдоль ко­торого и делается очередная итерация с шагом h:

, (3.66)

где — "удачная" точка, определенная вдоль допустимого на­правления s^k. Если точка лежит на одной прямой с точками х^k и , то направление поиска s^k сохраняется (не корректируется). В обоих случаях вычисление функции Q(x) вдоль допустимого на­правления продолжается до тех пор, пока в очередных точках испы­таний получаются уменьшающиеся значения функции Q(x). Когда в допустимом направлении не удается найти точку ис­пытания с меньшим значением функции Q(x), то поиск в направлении s^k считают законченным и переходят снова к первому этапу. В этом случае точку предыдущего "удачного" испытания выбирают в качестве базовой точки для (k+1)-й итерации, из которой проводятся пробные движения с целью определения нового допустимого направления s^k+1.

Недостатком алгоритма F₇ является то, что в процессе проведе­ния пробных движений направление вдоль дна оврага может быть пропущено, так как пробные движения делаются только параллель­но координатным направлениям l_i, . По этой же причине по­иск может "остановиться" на дне оврага вдали от точки истинного минимума х*.

Для устранения отмеченного недостатка метода конфигураций в алгоритме , реализующем метод вращающихся коорди­нат, предлагается вместо того, чтобы изменять каждую перемен­ную x_i, независимо параллельно координатной оси, осущест­влять на k-й итерации преобразование системы координат (х) та­ким образом, чтобы в новой системе координат ( ) одна из осей сов­падала с направлением вдоль дна оврага функции Q(x), а остальные оси были к ней ортогональны. После проведения последовательно вдоль каждого из n взаимноортогональных направлений одномерного унимодального поиска минимального значения функ­ции Q(x) строится новая система координат и так до тех пор, пока точка минимума х* не будет локализована с заданной точностью .

Первая итерация в алгоритме F₈ полностью совпадает с процеду­рой поиска по релаксационному методу Гаусса-Зейделя F₆. Вдоль координатных направлений l_i, поочередно решается одно­мерная задача оптимизации (3.60). На последующих итерациях од­номерная задача оптимизации решается для каждого линейно-неза­висимого взаимноортогонального направления . Начиная с базовой точки х^k, определяют шаг вдоль направления , при котором достигается минимальное значение функции Q(x):

(3.67)

Затем, начиная с точки , определяют шаг вдоль направле­ния , при котором достигается минимальное значение функции Q(x):

(3.68)

После проведения одномерного поиска по всем n направлениям ( вместо начального приближения х^k получается новая точка , которая может быть охарактеризована совокупностью ве­личин ( ).

Обозначим через вектор перехода из точки х^k в точку , че­рез — вектор перехода из в и т.д. Тогда система линей­но-независимых векторов , может быть записана следую­щим образом:

…………………..

или в общем виде

(3.69)

Вектор представляет собой допустимое направле­ние из базовой точки х^k вдоль дна оврага. В связи с этим в качестве нового направления (первого направления поиска в следую­щей итерации) примем вектор :

(3.70)

где — норма вектора в евклидовом пространстве.

Для получения направ­лений поиска ( ) ортогональных направлению и взаимноортогональных между собой применим процедуру ортогонализации Грамма-Шмидта:

(3.71)

; (3.72)

Полученную с помощью этой процедуры систему векторов , принимают на очередной (k+1)-й итерации за новые направ­ления поиска, вдоль которых поочередно решаются одномерные за­дачи оптимизации типа (3.67) — (3.68).

При построении взаимно ортогональных направлений , по формулам (3.70) — (3.72) необходимо, чтобы ни один из коэффициентов , не равнялся нулю. Для устранения этого недостатка преобразуем выражения (3.70) — (3.72) таким образом, чтобы значения коэффициентов , , не влияли на процедуру построения новой системы координат , . С этой целью бу­дем строить векторы и их модули таким образом, чтобы они были пропорциональны коэффициенту . Тогда при вы­числении направления , величины сокра­тятся и направление можно будет определить даже в том слу­чае, если .

В связи с тем, что направление совпадает с вектором можно записать .

Так как векторы являются единичными, получаем:

направление определяем так:

(3.73)

Из выражения (3.73) следует , если один или несколько коэффициентов равны нулю при условии, что . Рассуждая аналогичным образом, для последующих k = 2,3,..., n получаем выражения:

, (3.74)

(3.75)

. (3.76)

Если , то при условии, что . В частном случае для i = n из выражения (3.76) получаем

. (3.77)

Из (3.77) следует, что если , при и при имеем для .

Таким образом, выражения (3.73) — (3.77) позволяют определить взаимно ортогональные направления , образующие но­вую систему координат, если один и более их коэффициентов равны нулю при условии, что для . В противном случае (при условии, что ) будем считать, что i-е направление поиска остается без изменения:

.

Рассмотрим алгоритм , реализующий метод сопряжен­ных направлений нулевого порядка, в котором в отличие от метода вращающихся координат F₈, одномерный унимодальный поиск про­водится не вдоль ортогональных, а вдоль сопряженных направле­ний.

Пусть минимизируется квадратичная функция Q(x) с положи­тельно определенной матрицей G(x^T G_x > 0):

. (3.78)

Тогда, если точка x' является точкой минимума квадратичной функции Q(x) вдоль направления , а точка х" — точкой миниму­ма этой же функции, полученной из другой начальной точки вдоль направления, параллельного направлению , то вектор (х" - х') яв­ляется G -сопряженным с направлением :

. (3.79)

Геометрический смысл этого свойства квадратичной функции Q(x) заключается в том, что если точки минимума х' и x распо­ложены на двух параллельных направлениях, то истинный мини­мум х* функции Q(x) следует искать вдоль направления (х'' - х'). При этом прямая (х'' - х'), проходящая через точку минимума х*, будет пересекать поверхности постоянного уровня квадратичной функции (Q(x) = const) под равными углами (рис. 3.9).

Рис. 3.9. Геометрическая интерпретация G-сопряженности направлений и (х'' - х') при минимизации квадратичной функции Q(х) = x^TGx + (b^T, х) + а

Обобщая полученный результат на случай нескольких ненуле­вых сопряженных направлений для квадратичной функции получаем, что, если, начиная с точки х^k, по всем направ­лениям находятся точки минимума функции Q(x) (причем точка является точкой минимума вдоль последнего r-го направления ) то вектор будет G-сопряжен по всем r на­правлениям :

(3.80)

В случае квадратичной функции Q(x) построенное таким образом направление поиска оказывается сопряженным на­правлениям относительно гессиана G(x^k).

Рассмотренный способ построения сопряженных направлений по­зволяет описать алгоритм F₉ в виде следующей последовательности действий.

1. Задают начальное приближение х°, которое принимают за ба­зовую точку для k-й итерации (k=1): х^k = х°.

2. Направления поиска выбирают равными линейно-не­зависимым координатным векторам l_i,:

3. Для всех i от 1 до n вдоль каждого направления решают од­номерную задачу оптимизации:

Эта процедура позволяет получить траекторию поиска, которая заканчивается в точке:

4. Определяют направление , вдоль которого реша­ют одномерную задачу оптимизации:

5. Строят новую совокупность текущих направлений поиска:

6. В качестве базовой точки х^{k + 1} следующего (k+1)-го итераци­онного шага выбирают точку 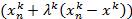все вычисления повторяют с шага 3.

7. Поиск заканчивается при выполнении условия:

Можно показать, что поиск точки минимума х* квадратичной функции Q(x) с помощью метода сопряженных направлений нуле­вого порядка заканчивается не более чем за n итераций, т.е. алго­ритм F₉ обладает квадратичной скоростью сходимости.