Глава 1. Задачи механики
Механика – раздел физики, в котором изучается механическое движение, т.е. перемещение одних тел или частей тела относительно других.
Задача механики состоит в экспериментальном исследовании различных движений и обобщении полученных экспериментальных данных в виде законов движения, на основании которых далее в каждом конкретном случае может быть предсказан характер возникающего движения.
Раздел механики, в котором рассматриваются только методы описания движений, но не ставятся вопросы о законах движения, называются кинематикой.
Законы движения и их применение к отдельным конкретным задачам изучает динамика, которая в виде частного случая включает в себя статику, изучающую условия, при которых тела остаются в покое. В зависимости от характера изучаемых движений, свойств тел и содержания вопросов, на которые должен быть получен ответ, механика делится на:
механику точки;
механику твердых (недеформируемых) тел;
механику упругих тел, включающую в себя механику жидкости и газов
Рассмотрим следующий пример:
Металлический диск подвешен горизонтально на цилиндрической пружине, прикрепленной к центру диска (рис. 1, а).
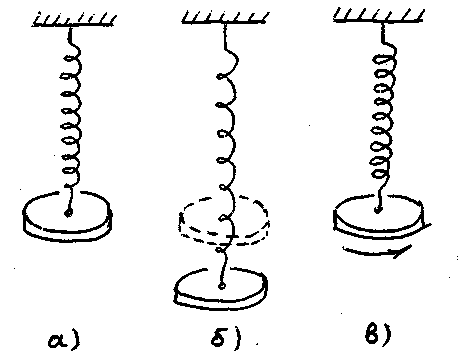
Рис.1
Когда диск совершает вертикальные колебания, которые возникают, например, если мы оттянем диск вниз и сразу отпустим его (рис. 1, б), то период колебаний не зависит сколько-нибудь заметно от размеров и форм диска, а определяется упругостью пружины и массой диска.
Когда диск совершает крутильные колебания вокруг вертикальной оси, которые возникают, например, если мы повернем диск вокруг вертикальной оси на некоторый угол, а затем сразу отпустим его (рис. 1, в), то опыт показывает, что период колебаний диска, помимо упругих свойств пружины, зависит от размеров, формы и массы диска, но не зависит от его упругих свойств.
Если же нас будет интересовать вопрос о периоде тех звуковых колебаний, которые будет совершать диск после удара по нему, то мы на опыте сможем убедиться, что период этих колебаний зависит не только от массы, размеров и формы диска, но и от его упругости.
Таким образом, опыт показывает, что в разных движениях определяющую играют разные свойства реального объекта.
Период времени колебаний диска зависит (помимо упругих свойств пружины) от его массы, но не зависит от его размеров и упругих свойств. Поэтому можно заменить диск материальной точкой, т.е. телом, не обладающим размерами, но обладающим массой. Тем самым мы правильно отразим то единственное свойство реального объекта, которое играет определяющую роль в рассматриваемом движении.
Период крутильных колебаний зависит от массы диска и его размеров, но не зависти от его упругих свойств; поэтому рассматривая диск или твердое тело, мы сможем правильно отразить те свойства реального диска, которые играют роль в рассматриваемом движении.
Период звуковых колебаний зависит не только от размеров диска, но и от упругих свойств и плотности материала, из которого диск сделан. Поэтому только представление об упругом теле, обладающем размерами, упругостью и плотностью реального диска позволяет правильно отразить его свойства, которые играют роль в рассматриваемом движении.
В природе не существует ни материальных точек, ни твердых (недеформируемых) тел, ни абсолютно упругих тел. Всё это абстракции, которыми приходится пользоваться в науке для правильного отражения тех свойств реальных объектов, которые необходимо учесть при решении поставленной задачи. Применяемые абстракции никогда не отражают полностью всех свойств реального объекта. Однако это и не важно, если те свойства реального объекта, которые применяемая абстракция не отражает, не сказываются сколько-нибудь заметно на характере изучаемого движения, между тем применение абстракций существенно упрощает решение всякой задачи.