Учебное пособие 2003

Следовательно,

F(х2,у2)=P(х1≤X<x2; у1≤Y<у2)+F(х1,у2)+F(х2,у1)-F(х1,у1).

Отсюда следует свойство 4.

5. Докажем первое из соотношений пятого свойства. Запишем событие (X<х) следующим образом:

X x X x, k Y k 1 .

k

Поскольку события под знаком суммы попарно несовместны, то в силу ζ-аддитивности вероятности

9.3. Дискретный двумерный случайный вектор

Двумерный случайный вектор (Х,Y) называется дискретным, если каждая его компонента является дискретной случайной величиной.

Множество всех возможных значений G случайного вектора не более чем счетно.

Законом распределения дискретного случайного вектора называется перечень всех возможных значений пар компонент

все возможные значения индексов i и j.

Закон распределения двумерного случайного вектора часто задается таблицей вида

81

Зная закон распределения двумерного случайного вектора, можно получить закон распределения его компонент

где множество индексов U определяется следующим образом:

U={(i,j)|(X<xi, Y<yj)}.

Пример. Задано распределение вероятностей дискретной двумерной CB таблицей

9.4. Непрерывный двумерный случайный вектор

Двумерный случайный вектор (Х,Y) называется непрерывным случайным вектором, если функция распределения F(x,y) непрерывна на всей плоскости и

82

существует такая неотрицательная интегрируемая по Риману в бесконечных пределах по каждой из координат функция f(х,у), называемая плотностью распределения вероятностей случайного вектора (Х,Y), что

Таким образом, плотности распределения вероятностей отдельных компонент случайного вектора выражаются в виде интегралов от совместной плотности распределения.

Свойство 5. Если (Х,Y) - двумерный случайный вектор непрерывного типа, то вероятность попадания случайной точки в произвольную квадратируемую область D R определяется по формуле

D

В самом деле; если D представляет собой произвольный

83

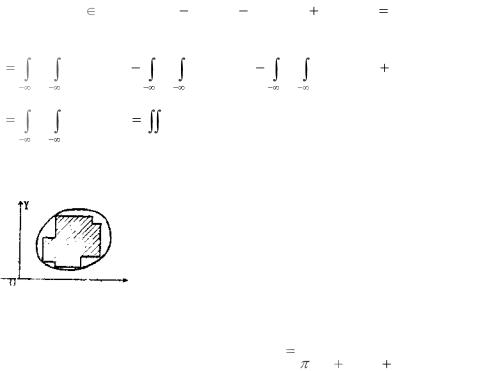
прямоугольник П={x1≤X≤х2, у1≤Y≤y2}, то формула (2) есть очевидное следствие свойства 4 двумерной ФР и определения плотности распределения.

Доказательство для прямоугольной области:

Найти величину a, ФР, вероятность попадания случайной точки (х,у) в квадрат 0≤x≤1, 0≤y≤1.

Предлагается решить самостоятельно.

9.5. Независимость случайных величин

Важнейшее понятие теории вероятностей - независимость событий - сохраняет свое значение и для n- мерных случайных величин.

84

СВ X1, Х2,..., Хп называются независимыми (в совокупности), если для любых событий {Xk Вk}, k=1, 2,..., п, где В1, В2, Bn – подмножества числовой прямой, имеет место

то есть n-мерная ФР равна произведению одномерных

ФР.

Оказывается, что это соотношение (4) имеет место и в общем случае, то есть справедлива следующая теорема.

Теорема. СB X1, Х2,..., Хп независимы тогда и только тогда, когда в любой точке х=(x1, x2,..., хп) Rn имеет место равенство (4). В чаcтноcти, для двух СB (X,Y) имеем

F(x,y)=F(x)·F(y). (5)

Доказательство теоремы проведем для случая двух СВ. За B1 и В2 выберем любые полуинтервалы чиcловой прямой, то есть

В1=[х1; х2[, В2=[у1; у2[ .

Достаточность. Пусть выполнено условие (5), тогда по свойству 4 двумерной ФР

P(x1≤Х<x2, у1≤Y<у2)=F(x2,y2)-F(x1,y2)-F(x2,y1)+F(x1,y1)= =F(x2)F(y2)-F(x1)F(y2)-F(x2)F(y1)+F(x1)F(y1)=F(x2)·[F(y2)-F(y1)]-

-F(x1)· [F(y2)-F(y1)]= P(x1≤Х<x2)·P(у1≤Y≤у2).

Необходимость. Пусть выполняется условие (3) определения, которое для двух CВ при таким образом

что при учете произвольного выбора х2, у2 и приводит к равенству (5).

Замечание. В связи с равносильностью условий (3) и (4) часто за определение независимости СВ принимается условие

(4). Из рассмотренной теоремы, в частности, следует утверждение.

Утверждение. Пусть f(x,y) - плотность распределения двумерной непрерывной СВ (Х,Y). СВ X, Y независимы тогда и только тогда, когда во всех точках непрерывности функции

продифференцировать дважды по переменным х и у соотношение (5).

Для двумерной дискретной СB (Х,Y) из определения независимости (3) следует следующее утверждение.

Утверждение. Для того, чтобы дискретные случайные величины Х,Y были независимы, необходимо и достаточно выполнение равенства

P(X=хi,Y=yj)=Р(Х=xi)·P(Y=yj). (8)

Действительно. Пусть x1<x2<…<xi< - значения, принимаемые СВ X, и y1<y2<…<yj< - значения, принимаемые

СВ Y. Тогда Р(xi≤X<xi+1)=Р(Х=xi) и Р(yj≤Y<yj+1)=Р(Y=yj), i,j=1,2… Подставляя эти выражения в (6), получаем (8). И

наоборот, исходя из (8) легко получить (6).

Ранее (см. свойство 5 двумерной ФР) было доказано, что многомерное распределение определяет одномерные. В общем случае по одномерным распределениям СВ, X1, Х2,…, Хп нельзя восстановить многомерное распределение, однако, если СВ X1, Х2,…, Хп независимы, то по одномерным распределениям можно найти совместное распределение этих СВ, пользуясь формулами (4), (7), (8).

Пример (задача Бюффона). На плоскость, разлинованную параллельными прямыми, отстоящими друг от

86

друга на расстоянии L, наугад бросается "игла" - отрезок длиной l, l≤L. Какова вероятность того, что брошенная игла пересечет одну из линий?

Решение. Обозначим черев θ угол наклона иглы к направлению линий, х - расстояние от нижнего конца иглы до ближайшей сверху линии. Условия опыта таковы, что СВ Ф равномерно распределена на отрезке [0; π], a СВ X - на отрезке [0; L]. Будем считать, что Ф и X независимы. Тогда плотность их совместного распределения

f , x 1 L1 .

Событие - игла пересечет одну из линий - наступает тогда и только тогда, когда х≤l·sinθ, то есть когда соответствующая точка попадает в область D прямоугольника П={0≤θ≤π, 0≤х≤L}, ограниченную кривой х=l·sinθ. Поэтому

x≤l∙sin

87

10. ДИСПЕРСИЯ СУММЫ СЛУЧАЙНЫХ ВЕЛИЧИН. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНОГО ВЕКТОРА. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОГО ВЕКТОРА. ЭЛЛИПС РАССЕИВАНИЯ.

10.1. Дисперсия суммы случайных величин

Если СВ Х и Y независимы, то D(X+Y)=D(X)+D(Y). Используя определение дисперсии и свойство

линейности математического ожидания, получаем

D(X+Y)=M[(X+Y)-M(X+Y)]2=M[(X-M(X))+(Y-M(Y))]2= =M(X-M(X))2+2M[(X-M(Y)(Y-M(Y))]+M(Y-M(Y))2.

Учитывая, что

M[(X-M(X))(Y-M(Y))]=M(X-M(X))M(Y-M(Y))=

=(M(X)-M(X))(M(Y)-M(Y))=0

по свойству 4 получаем

M(X-M(X))2+M(Y-M(Y))2=D(X)+D(Y).

Это свойство по индукции распространяется на сумму п независимых СВ. Если Х1, Х2,…, Хп независимы, то

D(Х1,+Х2 +…+Хп)=D(X1)+D(X2)+…+D(Xn).

Пример. СВ μ - число успехов в п испытаниях Бернулли - имеет биномиальное распределение. Запишем μ как сумму индикаторов

μ=χА1+χА2+…+χАп.

Индикаторы χАi независимы в силу независимости испытаний. Тогда

D(μ)=D(χА1+χА2+…+χАп)=D(χА1)+D(χА2)+…+D(χАп).

для дисперсии

D(μ)=npq.

10.2. Математическое ожидание и дисперсия случайного вектора

Математическим ожиданием n-мерного случайного вектора X=(X1, Х2,..., Хп) называется вектор

88

М(Х)=(М(Х1), М(Х2),..., М(Хп)),

составленный из математических ожиданий координат. Дисперсией n-мерного случайного вектора X=(X1, Х2,...,

Хп) называется вектор

D(X)=(D(X1),D(X2),... ,D(Xn)),

составленный из дисперсий координат.

Математическое ожидание и дисперсия координат вычисляются по формулам, которые мы запишем для случая

п=2.

Если (X,Y) - дискретный случайный вектор, то

10.3. Ковариация. Коэффициент корреляции

Важной характеристикой двумерной (n-мерной) СВ является ковариация (матрица ковариации, или дисперсионная матрица).

Ковариацией (корреляционным моментом) СВ X и Y

называется число, определяемое формулой cov(X,Y)=M[(X-M(X))(Y-M(Y))]. (1)

Из определения ковариации и свойства линейности МО следует, что

cov(X,Y)=M[(X-M(Х))(Y-M(Y))]=М[XY-ХМ(Y)- -YМ(X)+M(X)M(Y)]=M(XY)-M(X)M(Y). (2)

Рассмотрим свойства ковариации.

Свойство 1. Если X и Y - независимые СВ, то cov(X,Y)=0. Следует из (2). Свойство 1 дает достаточный признак зависимости СВ X и Y.

89

Свойство 2. cov(X,X)=D(X), cov(Y,Y)=D(Y). Следует из определения ковариации и дисперсии.

Свойство 3. cov(X,Y)= cov(Y,X).

Свойство 4. cov(с1X+c2Y,Z)=с1сov(X,Z)+с2cov(Y,Z), где c1 и с2 - постоянные. Свойство 4 следует из определения ковариации и свойства линейности МО.

С ковариацией СВ X и Y может быть связана матрица

которая называется матрицей ковариации. Очевидно, что она симметричная.

Если X=(Х1, Х2,..., Хп) - n-мерный случайный вектор, то для него также может быть записана матрица ковариации, которая имеет матричные элементы ζij, определяемые равенствами

ζij=cov(Xi, Xj)=M[(Xi-M(Xi))(Xj-М(Хj))]=М(ХiХj)-M(Xi)M(Xj).

Отсюда видно, что ζij=ζji , то есть матрица ковариации симметричная.

Используя ковариацию, можно получить формулу для дисперсии линейной комбинации двух (и нескольких) СВ без предположения их независимости.

Утверждение. Если для СВ X и Y существует cov(X,Y), то при любых с1, и с2 существует

2c1c2cov X,Y .

Для п-мерного случайного вектора формула (3) принимает вид

90